1-5.対頂角の定理
ユークリッドの原論:線分の扱い
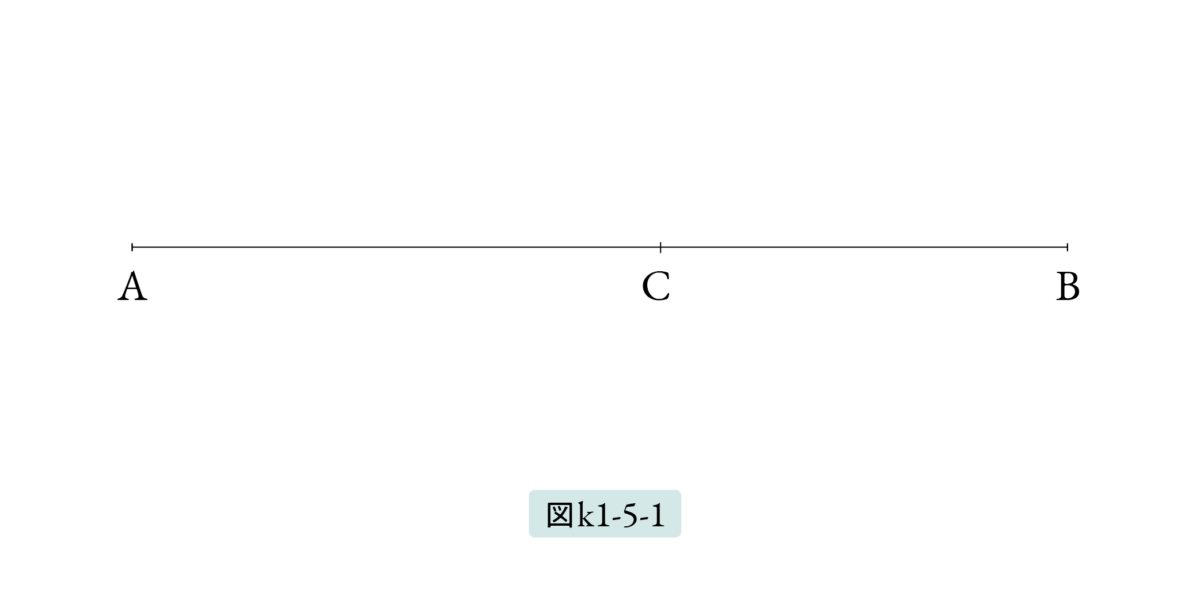
線分 AB 上に点 C を取ります。図K1-5-1。すると線分 AC は線分 AB の部分なので、公理 8 より 線分AB は線分 ACより大きい、AC < AB、となります。また、線分 AC に線分 CB をつないでできる線分 AC+CB は線分 AB とぴったり重なるので、AB = AC + CB となります。
ユークリッドの原論:角度の扱い
原論では角度を数値で表すことがありませんが、読者の皆さんは1周360°の角度をよく知っていると思いますから、以下では説明のためこれを用いることもあります。
O, A, B を直線上にない3点とします。線分 OA と OB からなる図形を角AOB といい ∠AOB と書きます。原論では2直角 (180°)とか4直角 (360°)といった特別な角度を角度として認めていませんが、本連載ではこれらも角度として認めることにします。
また、角はなにも言わなければ、2直角より小さいとします。したがって、∠AOB といった場合、角は一意的に定まります。2直角よりも大きい角も考慮する場合は、2直角より小さい角を劣角、2直角より大きい角を優角と呼びます。

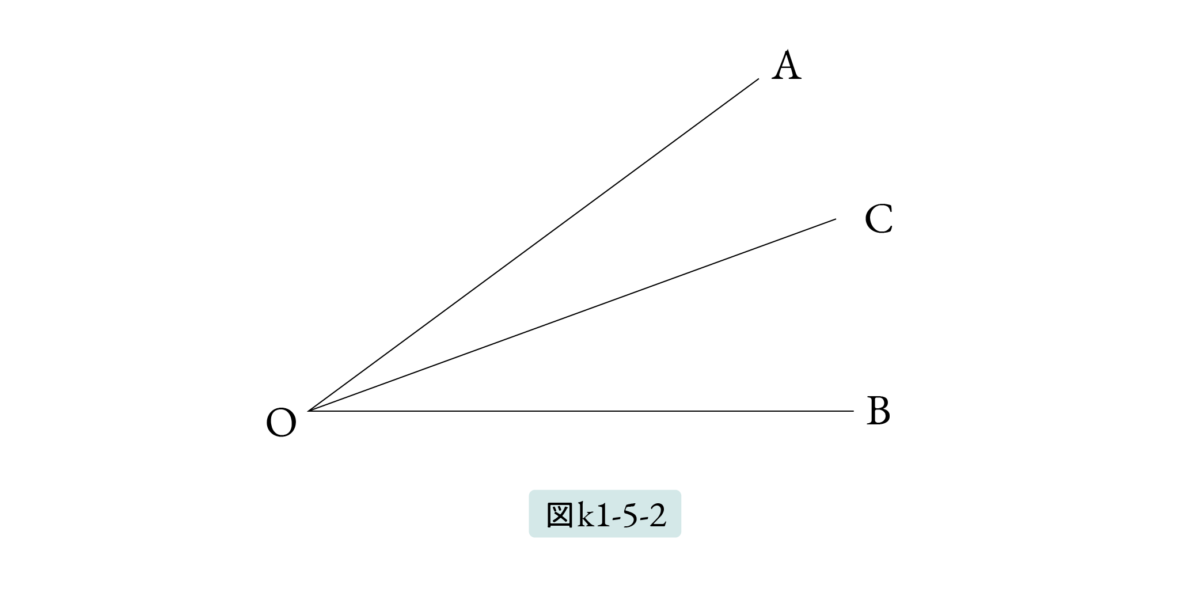
図K1-5-2をみてください。 ∠COB は ∠AOB の部分です。したがって、∠COB < ∠AOB となります。また ∠COB に ∠AOC を加えると ∠AOB と重なり合いますから
∠COB + ∠AOC = ∠AOB
となります。
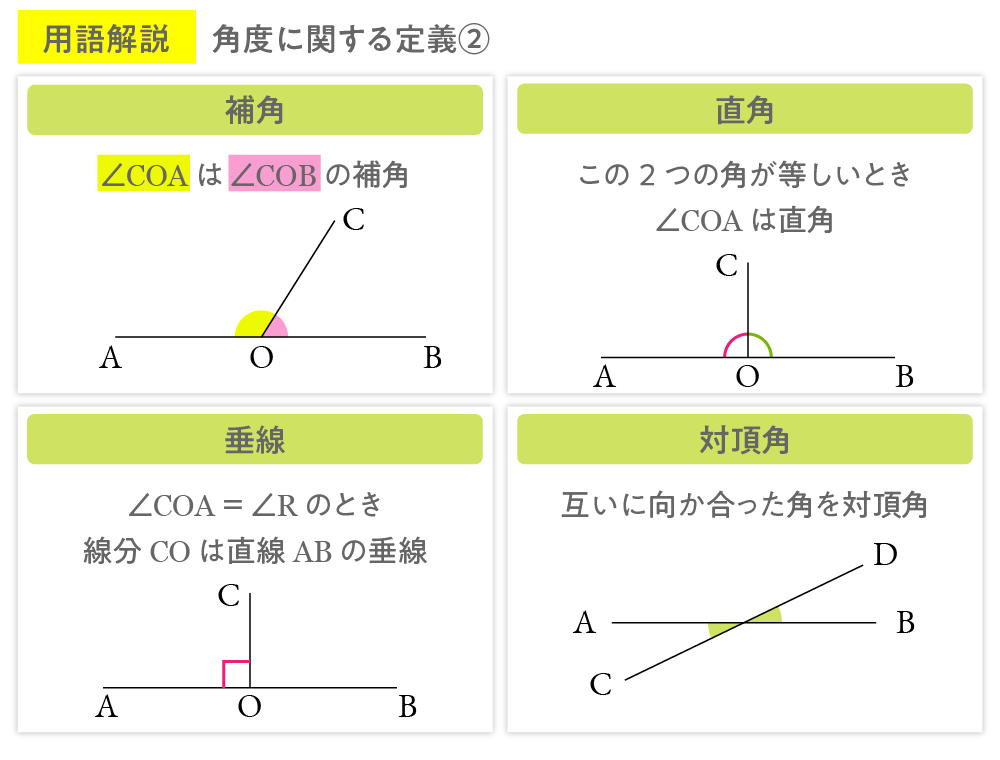
O を直線 AB 上の点、C をこの直線上にない点とします。下の図の『補角』を参照してください。このとき ∠COA は ∠COB の補角であるといいます。この2つの角が等しいとき、∠COA は直角であるといいます。角はその補角と等しいとき直角といいます。直角を∠R で、2直角を 2∠R で表します。
O を直線 AB 上の点、C をこの直線上にない点とします。∠COA = ∠R のとき、線分 CO を直線 AB の垂線、点 O を C からAB に下ろした垂線の足といいます。
ユークリッドの原論『命題 I.13』の証明
原論では次の命題を証明しています。
もし直線上に立てられた半直線が2つの角を作るなら、それらは2つの直角か、あるいはその和は2直角になる。
命題につけられた記号I.13 は、これが『原論』の第I巻の13番目の命題であることを示しています。『原論』の巻の番号は算用数字 1, 2, … ではなく、ローマ数字 I, II, … が用いられ、『原論』の命題は「命題 I.13」のように引用するのが慣例となっています。
さて、命題 I.13を現代風に式で表しましょう。P を直線AB 上の点とし、PC を半直線とします。このとき、次が成立することを示せばよいわけです。
∠APC + ∠CPB = 2∠R
皆さんはこれを証明できますか。「あたりまえすぎて、証明できない」と思っているかもしれませんね。『原論』では次のように証明しています。
証明
∠APC = ∠CPB なら、定義より、∠APC と ∠CPB は直角です。
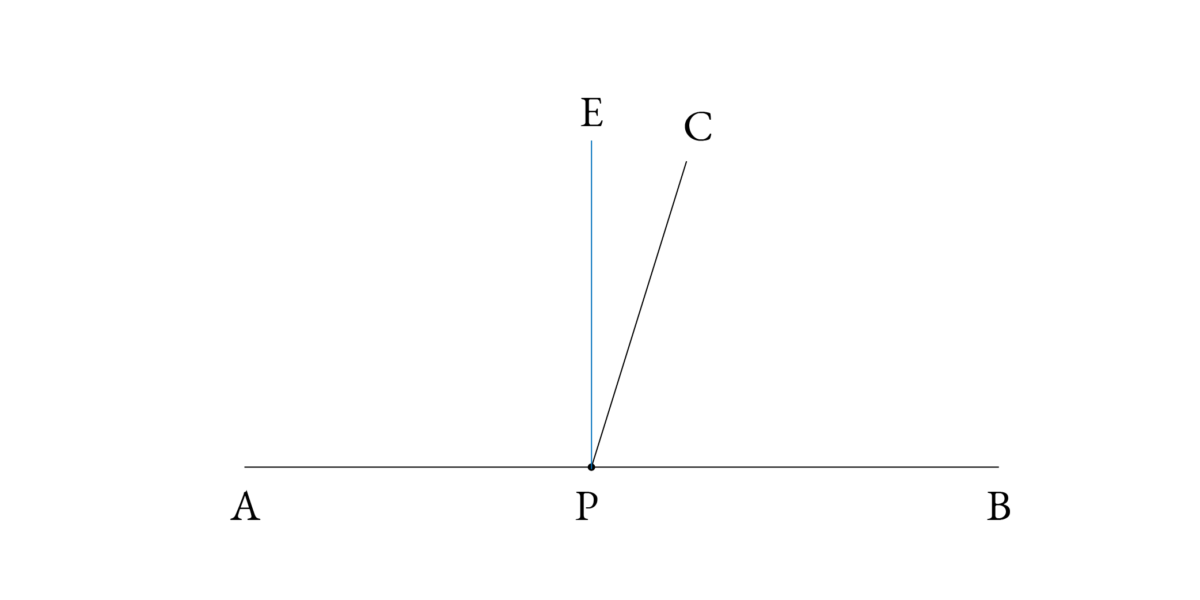
∠APC > ∠CPB としましょう。点 P に AB の垂線 EP を立てます。すると、
∠APC + ∠CPB = (∠APE + ∠EPC) + ∠CPB
= ∠APE +(∠EPC + ∠CPB)
= ∠APE + ∠EPB = 2∠R
となります。
∠APC ≠ ∠CPB とする。∠CPB < ∠APC の場合。∠APC ≦ ∠R とすると、2つの角の和が2直角であることに矛盾する。よって ∠R = ∠APE < ∠APC となる。
ユークリッドの原論:対頂角の定理
図k1-5-3のように2つの直線 ABとCDが点Oで交わっているとします。このとき、互いに向き合った角を対頂角といいます。図K1-5-3ではaとc が、またbとdがそれぞれ対頂角です。
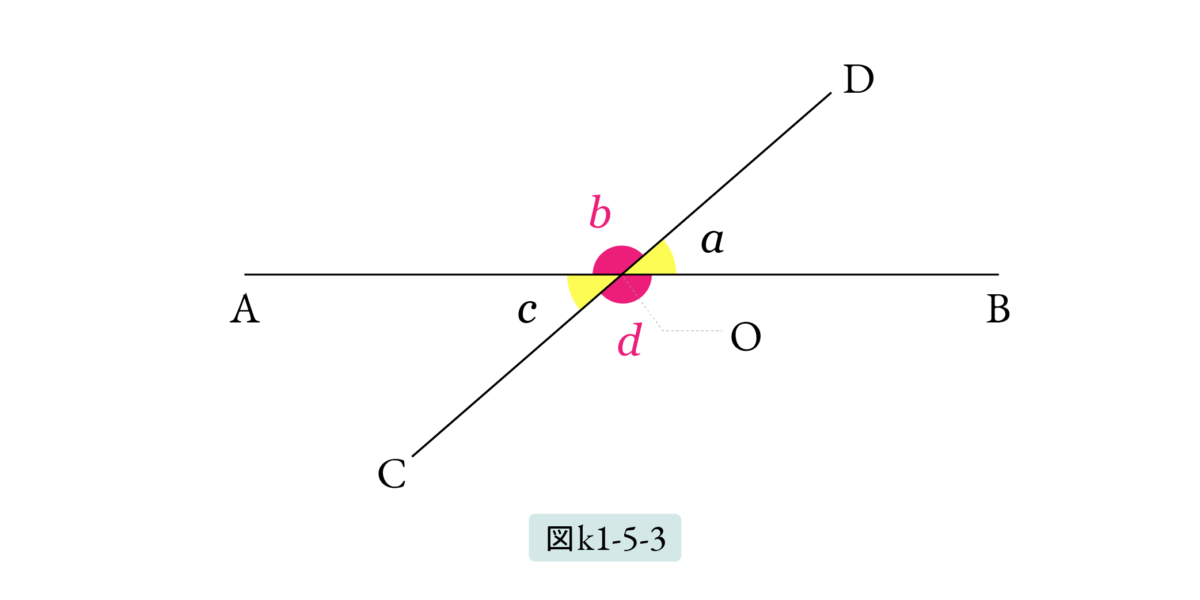
次も原論に出てくるので、命題I.15と書いてもよいのですが、よく知られた定理であり、わざわざ原論を引用することもありません。古代ではパピルスはとても高価だったので、命題は口伝で伝えられるように簡潔に表現されていたようです。現代の数学の著作は機械的に定理に番号をふって「定理 xxx」と書くのですが、ここでは各定理に適当な名前を付けることにします。例えば次では、定理〔対頂角〕と書くことにし、引用するときは対頂角の定理 と書きます。
証明
∠COB = a, ∠AOC = b, ∠DOA = c とおきます図13-8参照。すると命題I.13より
a + b = 2∠R
b + c = 2∠R
が成り立ちます。したがって、
a + b = c + b
が成立します。よって公理3 より、a = c が成立します。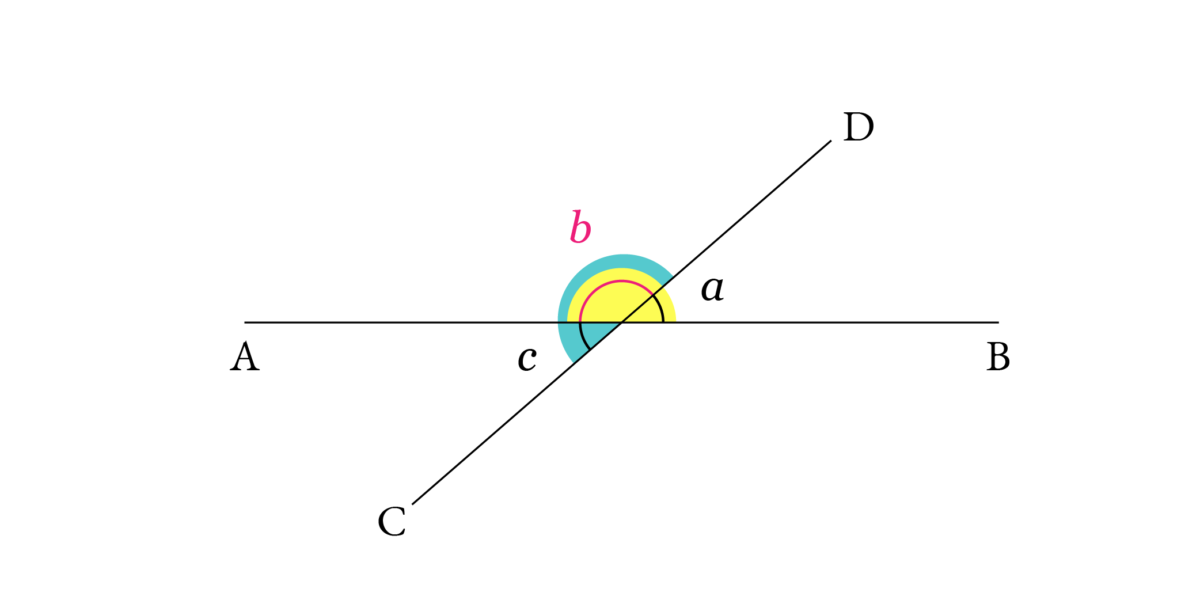
まとめ
今回はユークリッドの原論の命題I.13と対頂角の定理の証明をみてみました。原論では角度は直角を基準に理論が展開されています。原論では概念をひとつずつ丁寧に定義し、理論を組み立てていきます。
