ピタゴラスの定理 とは
ページ目次
ピタゴラスの定理(三平方の定理)とは?
ピタゴラスの定理は三平方の定理とも呼ばれ、直角三角形の性質を表す定理として広く知られています。直角三角形において、直角をはさむ2辺の長さをa,b、斜辺の長さをcとすると、a2 + b2 = c2 が成立します。

逆に三角形の3辺の長さa, b, cの間にa2 + b2 = c2 が成り立てば、その三角形は長さcの辺を斜辺とする直角三角形になります。
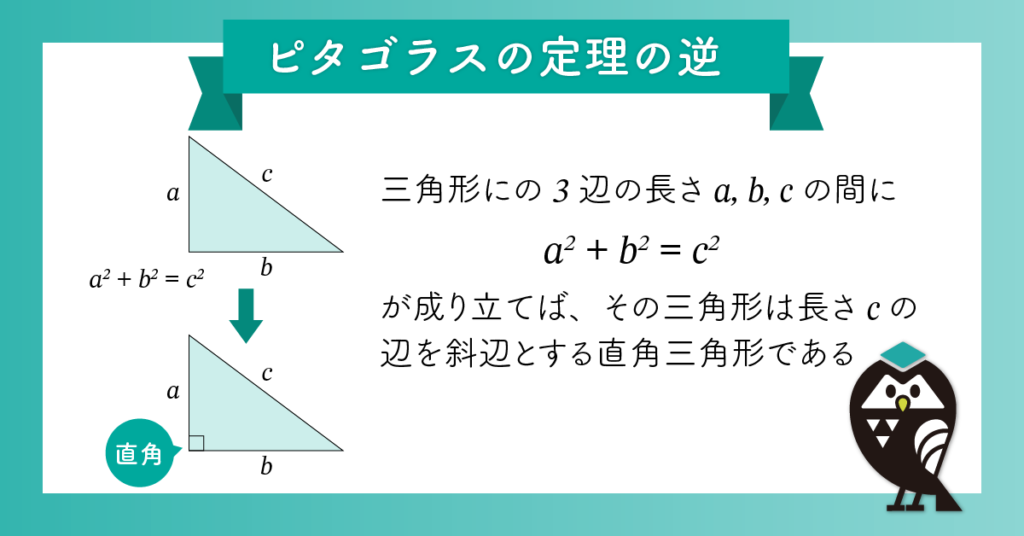
ピタゴラスの定理は次のように説明することができます。「直角三角形において、斜辺上の正方形は、直角をはさむ2 辺上の正方形の和に等しい」

--Advertising--
ピタゴラスの定理の証明
ピタゴラスの定理には数多くの証明があることで有名です。ここではその一つを紹介しましょう。
下の図を見てください。1辺がcの正方形のまわりに、底辺が b 高さが a の直角三角形を4つかきます。すると外側に辺がa+bの正方形ができます。
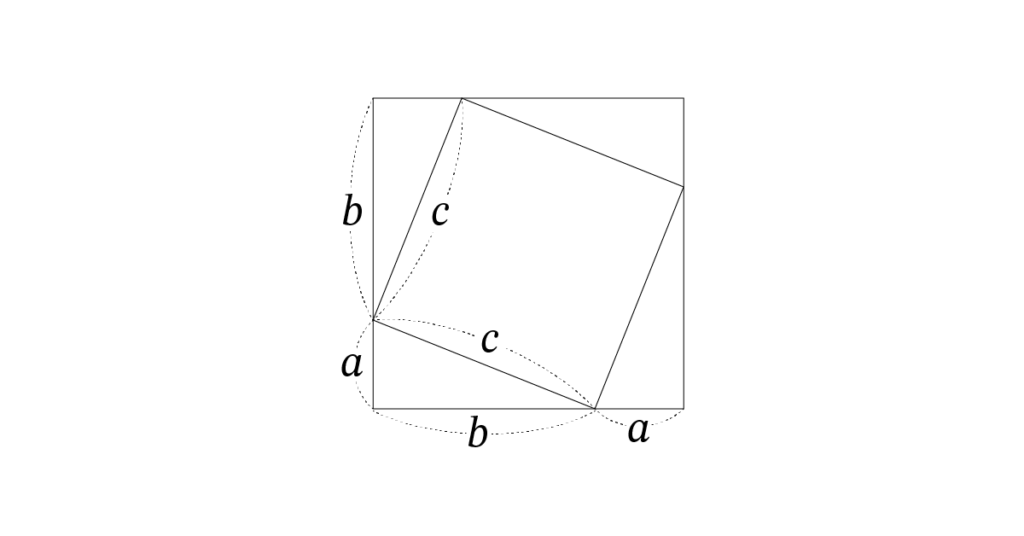
この図で外側の大きい正方形は、1辺がcの正方形と底辺が b 高さが a の直角三角形4つで構成されています。
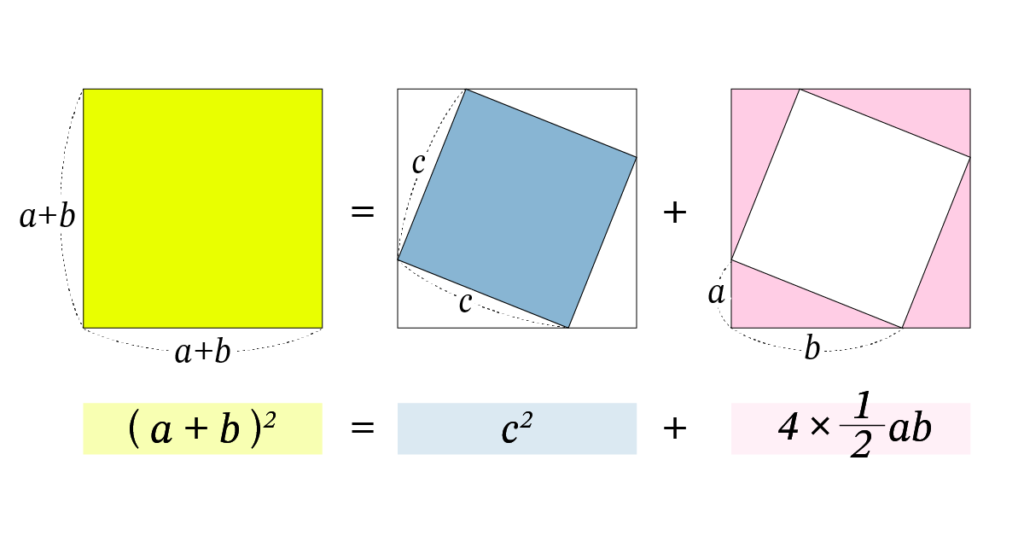
外側の大きい正方形(黄色)の面積は1辺がa+bの正方形なので( a + b )2 です。これは1辺がcの正方形(青色)と底辺が b 高さが a の直角三角形4つ(ピンク)の和なので c2 + 4 × ab/2となります。よって
( a+ b )2 = c2 + 4 × 1/2 ×ab
a2 + 2ab + b2 = c2 + 2ab
a2 + b2 = c2
となり、ピタゴラスの定理が証明されました。
ピタゴラスの3つ組 — 345
「c2 = a2 + b2」を満たす3つの自然数 a, b, c をピタゴラスの3つ組といいます。(a, b, c) がピタゴラスの3つ組なら、(a, b, c) を3辺とする三角形は直角三角形となります。もっとも小さいピタゴラスの3つ組は (3, 4, 5) でこれを元祖ピタゴラスの3つ組と呼ぶ人もいます。
以下はピタゴラスの3つ組です。
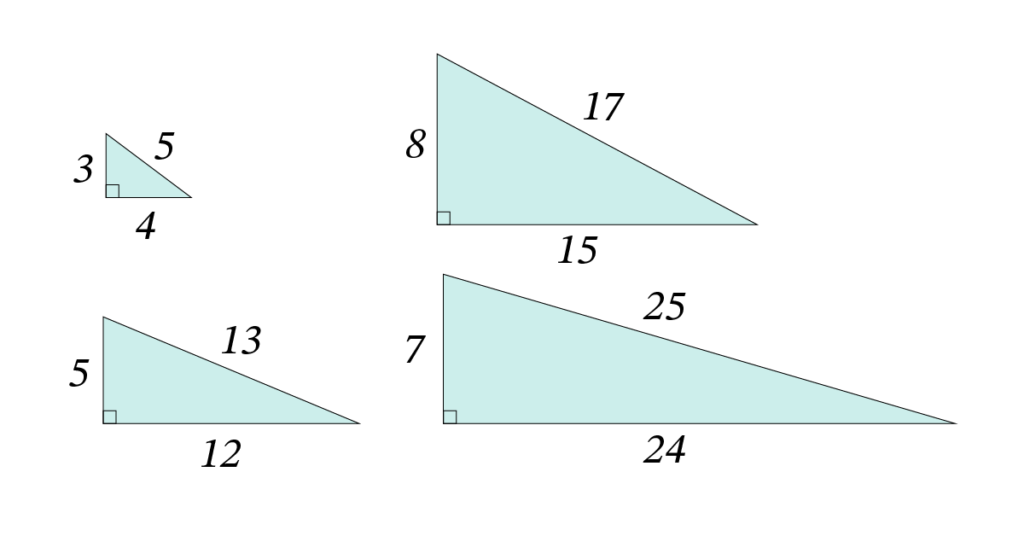
--Advertising--
ピタゴラスの定理の歴史
直角三角形の性質は古代エジプトの時代から使われていました。
エジプト文明はナイル川によって発展しました。ナイル川は、毎年決まった時期に洪水を起こし、上流から農作物の生育に必要な肥沃な土壌を運び、ゆっくりと水位を下げていきます。
ナイル川の水が引くと、あたり一面は泥の海で誰がどこを耕作地とするかが分からなくなってしまいます。しかし心配することはありません。土地は国家が管理していたのです。「縄師」と呼ばれる役人が、大規模な測量をし、国全体の耕作地を区画整理して、農民一人一人の持ち分を割り当てたのです。
土地を農地として切り分けるには“直角”が必要となります。長い一本のロープを、長さ 3, 4, 5 に分け、分け目に印をつけます。このロープで三角形を作り、印のところでピーンと張ると直角三角形ができます。
このように直角三角形の性質は土地の測量に用いられていました。古代エジプト人がピタゴラスの定理を知っていたという証拠は見つかっていません。しかし、(3, 4, 5) がピタゴラスの三つ組であること、つまり 32 + 42 = 52 となることは分かっていました。
名前の由来となったピタゴラスとは?
古代ギリシアの数学者、哲学者として知られているピタゴラス。ピタゴラスは、数には神秘的な力があると信じ、この世界は数によって支配されていると考えていました。ピタゴラスには様々な逸話が残されています。詳しく知りたい方はぜひ以下をご一読ください▼
関連記事以下の記事で詳しく解説しています++。
関連記事以下の記事で詳しく解説しています++。
--Advertising--
「美しい証明」ユークリッドの原論より
古代ギリシアのユークリッドの著書『原論』にあるピタゴラスの定理の証明はとても美しいことで有名です。この証明の動画解説はこちらから▼
動画でわかる数学の定理「ピタゴラスの定理 美しい証明」
ギリシア数学とピタゴラスの定理
現代の私たちは、長さ、面積、体積、角度などを数で表しています。古代ギリシア人も私たちと同様だと思いがちですが、実はそうではありません。古代ギリシア人にとって数とは個数を表わす自然数だけだったのです。〔Web連載ピラミッドの謎:4-2.ピタゴラスの定理〕ではピタゴラスの定理を古代ギリシアの概念だけを使って考えます。
関連記事以下の記事で詳しく解説しています++。




