
フィボナッチ数列とは?〜自然界にも存在する不思議な数列〜
自然界にも現れる不思議な数列「フィボナッチ数列」
花びらの数、貝殻の渦、ウサギの繁殖
一見無関係に見えるこれらの現象の背後に、共通する法則が隠されています。
この記事では、数学史でも有名なフィボナッチ数列とは何か、その規則性や自然界との関係、そして黄金比とのつながりまで、わかりやすく解説します。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
この数字の並びに、何か規則があることに気づいたでしょうか?これは「フィボナッチ数列」と呼ばれる有名な数列で、前の2つの数を足すことで次の数ができるというシンプルな規則に従っています。
フィボナッチ数列は、自然界や芸術作品の中にも見られることで知られており、中学・高校の数学や入試問題にもたびたび登場します。
数字の美しさと不思議さが詰まったこの数列について、詳しく見ていきましょう。
ページ目次
フィボナッチ数列の規則とは?
フィボナッチ数列とは、次のように並ぶ数の列のことです。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
この数列には、「前の2つの数を足すと次の数になる」というシンプルな規則があります。
たとえば:
- 1 + 1 = 2
- 1 + 2 = 3
- 2 + 3 = 5
- 3 + 5 = 8
…というように、数列が次々と生成されていきます。
このルールに従って数を並べていくと、自然とフィボナッチ数列ができあがります。身の回りの自然やアートにも現れる、不思議で美しい数列です

フィボナッチ数列の名の由来
〜ピサのレオナルドとはどんな人物?〜
フィボナッチ数列という名前は、中世イタリアの数学者フィボナッチ(ピサのレオナルド)に由来しています。
彼は商人であった父の仕事の関係で若い頃に東地中海沿岸を訪れ、そこで当時最先端だったアラビア数学を学びました。西暦1200年ごろにピサに戻った後、学んだ知識をまとめて著書として発表します。
この中に登場するのが、のちに「フィボナッチ数列」と呼ばれることになる数列です。もともとの問題は、古代インドのサンスクリット語の詩に由来するといわれています。
しかし、この数列が注目されるようになるのはずっと後のこと。
19世紀になってから、フランスの数学者エドゥアール・リュカがこの数列に「フィボナッチ数列」という名前を付け、本格的な数学研究の対象となりました。
ウサギの問題:1年後に何つがいになる?
フィボナッチが著した書物には、数列の例として次のようなお話が登場します。
ある日、農夫が1つがい(オス1匹・メス1匹)の子ウサギをもらいました。
このウサギたちは次のような習性をもっています:
- 子ウサギは1ヶ月で大人に成長します
- 2ヶ月目から、毎月1つがいの子ウサギを生みます
- 生まれた子ウサギもまた、1ヶ月後には成長して繁殖を始めます
さて、この条件でウサギを飼い始めたら、1年後には何つがいになるでしょうか?
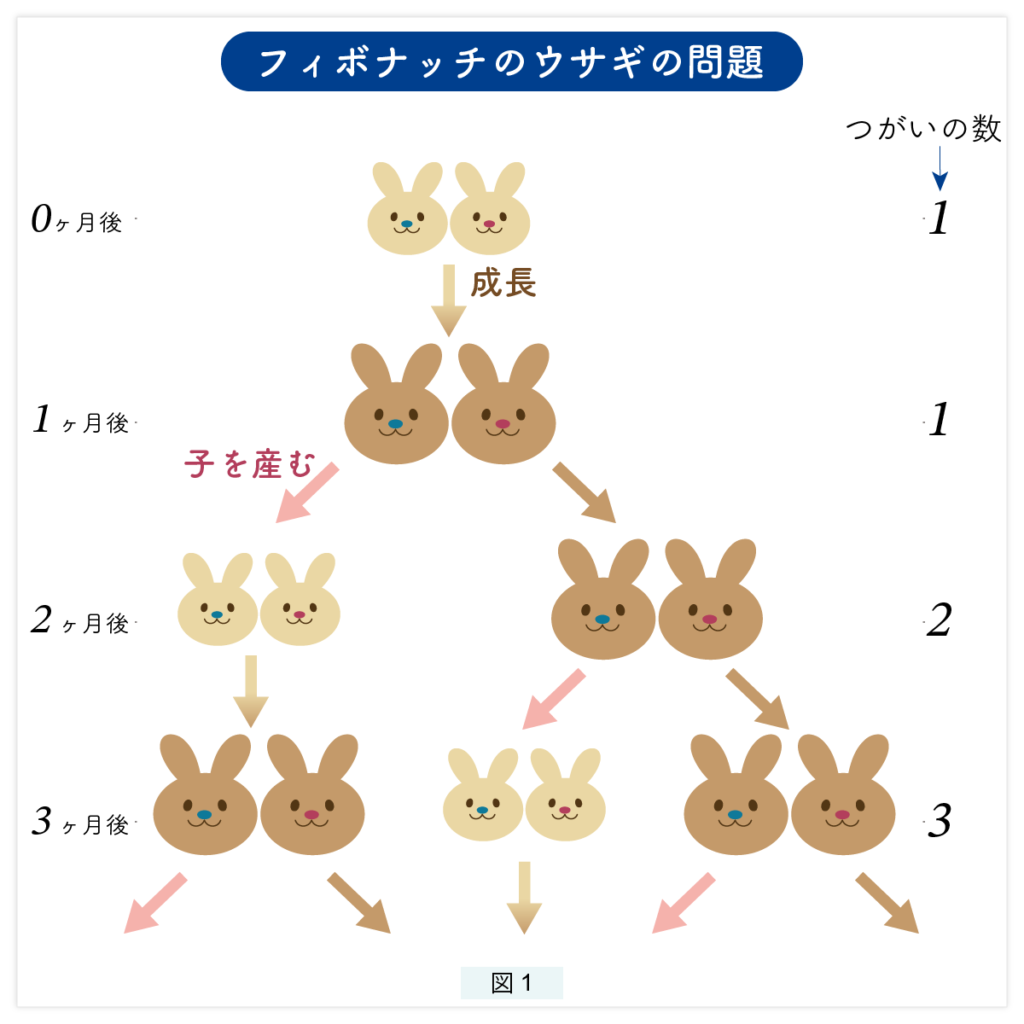
この問題を月ごとに追っていくと、1、1、2、3、5、8…と、フィボナッチ数列が自然に生まれてきます。(図1)
このように、フィボナッチ数列は単なる数学の話にとどまらず、実際の自然現象や成長のパターンを表現するモデルとしても用いられているのです。
フィボナッチの木とは?
図2に示した木の構造は、「フィボナッチの木」と呼ばれています。
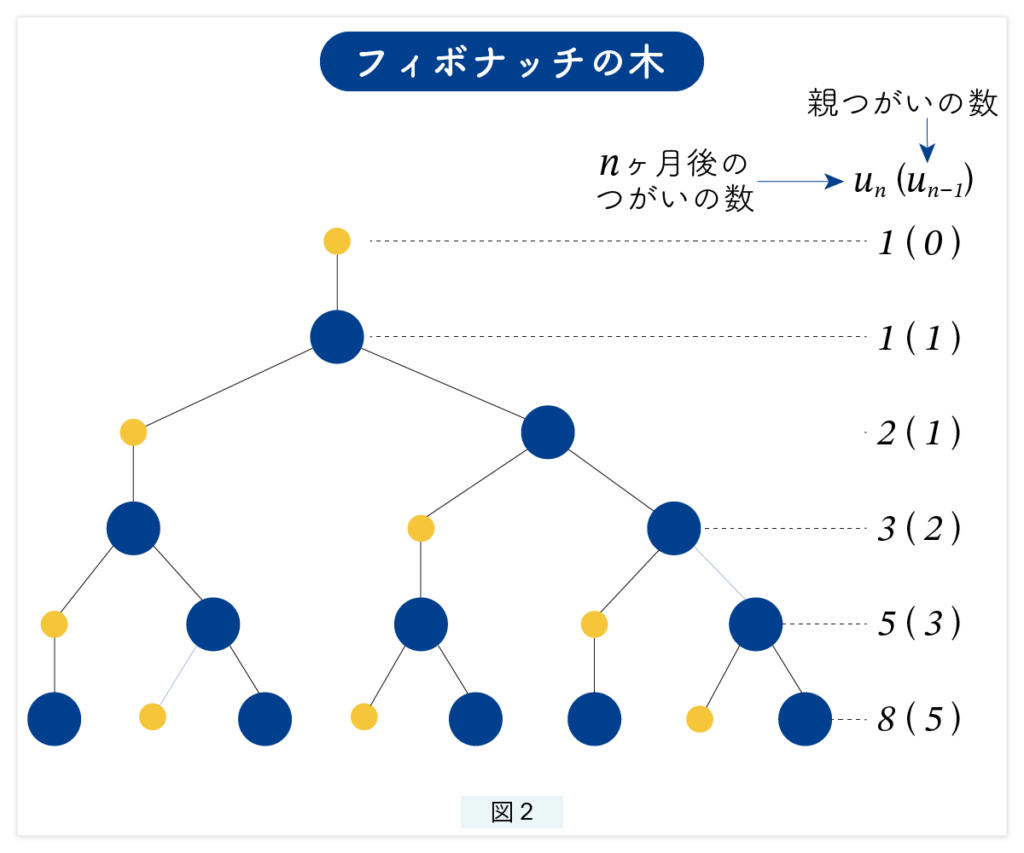
この図では:
- 黄色の丸が「子うさぎ(1つがい)」、
- 青の丸が「親うさぎ(1つがい)」 を表しています。
このような図では、一番上の頂点を「根(ルート)」と呼びます。
不思議なことに、数学では木の図を上下逆さに描くのが一般的で、枝は上から下に向かって広がっていきます。つまり各頂点から枝が下向きに出ています。
この木の構造にはいくつかの特徴があります:
- 各頂点(丸)から出ている枝の数は1本か2本
- 最も下にあって枝が出ていない頂点を「葉」と呼びます
- 根を「レベル0」とし、下に進むにつれて「レベル1」「レベル2」…とレベルを段階的に番号付けします
図2の右側に書かれている数字は、そのレベルに存在する頂点(丸)の数を表しています。また、括弧の中の数字は青丸(親うさぎのつがい)の個数を示しています。
ここで、レベル n にある頂点の個数を uₙ と表すことにしましょう。
このとき、数列 u₀, u₁, u₂, … は、先ほど説明したフィボナッチ数列になっています。さらに興味深いのは、括弧内の青丸の数(親のうさぎの数)もまたフィボナッチ数列になっているという点です。
フィボナッチ数列の漸化式
もう一度、図2を見ながらフィボナッチの木を復習してみましょう。
レベル n における uₙ は「n ヶ月後のつがいの総数」、その中の uₙ₋₁ は「親うさぎのつがい数」を表しています。したがって、その月に新しく生まれた子うさぎのつがい数はuₙ − uₙ₋₁ となります。
子を産むのは親うさぎ(uₙ₋₁)だけですから、次の月 (n + 1 ヶ月後) の総つがい数は
親からの新生児(uₙ₋₁)を加えて:
uₙ₊₁ = uₙ + uₙ₋₁
という関係式になります。
つまり「前の2項の和が次の項になる」というフィボナッチ数列の規則を満たしています。
フィボナッチ数列の定義と拡張
もともとフィボナッチが定義していた数列は:
1, 2, 3, 5, 8, …
という形式でしたが、のちに前に 1 を加えて:
1, 1, 2, 3, 5, 8, …
という形が広まりました。さらに近年では、最初に 0 を加えて:
0, 1, 1, 2, 3, 5, …
という形式が使われることもあります。
このように、フィボナッチ数列は次のような漸化式(再帰的な定義)で表されます:
u₁ = 1, u₂ = 1, uₙ₊₁ = uₙ + uₙ₋₁ (n = 2, 3, 4, …)
自然界とフィボナッチ数列
フィボナッチ数列は、数学の問題だけでなく、自然界のあちこちにも登場します。その理由の一つとされているのが、「自己相似性」です。これは、成長していく過程で、それまでに作られた形と似た構造を繰り返すこと。このようにして情報やエネルギーを効率よく使い、規則的で美しいパターンが自然に生まれていると考えられています。
黄金比とフィボナッチ数列
フィボナッチ数列には、もうひとつ興味深い性質があります。それは、隣り合う2つの項の比 ―― つまり、uₙ₊₁ ÷ uₙ ―― が、ある特別な数に近づいていくというものです。
その特別な数とは、黄金比(おうごんひ)です。
たとえば、次のように数列の比をとってみると:
- 2 ÷ 1 = 2.0
- 3 ÷ 2 = 1.5
- 5 ÷ 3 ≈ 1.666…
- 8 ÷ 5 = 1.6
- 13 ÷ 8 ≈ 1.625
- …
このように、n が大きくなるにつれて、比はだんだん黄金比 φ ≒ 1.618… に近づいていきます。
黄金比は、人間が最も美しいと感じる比率ともいわれ、ピラミッドやパルテノン神殿、ルネサンス期の絵画や現代のロゴデザインなど、建築や芸術、商業デザインの中にも数多く用いられています。
フィボナッチ数列と黄金比の関係は、数学の歴史の中でもたびたび注目されてきました。黄金比のより詳しい内容については、別の記事で改めてご紹介したいと思います。
関連記事以下の記事で詳しく解説しています++。
まとめ
フィボナッチ数列は、単なる数学の問題にとどまらず、自然や芸術、デザインの中にも繰り返し現れる、奥深い数列です。その背景には「自己相似性」や「成長の最適化」といった自然のしくみが関係しているとも言われています。
そして、隣り合う項の比が黄金比に近づいていくという性質は、数列の美しさと神秘性をより一層引き立てています。
日常の中にも、こうした「数の不思議」がひっそりと隠れているかもしれません。身の回りにある自然やデザインの中に、フィボナッチ数列や黄金比のようなリズムを見つけてみるのも楽しいかもしれません。



