1-4.公理と量

原論の幾何学第1巻〜第4巻の大きな特徴は、角度、長さ、面積、体積などを数値として扱っていないことです。これらは量として扱います。原論の第７巻になってやっと自然数がでてきます。比が最初に現われるのは第5巻、相似が現われるのは第6巻、数が現われるのはやっと第7巻になってからです。第1～4巻の幾何学はこれらの概念を使わずに展開されています。

数学とは元来、数を対象とした学問として発達してきました。現代数学では数以外のものも扱うようになってきましたし、実数以外にもいろいろな数を扱うようになってきました。これらの扱いは、原論の量の扱いにとてもよく似ています。ギリシアの数学を正しく知るためにも、また数学における数の発展を知る上においても、原論の量の扱いを知ることはとても有用だと思います。

ユークリッド『原論』に出てくる9つの公理

「ギリシアの幾何学は対象が図形なので直観的に分かりやすい」、「現代数学と違って公式が出てこない」などといいながら、ここで長々と公理について述べなければなりません。しかし、内容はみなさんがよくご存じの数についてですから、難しくはありません。最初はサーッと目を通すだけで、必要になったら後で読み返してもらっても結構です。

ユークリッド『原論』：9つの公理

• 公理 1等しいものに等しいものはまた互いに等しい。
• 公理 2等しいものに等しいものが加えられれば、全体は等しい。
• 公理 3等しいものから等しいものが引かれれば、残りは等しい。
• 公理* 4不等なものに等しいものが加えられれば、全体は不等である。
• 公理* 5等しいものの2倍は互いに等しい。
• 公理* 6等しいものの半分は互いに等しい。
• 公理 7互いに重なり合うものは互いに等しい。
• 公理 8全体は部分より大きい。
• 公理* 92直線は面積を囲まない。

(※アスタリスク (*) の付いた公理*4 公理*5公理*6公理*9は後世の挿入だと考えられています。)

『等しい』という概念について

数学では“等しい”という概念がとても重要な働きをします。上の公理で、“等しい”とは“同じ量”という意味で用います。公理 7 の「ぴったり重なり合う」ことを以下では合同と呼ぶことにします。すると、公理 7は「合同なら等しい」となります。したがって、“等しい”という概念は“合同”より広い意味となります。例えば三角形と四角形は合同ではありませんが、同じ面積であれば“等しい”といいます。

『原論』では量が数値として表されることはありません。それどころか、長さ、面積、体積という言葉さえありません。2つの線分が等しい、平面図形が等しい、立体が等しいとは、それぞれ長さが等しい、面積等しい、体積が等しいことを意味します。つまり、“長さ”というのは線分の属性なのですが、まだ“線分”という親から自立して一人歩きできるようになっていなかったのです。以下では、たとえば「三角形 ABC の面積は三角形 DEF の面積と等しい」ことを式で

△ABC ＝ △DEF

と書きます。この式は上の文章の単なる略記法だと思ってください。また、略記法 △ABC は「三角形 ABC」自身を表すときと、「三角形 ABCの面積」を表すときとがあります。

量には大小関係が定まるときがあります。たとえば図K1-4-1のように、△DEF が △ABC に含まれるとき、△DEF は △ABC より小さい、あるいは △ABC は △DEF より大きいといい

△DEF ＜ △ABC, △ABC ＞ △DEF

と書きます。

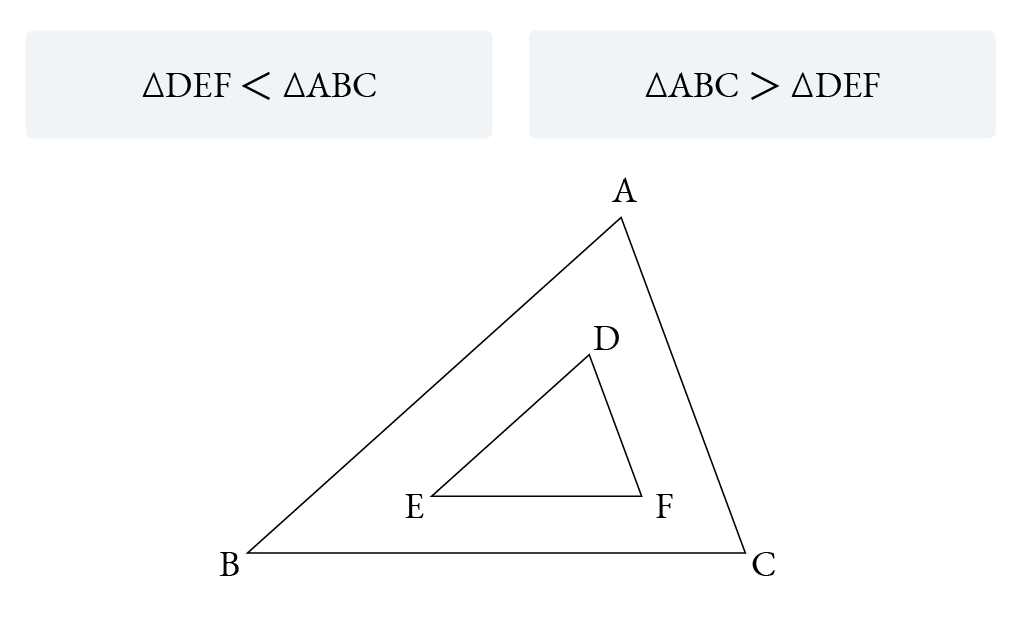
等しいという関係や大小関係は同じ種類の量に対してしか定義されません。例えば、長さと面積は比較することができません。

9つの公理と表記法

上の公理には、加えるとか引かれるという言葉が出てきます。量の間には足し算と引き算が定義されています。ただし、同じ種類の量に限ります。例えば、長さと面積は種類が違うので足したり、引いたりできません。足し算を ＋、引き算を –、等しいことを ＝ で表し、現代数学の式で表すと、公理1、公理2、公理3 は次のように表されます。ここで、A, B, C は同じ種類の量です。

• 公理1A＝B, B＝C ⇒ A＝C
• 公理2A＝B ⇒ A＋C ＝ B＋C
• 公理3A＝B ⇒ A – C ＝ B – C

公理1は「AがB に等しく、かつ B が C に等しいなら A は C に等しい」と読みます。すなわち、コンマ (,) は“かつ”と読み、記号 ⇒ は“ならば”と読みます。公理2は「A と B が等しいなら、 A＋C は B＋C に等しい」と読みます。公理3も同様です。

公理1は現代数学における同値の公理と呼ばれるものの一部で、同値の公理は、これ以外に次の2つが必要です。

• 公理aどんなものも自分自身に等しい。すなわち、任意の A に対し A＝A である。
• 公理bもし A が B に等しいなら、B は A に等しい。すなわち A＝B なら B＝A である。

みなさんの中には、どうしてこんな当たり前のことをわざわざ言う必要があるのだ、と疑問に思う人がいることでしょう。公理aと公理bについては、現代数学で“等しい”とか“大小関係”以外にもいろいろな“関係”があることを学んでこれらの公理の有用性を認識するまでは、覚える必要はないと思います。古代ギリシア人がこれらを思いつかなくて当然です。むしろギリシア人が公理1 ～公理* 9 を設定したことこそ驚くべきことです。以下の議論で、これらの公理がどのように使われているかを観察してください。

公理* 9は少し分かりにくいのですが、「もし2点を結ぶ直線が2本あったらその間に面積ができてしまうが、そういったことはない」という意味のようです。したがって次のように言い換えておきます。

公理* 9与えられた2点を通る直線はただ一つ存在する。

まとめ

原論の幾何学の大きな特徴のひとつに、数値が現れないことが挙げられます。角度、長さ、面積、体積は“数”ではなく“量”として扱われています。また、この公理にでてくる「等しい」という概念は、数学ではとても重要です。次回はいよいよ幾何学の基本的な概念である『線分』と『角度』についてみていきます。