ガリレオが用いた「比の理論」

 

古代のギリシア数学

比に関する基本規則

ガリレオの業績の偉大さを理解するには、当時の数学がどんなものであったかを知る必要があります。数学は、古代から現在の数学があったわけではなく、大勢の人によって作られてきたのです。ここではガリレオが用いた古代ギリシアの「比の理論」を復習しておきましょう。

古代ギリシアでは、“数”とは自然数だけで、長さ、面積、体積、角度はそれぞれ違った種類の“量”として扱われました。数に関しては四則演算が許されますが、量に関しては許されるのは足し算と引き算だけで、それも同じ種類のものに制限されていました。たとえば、長さと面積は種類が違うので足せません。足し算が許されるのですから、“自然数倍”は許されます。たとえば量 a の3倍は、aを3個足した a＋a＋a 実現できます。この制限された体系で、ユークリッドの『原論』は高度な比の理論を作り上げました。

□(a, b) で底辺が a 高さが b の長方形を表し、□²(a) で一辺が a の正方形（英語では square(平方)）を表します。つまり □²(a) は、数値の a² ではなく、言葉で「a の平方」と書かれているものとみなしてください。□(a, b) は長方形を表す時と長方形の面積を表すときとがあります。

次は比に関する基本規則で、比の定義から得られるのですが証明は省略します。a, b, c, x, y は線分（の長さ）です。

a : b ＝ x : y  ⇒ b : a ＝ y : x                   転置
a : b ＝ x : y  ⇒ a : x ＝ b : y                   内項の交換
a : c ＝ x : c  ⇒ a ＝ x                          右項の一致
a : b ＝ □(x,a) : □(x,b)                          同一底辺

相似の概念

比の理論で中心的議論を果たすのが 相似 の概念です。ここで用いる記号を説明しましょう。

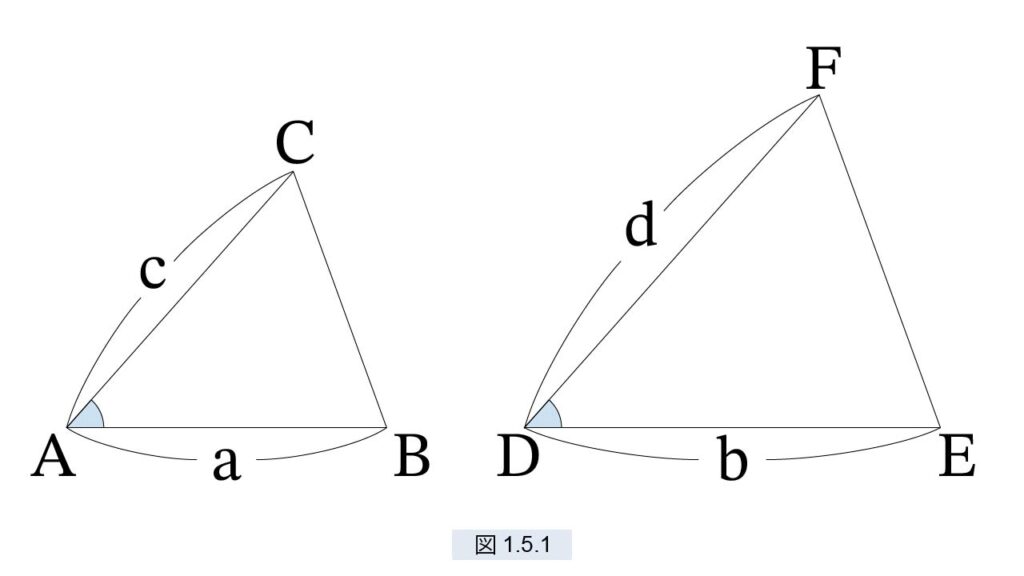
三角形 ABC と三角形 DEC が相似である必要十分条件は
∠A＝∠D, a : b ＝ c : d が成立すること

これを記号で表すと次のようになります。

△ABC ∝ △DEF ⇔ ∠A＝∠D, a : b ＝ c : d

もちろん古代ではこのような記号は用いませんが、本連載の目的は古代の数学を一般の人に知ってもらうためなので、記号と式を使います。しかし、これらの記号の使用は上のように直接言葉に変換できるものに限っています。

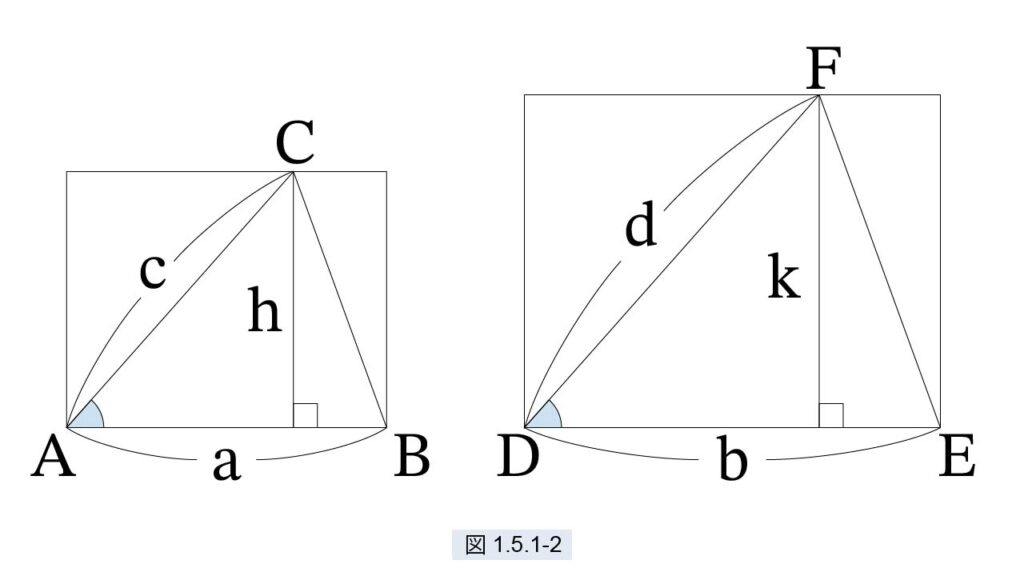
図1.5.1-2 の2つの三角形を考えます。C から AB に下ろした垂線を h、F からDE に下ろした垂線を k とします。このとき次が成立します。

△ABC : △DEF ＝ □(a, h) : □(b, k)
＝ □²(a) : □²(b)                                        (1)

(1) の証明はこの節の終わりに述べます。

グノモンの定理

長方形の面積

ガリレオは、自然数以外の数 a と b に関しては、掛け算 a×b を考えることができませんでした。その代わりに長方形 □(a, b) の面積を考えたのです。面積や長さは量なのです。

□(a, c) と □(b, d) の2つの長方形を考えます。図1.5.2 のように2つの長方形を重ねてできる L形の図形をグノモンといいます。

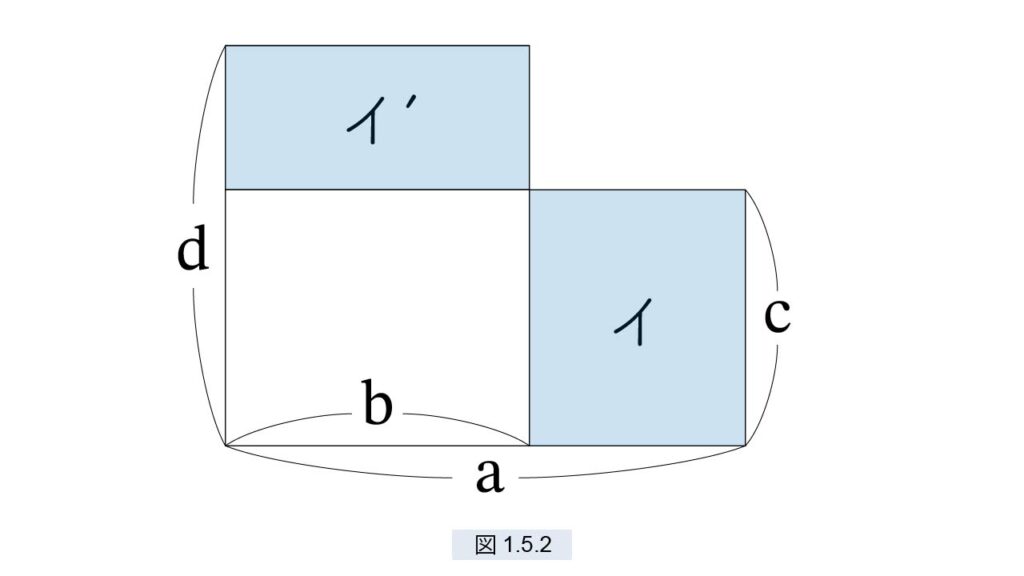
重複した部分を内部長方形、それ以外の部分を突起部といい、2つの辺を延長してできる長方形を外部長方形と呼ぶことにします。図で (イ) と (イ’) が突起部です。次は明らかです。

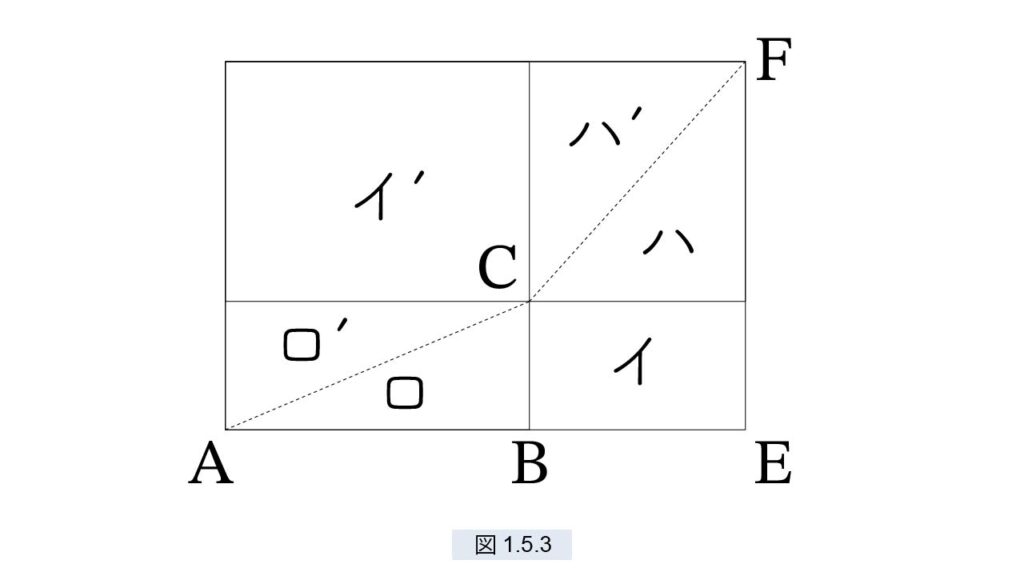
〔グノモンの定理 〕の証明

CA と FC は小長方形の対角線だから、

(ロ)＝(ロ’)、(ハ)＝(ハ’)

よって

(イ) ＝ (イ‘)
⇔  (イ)＋(ロ)＋(ハ) ＝ (イ’)＋(ロ’)＋(ハ’)
⇔  FCA は外部長方形の対角線。

〔外項内項の積〕の証明

□(a, d) と □(b, c) を図1.5.4のように置き、グノモンを作ります。外部長方形を描き、図のように記号を振ります。

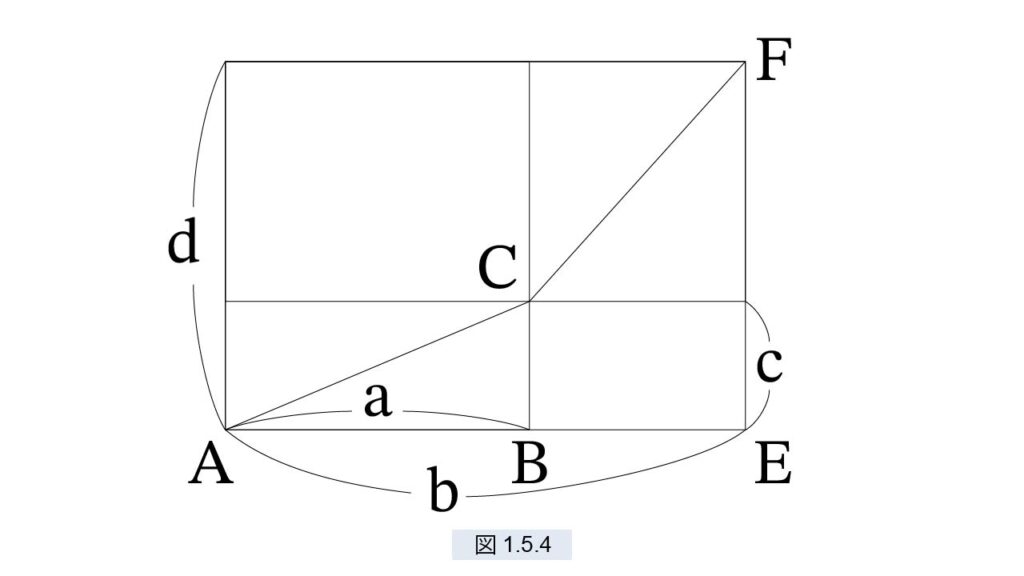
すると グノモンの定理 より、次が成立します。

□(a, d) ＝ □(b, c)  ⇔ C は対角線FA上
⇔ △CAB ∝ △FAE
⇔ a : b ＝ c : d

面積の和の計算

作図〔a : e ＝ x : b〕

量には和が定義されると述べましたが、例えば面積の和は実際にはどのように計算されるのでしょうか。三角形は同じ面積の長方形に直せますから、長方形が足せればよいことになります。2つの長方形を足すには、次の作図により、底辺を揃えることで足せます。

長方形 □(a, b) と辺 e が与えられたとします。このとき □(a, b) ＝ □(e, x) を満たす長方形 □(e, x) を作図します（図1.5.5）。

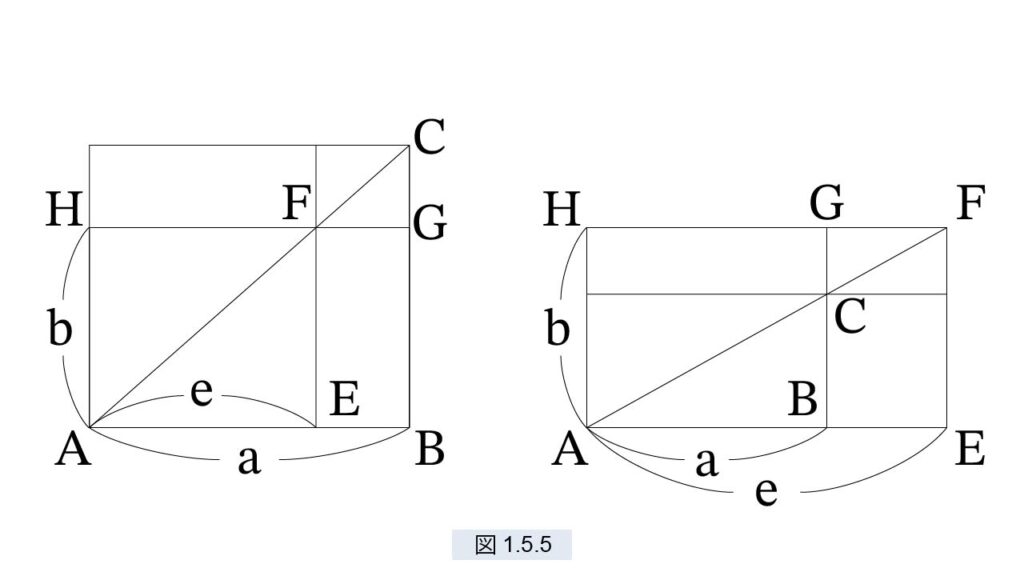
□(a, b) をABGH とします。e ＜ a のときは AB 上に、e ＞ a のときは AB の延長線上に点 E を AE＝e となるように取ります。E を通る AB の垂線を引き、HG または HG の延長線との交点を F とします。AF またはその延長線と、BG またはその延長線との交点を C とすると、BC が求める x です。 2つの長方形を足すには、底辺を揃えることです。底辺が同じ長方形は、積み上げることによって長方形となるからです。上の作図法を使えば任意の長方形の底辺を e に揃えることができます。

同次元の制約

ガリレオの時代、ヨーロッパの代数では〔同次元の制約〕という規則が守られていました。線分は 1次元、面積は2次元、体積は3次元と見て、次元の異なるもの同士の足し算はできないという規則です。上で述べた「違った量の足し算ができない」という規則を言い換えたものです。ガリレオはこの規則を破っています。後の節で見るように「面積を距離（長さ）」とみなしているからです。これは、任意の長方形は、単位 e を底辺とする長方形に変換でき、上で述べた〔同一底辺〕の規則により、面積の比は長さの比に変換できるからです。

□(e, a) : □(e, b) ＝ a : b

比の掛け算

比には掛け算（積）が定義されています。現在の皆さんは、比 a : b は分数 a/b とみなしているので、次を比の積の定義だと理解していただけると思います。

(a : b)×(c : d) ⇔ □(a, c) ＝ □(b, d)　　　( 2 )

特に (a : b)×(a : b) を (a : b)² と書き、(a : b) の平方といいます。

ユークリッドの『原論』では、比の積を定義して、(2) を定理として証明しています（2つの長方形 □(a,c) と □(b,d) の面積の比は、辺の比 a:b と c:d の積となる）。ここでは (2) を比 a:b と c:d の積の定義とします。比 a:b を分数 a/b とみなし、(2) を現代式に表わすと次のようになります。

\( \frac{a}{b} × \frac{c}{d} = \frac{a×c}{b×d} \)　　　(2′)

式 (2’) は、分数 a/c と b/d の積の定義と読むことができます。

比例中項の作図

比 (a : c) ＝ (d : b) で中項 c と d が等しいとき、c＝d を a と b の 比例中項といいます。比 (a : c) ＝ (c : b) は、〔外項内項の積〕の定理を使って □(a, b) ＝ □²(c) と書けます。したがって、現在の数学では c = √ab と書けます。

作図〔比例中項〕  a : x ＝ x : b

2つの線分 a と b が与えられたとき、a と b の比例中項 x は次のように作図できます（図1.5.6）

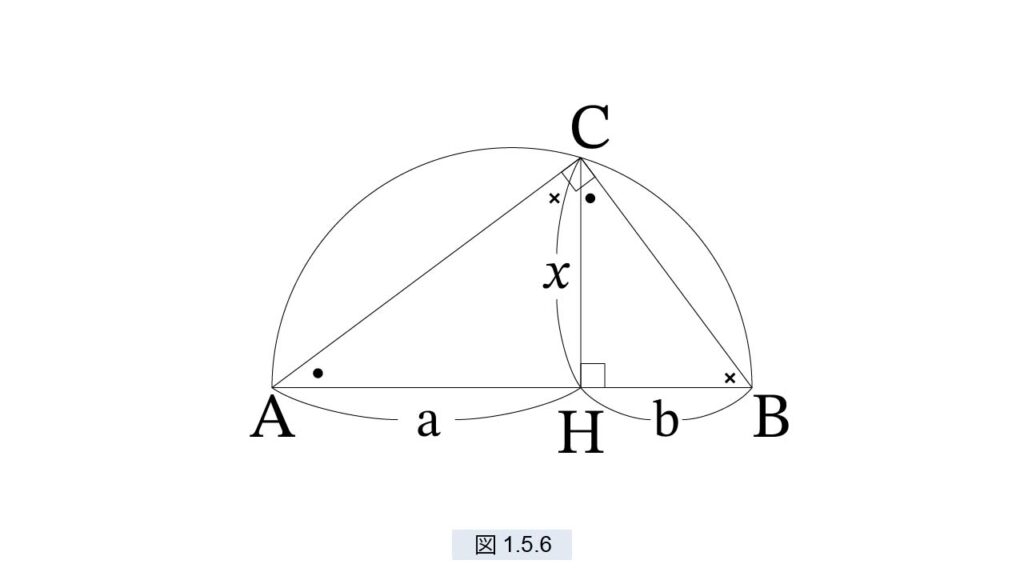
長さ a＋b の線分 AB を描きます。AH＝a, HB＝b とします。直径 AB の半円を描き、H における AB の垂線と半円との交点を C とします。すると ACB 直角三角形で、△ACH と △CHB は相似だから、a : x ＝ x : b が成立します。

c を a と b の比例中項とすると、c² ＝ ab ですから次が成立します。

a : b ＝ a² : ab ＝ a² : c²
＝ ab : b² ＝ c² : b²

上の2行目は、a : b の左項と右項に b を掛け
a : b ＝ a×b : b×b
となることから得られます。

(1)の証明

a:b＝h:k  ∴ a:h ＝ b:k
a:h ＝ □(a,a) : □(a, h), b:k ＝ □(b,b) : □(b, k)

よって、

□(a,a) : □(a, h) ＝ □(b,b) : □(b, k)

内項の交換より

□²(a) : □²(b) ＝ □(a, h) : □(b, k)