オイラーの多面体定理 とは

オイラーの多面体定理とは？──形の不思議にひそむ美しい公式

18世紀の偉大な数学者レオンハルト・オイラーは、ある重要な関係式を多面体の構造から発見しました。それが有名な：

「 頂点の数 ー 辺の数 ＋ 面の数 ＝ 2」

という式です。

この関係は、「オイラーの多面体定理」と呼ばれ、特に凸多面体（角や辺がとがっていない閉じた立体）において常に成り立ちます。

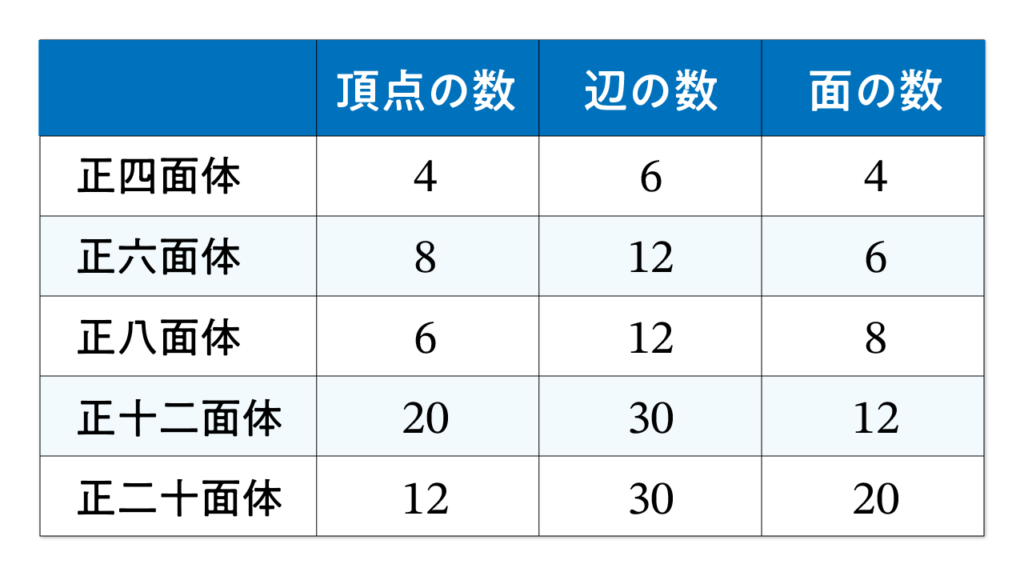
たとえば、正四面体（頂点4、辺6、面4）の場合：

4 – 6 + 4 = 2

この不思議な等式は、どんなに形が違っても「凸多面体」であれば常に 2 に等しくなるという、幾何学における基本かつ美しい法則のひとつです。

オイラーの定理は、のちに位相幾何学（トポロジー)の発展にも大きく影響を与え、形の“本質的なつながり方”を研究する土台となりました。

正多面体とは？──対称性が生む究極の立体美

多面体とは、多くの面によって囲まれた立体のことを指します。その中でも、特に高い対称性を持つのが正多面体です。

正多面体とは、次の2つの条件を満たす多面体のことです：

(1) 各面がすべて同じ正多角形である
(2) 各頂点において出会う正多角形の個数が等しい

この2つの条件を満たす立体は、驚くことにたった5種類しか存在しません。

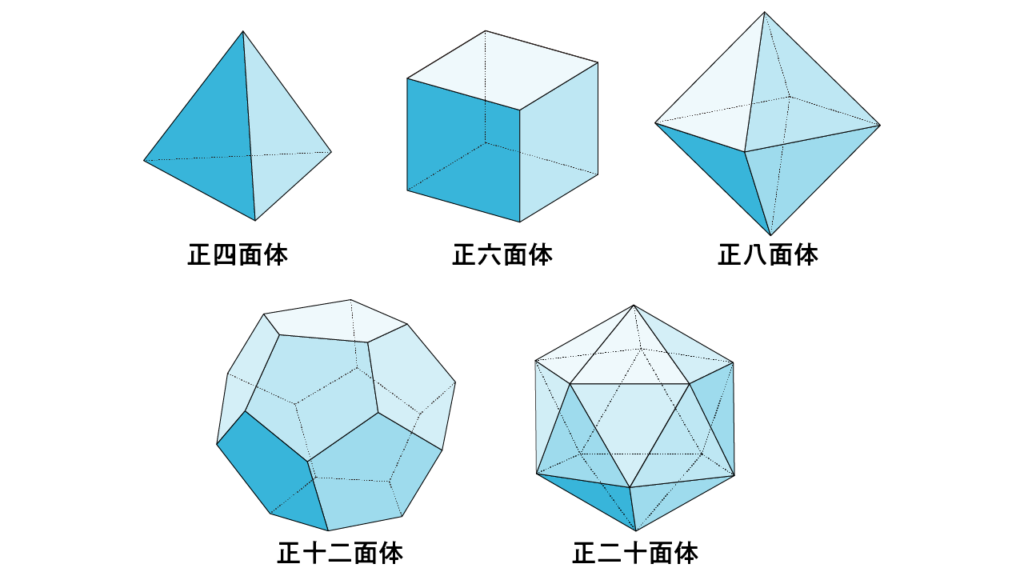
プラトン立体──哲学と幾何が交差した形

この5種類の正多面体は、古代ギリシアの哲学者プラトンにちなんで「プラトン立体」とも呼ばれます。

プラトンは、世界を構成する基本的な4つの元素（火・空気・水・土）に、それぞれ正多面体を対応させました。残る1つの立体には、宇宙そのもの（エーテル）という象徴的な意味が込められていたとされています。

正多面体にはいくつもの不思議な性質があります。古代から現代にいたるまで、正多面体は数学者の興味の対象となってきました。

正多面体はプラトン立体ともよばれ、世の中に5種類しか存在しません。古代ギリシアの人々は、宇宙を構成する元素が、火、空気、水、土の4つであると考えていました。プラトンはこの4つの元素に5つの正多面体のうちの4つを割り当てました。

正多面体はなぜ5つしかない？

数学的に証明されている通り、正多面体は空間内において5種類しか存在しないことがわかっています。

この事実は、角度の和や立体の構成条件を満たす正多角形の組み合わせが限られているためです。

これらの立体は、古代から現代にかけて美・対称性・数学的完全性の象徴として、数学者・哲学者・芸術家たちの関心を集め続けています。

プラトン立体についてはこちらの記事で詳しく解説しています ▼
史上最も有名な立体「プラトンの立体」

まとめ

オイラーの多面体定理は、一見ばらばらに見える立体にも、数の世界の秩序が通じていることを示しています。

この定理は単なる図形の公式ではなく、立体の構造に潜む本質的な関係性を捉える手がかりとなり、やがてトポロジー（位相幾何学）という現代数学の分野へと発展していきました。

「かたちを数で読む」という視点が、どれほど深い洞察を与えてくれるか――

オイラーの定理はその力強い証明であり、今もなお多くの人の知的好奇心を刺激し続けています。