円周率 とは

円周率とは

円周率とは、「円周を直径で割った値」のことで、円周の長さが直径の何倍かを表す値です。これはどんな大きさの円でも変わらず、常に同じ比率になります。

この値は、ギリシア文字の π（パイ）で表され、

π ≒ 3.14159265358979…

と、無限に続く小数です（循環しません）。

円周率は数学や科学、工学のあらゆる分野で使われており、最も有名な定数の一つです。

無限につづく数

円周率 π の小数部分は、

π ≒ 3.14159265358979…

と、どこまでも終わらずに続く数です。これは「1億桁」「100億桁」といったレベルではなく、本当に“無限”に続くという意味です。

しかも、円周率はただの長い数ではありません。

π は、どんな整数 a と b を使っても「a ÷ b」という形の分数で正確に表すことができない数です。

このような数を「無理数（むりすう）」といいます。

一方で、2 や 1/3、0.25 のように、分数で表せる数は「有理数（ゆうりすう）」と呼ばれます。

つまり、π は「無限に続く小数」であり、「分数にもできない特別な数」なのです。

アルキメデスが考えた円周率

円の直径と円周の比率は、古代バビロニアの時代から使われていました。

しかし、これを数学的な方法で厳密に求めようとした最初の人物の一人が、古代ギリシアの数学者アルキメデスです。

アルキメデスは数学だけでなく、物理、工学、天文学など多方面で活躍した天才で、球の表面積や体積や放物線の面積の計算など、数学史に残る多くの成果を残しました。その中でも、円周率 π に関する研究はとりわけ有名です。

彼は、半径1の円に内接する正多角形と外接する正多角さを用いて、円周率を近似する方法を考案しました。

まずは正6角形から始め、その外接多角形の周長が円周よりも大きいことを確認します。そこから、正12角形、正24角形、正48角形、正96角形…と順に辺の数を倍増させていきます。

このようにして計算された正多角形の周長は、円周の長さにどんどん近づいていきます。ただし、外接多角形の周長は常に円周を上回るため、円周率の上限を与える数として扱われます。

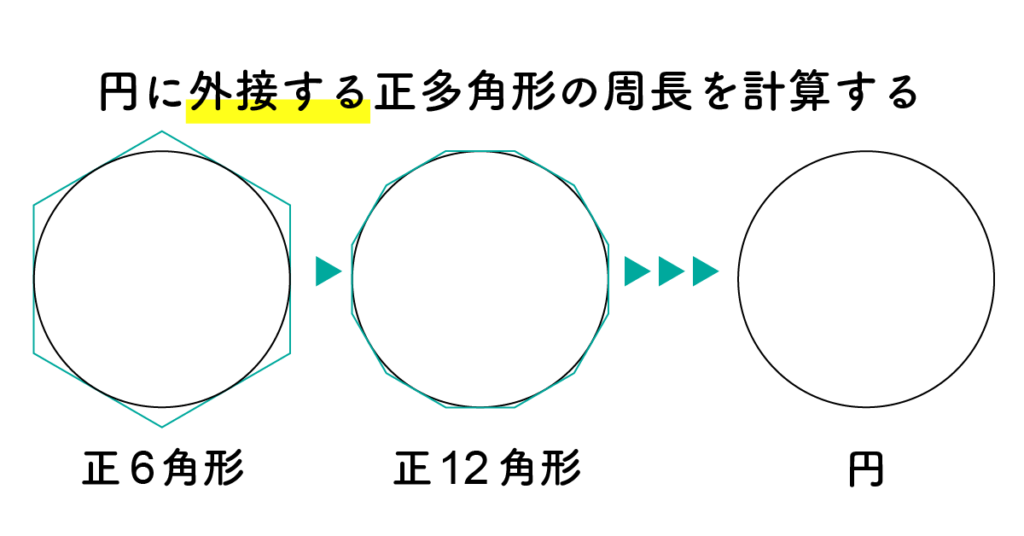
同時に、内接多角形を使えば円周の下限も得られるため、アルキメデスはこの二つの間にπがあることを示しました。正6角形から始め、正12角形、正24角形、正48角形と頂点の数を増やして計算していき、正96角形まで計算することで、 22/7 という極めて高精度な近似値を導き出しました。

これは紀元前3世紀の成果としては驚異的であり、円周率の歴史における大きな前進でした。

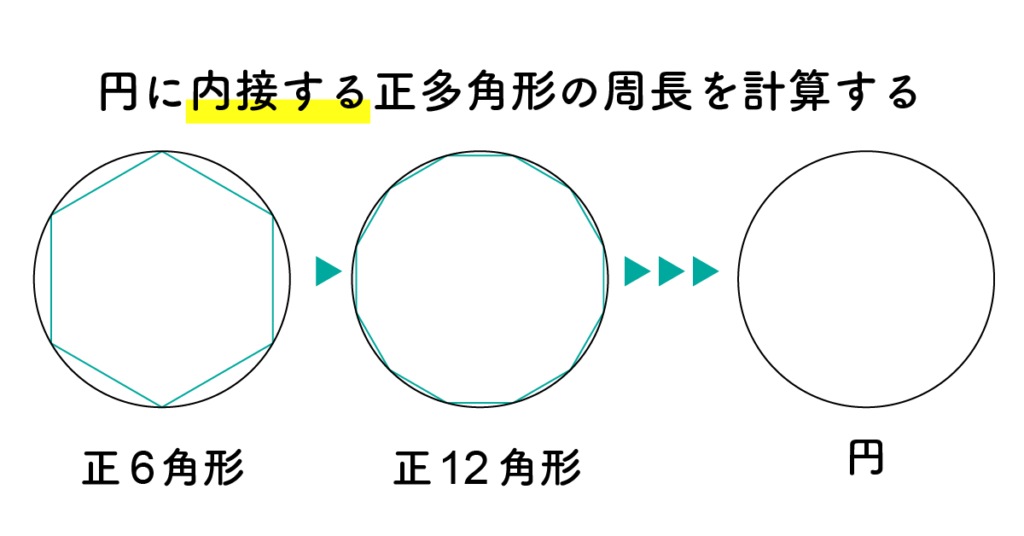
アルキメデスは円周率πを、直径1 の円に内接する正多角形と外接する正多角形の周長を計算することで求めました。

Web連載 アルキメデスの求積 2-3 πの源流

ピラミッドの謎とπ

古代エジプトのピラミッドには、長いあいだ人々を魅了してきた数々の謎があります。その中のひとつが、円周率 π に関する謎です。

なんと、ピラミッドの寸法の中に円周率 π が現れるという説があるのです。

たとえば、クフ王の大ピラミッドを例に取ると、底辺の長さと高さをもとに計算したとき、

「高さ × 2π ≒ 底辺の周の長さ」

という関係が成り立つように見えるのです。

このことから一部の研究者は、古代エジプト人がすでに円周率を知っていたのではないか、あるいは意図的にその値を設計に取り入れたのではないかと考えました。
古代エジプト人は円周率をすでに発見していたのでしょうか。

ピラミッドに隠された数の謎は、今なお人類の知的探究心を刺激し続けているのです。

ピラミッドの数に関する3つの謎『円周率の謎』『黄金比の謎』『地球の緯度の謎』を解明するWeb連載

まとめ

円周率 π は、単なる「3.14」ではありません。

その小数はどこまでも終わらずに続き、分数でも正確に表せない無理数として、今なお人類の知的挑戦を促しています。

古代ギリシアのアルキメデスが多角形で近似し、現代のコンピュータが何兆桁も計算しているこの数は、時代も文明も超えて、数学という言語で私たちをつなげていると言えるでしょう。

円周率の探究は、単なる数字の話ではなく、「世界をどう見るか」という哲学的な問いにもつながっています。

あなたも、πに秘められた奥深い世界に、少しだけ足を踏み入れてみませんか？