
8.等加速度運動の再検討|ガリレオの法則は正しかったのか?
ページ目次
数学の移り変わり
ガリレオ以降の数学
ガリレオは、「速度は距離に比例するのではなく、時間に比例する」という事実に気がつくと「落下の理論」が急速に進みました。これは「落下の理論」だけにとどまらず、数学や物理学全般に影響を及ぼすことになるのです。
ガリレオが用いた数学的言語は幾何学であり、特に比の理論でした。しかし、『原論』の幾何学は、数値を扱わないという大きな制約を持っていました。当時は大航海時代の真っただ中で、海外から多くの知識が入ってきて、実践的な科学の重要性が認識されていました。航海術には、日時や緯度経度を知るために天文学、地理学、三角法などの知識が必要です。多くの人が「数学の必要性」を唱えていましたが、具体的にどのように適用していいのやら分かりませんでした。
それまでの幾何学では、個数を表す自然数以外、長さや面積は数値を伴わない“量”でした。ガリレオは“時間”とか“速度”を線分で表しただけでなく、それらを数として扱い、実測し、計算し、理論を打ち立てました。
実数という概念の登場
ガリレオ以降数学史を語るのに、“実数”という概念を使っていいように思います。長さや重さ、時間や速度など、もろもろのものはすべて実数だと考えるようになってきたのです。だれも「実数とは何か」などという疑問は持ちません。実数とはもともと自然界に実存するものだと考えたのです。
実数という概念が真剣に議論されるようになったのは、やっと19世紀に入ってからです。こういった、伝統を無視した型破りで無頓着な使用が数学を飛躍的に進展させたのです。 具体的にいうと、面積 □(a. b) は積 a×b とみなされ、比 a : b は分数 a/b とみなされるようになったのです。長方形の面積はもともと「底辺と高さの積」で計算されていましたから、「実数 a と b の積を、底辺a と高さ b の面積として定義する」というのは自然な事でした。では比と分数に関してはどうだったのでしょうか。ガリレオの「落下の理論」がその後どのように扱われるようになったか見ていきましょう。
数式の扱いについて
以下で述べることは、ガリレオの数学がその後どのように変貌するかを述べたものです。式の変形がたくさん出てきます。こうした式の扱いに慣れていない方は、無理に理解しようとせずざっと読み通してください。このことは代数一般に言えることですが、以下で出てくる式とほとんど同じ式がガリレオ以降の数学で頻繁に現れますから、公式として無理に覚える必要はありません。式の運用についても同様です。外国語の学習では、新しい単語を習得するにはその単語に20回出会う必要がある、という意見を聞きます。式の変形も同じで、何度も同じ変形を見るうちに自然と体得するものです。
等加速度運動
時間平方則
等加速度運動とは、速度が時間に比例する運動のことですから、時刻 t1, t2、速度 v1, v2 に対し次が成立します。
\( v_1 : v_2 = t_1 : t_2\)
〔内項の交換〕を実行すると、
\( v_1 : t_1 = v_2 : t_2\)
となります。『原論』の比の定義によると、比が定義できるのは同種の量に限ります。同種というのは「どちらが大きいかが比較できるもの」で、“速度”と“時間”はとでは、大きさが比較できないので同種ではありません。したがって、厳密な比の定義によると「速度 : 時間」という比は許されないはずですが、ガリレオは時間も速度も線分にしてしまいました。線分どうしは同種なので、内項の交換が許されます。
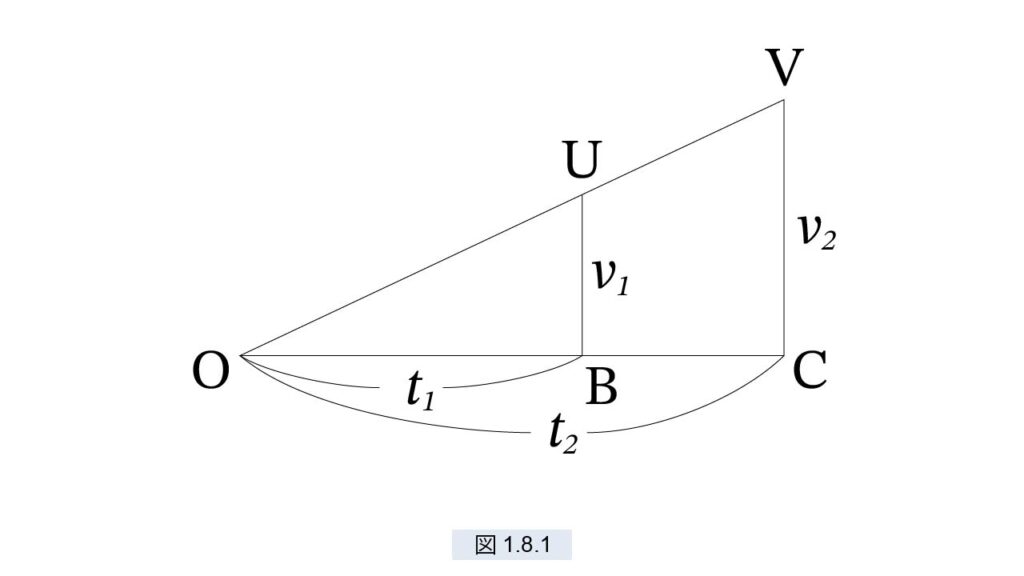
図1.8.1 を見てください。△UBO と △VCO は幾何学でよく現れる相似な三角形で、古代ではピラミッドや山などの高さの計測に用いられました。そこでは
\( \frac{v_1}{t_1} = \frac{v_2}{t_2} = a \)
という式が用いられました。ここで a は直線 OV の傾きの度合いを表す定数で、比例定数といいます。ガリレオ自身は比例定数を用いることはありませんでしたが、ガリレオの著作を読んだ学者たちはすぐにこれに気がつきました。時を経ずして、速度を表す直線は
\(v = at\) (1)
と表されるようになります。また時間 t で移動する距離 s は、三角形の面積ですから
\( s= \frac{1}{2} at^2 \)
となります。これはガリレオの〔時間平方則〕に他なりません。つまり、等加速度運動とは (1) で示される速度変化のことであり、その移動距離は (2) で表されるとしたのです。
これだけではまだ足りません。〔ガリレオの公準〕は、これからは出てこないのです。
ガリレオの公準 は成立するか
前節で述べた 図1.7.3 をもう一度考えましょう。( 図1.8.2 として以下に再掲)
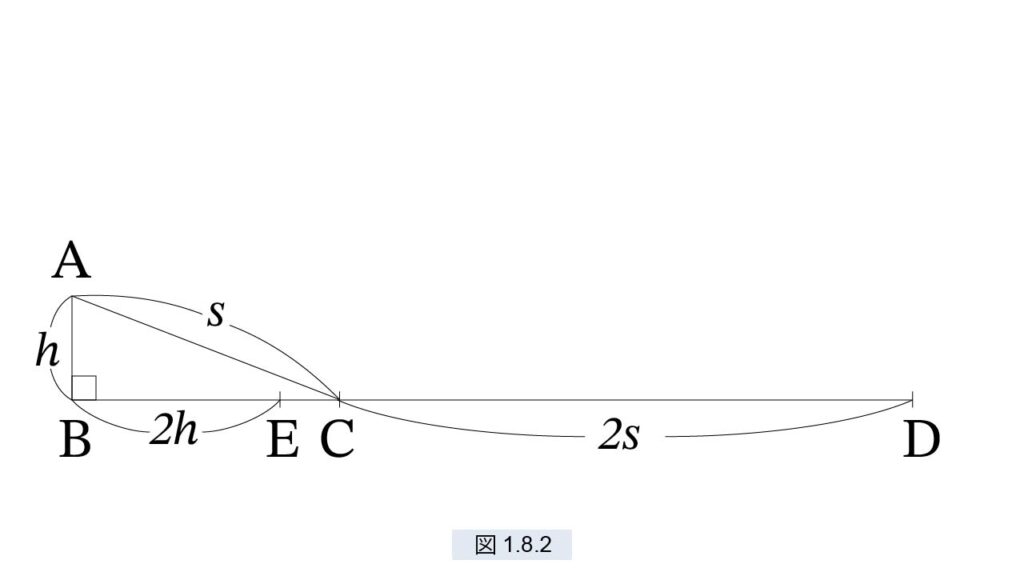
\( AB=h, AC=s, time(AB)=t_1, time(AC)=t_2\)
とします。鉛直落下 AB の速度が次の (3)で、坂 AC の速度 (4) で定まるとします。
\( v = gt \) (3)
\( v = at \) (4)
ここで比例定数 a と g の関係を調べます。g は将来重力加速度と呼ばれることになる定数ですが、ここでは単なる定数だと思ってください。〔ガリレオの公準〕が成り立つとすると、B点と C点での速度が等しいことから
\( gt_1 = at_2 \hspace{20pt} \therefore \frac{a}{g} = \frac{t_1}{t_2} \)
が成り立ちます。すると前節の定理1 より
\( \frac{t_1}{t_2} = \frac{h}{s} \)
ですから、
\( \frac{a}{g} = \frac{h}{s} \) すなわち \( a : g = h : s \) (5)
となります。
〔ガリレオの公準〕を仮定すると、a と g が (5) の関係にあることが分かりました。以下では (5) が〔ガリレオの公準〕の代わりになることを示します。つまり (3), (4), (5) だけの仮定のもとでガリレオの公準が成り立つことがいえます。
図1.8.2 における A からの落下を考えます。点 B での時間 t1 と C での時間 t2 は、面積の公式 (2) で計算できます。
\( h = \frac{1}{2}gt_1^2 \hspace{20pt} s = \frac{1}{2}at_2^2 \)
これを使うと、B における速度 v1 = gt1 と、c における速度 v2 = at2 は次のように計算できます。
\( v_1^2 = (gt_1)^2 = g \times gt_1^2 = 2gh \)
\( v_2^2 = (at_2)^2 = a \times at_2^2 = 2as \)
ここで (5) の a = hg/s を最後の式に代入すると
\( v_2^2 = 2as = 2s \times \frac{hg}{s} = 2hg \)
となり、v1 = v2 が成立します。したがって〔ガリレオの公準〕が成立します。
倍距離則 は成立するか
〔倍距離則〕も成立することを示しましょう。落下 AC に要した時間はt2 で、C での速度は v2 = at2 であり、速度 v2 で t2 時間の等速度運動で移動する距離は v2t2 です。したがって
\( v_2t_2 = at_2^2 = 2s \)
となり、〔倍距離則〕も成立します。
正しい原則による解決
落下の力学的説明
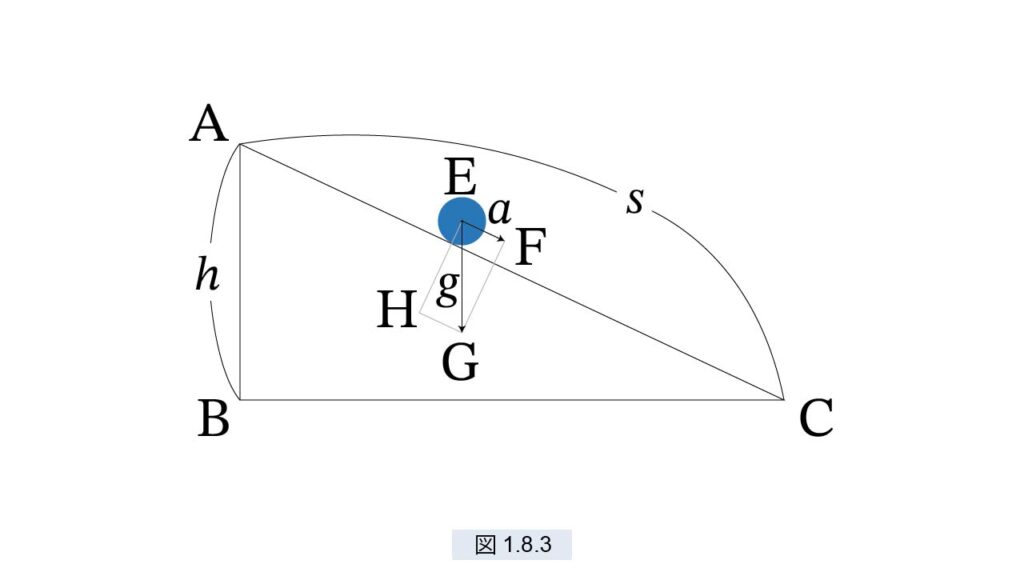
ここで少し力学的なお話をしましょう。ガリレオは落下する物体が速度を増すのは地球に引かれているためだと考えました。しかし、これを理論としてまとめたのはニュートンなので、ニュートンの用語を用いて説明します。図1.8.3 では坂 AC 上に球 E があり、C に向かって落ちています。球 E は重力 g で鉛直に引かれます。これを EG で表します。EGは、球が滑り落ちるのに使われる力 EF と、坂を垂直に押す力 EH に分割されます。
\(EG = g, EF = a, AB = h, AC = s\)
とおくと、△FEG と △BAC が相似であることから
\(a : g = h : s\)
が成立します。これは上で述べた式 (5) にほかなりません。
瞬間速度と全体速度
ガリレオは長い間、等加速度運動において「速度は距離に比例する」という「誤った原則」に囚われていました。しかし、「速度は時間に比例する」という事実に気づくとすべてが一挙に解決しました。それではガリレオが言っていた“瞬間速度”と“全体速度”はどのようになったのでしょうか。
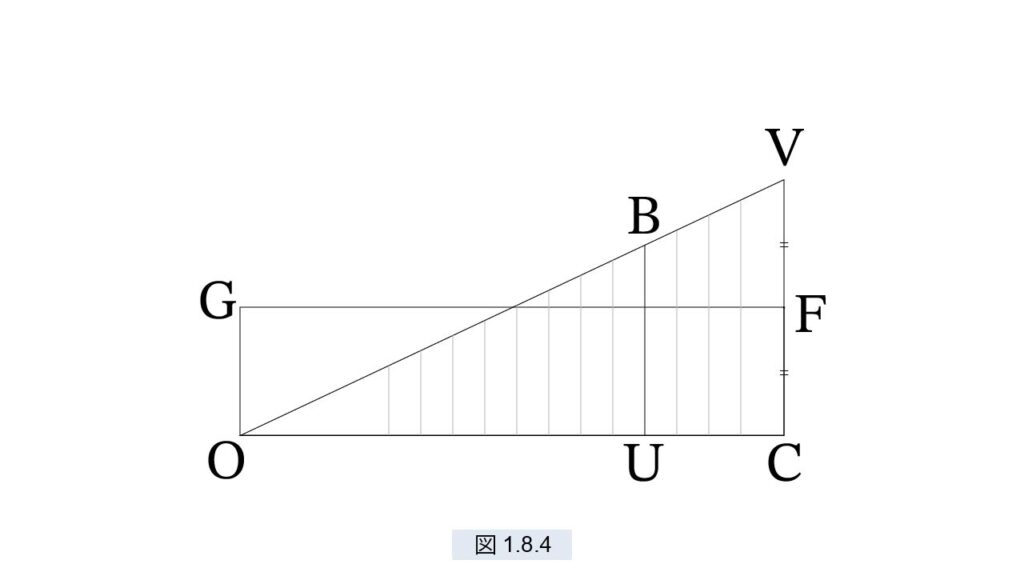
図1.8.4 を考えます。OC は時間軸で、直線 OV は速度を表します。したがって、線分 VC が C における速度です。CV の中点を F とすると、CF がこの落下の中間の速度です。等速運動に関しては、「距離=速度×時間」と定義されていますから、「落下距離=四角形 OCFG」と定めることができます。すると、「三角形VOC=四角形 OCFG」ですから、「落下距離=三角形 VOC」と進みます。ここまでの議論はこれでよいのですが、そのあと以下次のように進みます。
三角形 VOC はVCと平行な無限個の線分 UB からなるとガリレオは考えました。点Uは線分OC上を動きます。この無限個ある線を集めると面になる、と考えたのです。以前は線分を“瞬間速度”、面を“全体速度”としていましたが、今度は面を“距離”としたのでしょうか。いずれにしても、この論法には大きな欠点があります。線の幅はゼロです。ゼロはいくら集めてもゼロのままです。それに速度を集めるとなぜ距離になるのでしょうか。ガリレオの存命中はこの説明がなされていませんでした。
後継者たちによる解決
この議論はガリレオの後継者たちによって、次のように解決されました。ガリレオが手本としたアルキメデスの論法を参考にしたのです。底辺 OC を細かく分割し、△OCV を細い短冊に切り分けました。実際に足されるのは、線分ではなく極微の幅 Δt を持つ短冊 □(Δt, UB) なのです。Δt は非常に小さいので、線分とは見分けがつきません。また、UB は速度でも Δt は時間ですから、短冊は距離となります。したがって短冊の和である △VOC の面積は距離となります。
ガリレオは、速度に数値を割り当てることはしませんでしたが、速度を
距離 = □(時間, 速度)
を満たす量として定義しました。つまり距離は、時間を底辺、速度を高さとする長方形の面積としたのです。長方形の面積の場合、
高さ = 面積/底辺
定義できます。ほどなくして
速度 = 距離/時間
と、数値が計算されるようになります。

