速度の発見

ガリレオが見出した速度の法則

落下の理論に現れる３つの量

〔ガリレオの実験 – 大砲の水平発射・振り子の実験〕の最後で述べた「高台と坂の実験」で、「落下の理論」に必要なデータはすべてそろっています。読者の皆さんのなかには、これですぐに解決すると考えた方がいるかもしれませんが、それは現在の理論を、つまりガリレオたちが作り上げた物理や数学をご存知だからです。落下の理論には、“距離” “速度” “時間”という3つの“量”が現われます。このうちはっきりとしているのは距離だけで、時間はぼんやり、速度に関してはまだ何者か分かっていません。距離に関してもデータとして扱えるのは自然数で表された場合だけです。この節では、ガリレオがどのようにして“速度”という概念を獲得したかを見てみましょう。

 

大砲の発射実験と速度の考察

「高台と坂の実験」でガリレオは〔ガリレオの公準〕を思いつきました（あるいはこの逆かもしれません）。勾配を変えても坂の高さ S が同じなら、球の飛距離は変わらないのです。〔ガリレオの公準〕とは、「坂の高さが同じなら、勾配が違っていても麓(ふもと)での “速度”が同じになる」というものです。つまり速度を飛距離で測れると考えました。

また 〔ガリレオの実験 – 大砲の水平発射・振り子の実験〕で述べた大砲の発射実験では、高台から大砲を水平に発射した場合、火薬の量にかかわらず着地するまでの時間は一定でした。「同じ時間なら、飛距離が速度を表すのではないか」とガリレオは考えました。「高台の高さはどうしたらよいか？高さが変われば飛距離も変わってしまう。」「いっそのこと高台の高さを 0 にし、B から先を水平運動にしてみよう。」 そこで発見したのが次の事実です。

倍距離則

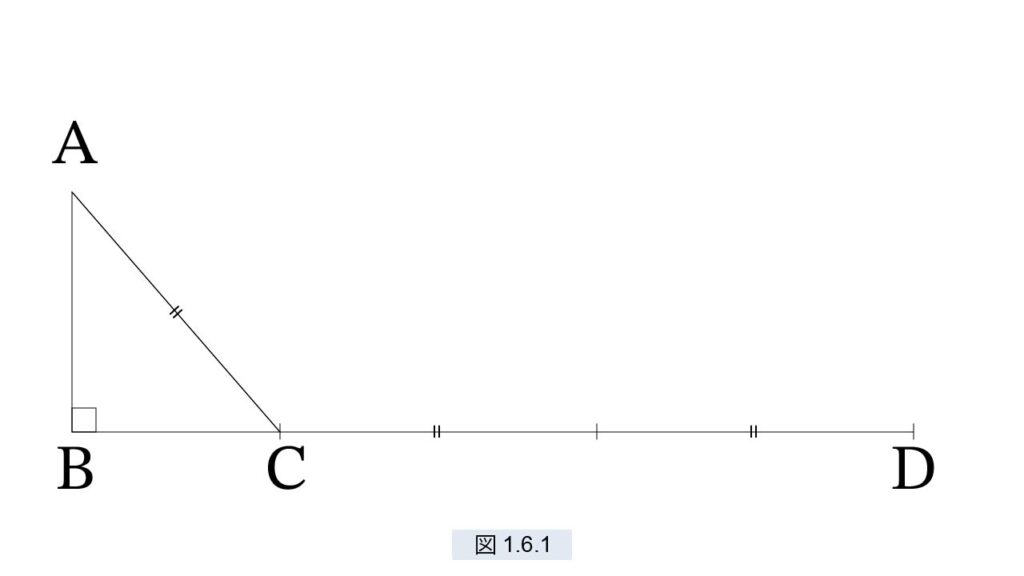
図1.6.1 のように、△ABC の A から球を転がします。BC の延長線上に点 D を、CD ＝ 2AC となるように取ります。すると、次が成立します。

AC に要する時間  ＝  CDに要する時間

この実験は簡単に実現できます。球を2つ用意し、最初の球をA から転がし、C に達したとき2番目の球を A から転がします。最初の球が D に達したちょうどそのとき、2番目の球は C に達しするのです。CDでの運動は、速度が変化しない“等速運動”ではないか、とガリレオは考えました。等速運動なら、“速度とは何か”が分かるのでは？ 等速運動のような基本的な概念は、まず最初に考えなければならないことです。しかし、理論の構築ではよくあることですが、著作とか論文に理論をまとめるときなって初めて、もっとも基本的な概念を思いつくということがよくあるものなのです。

ガリレオは等速運動をどのように定義したか

等速運動の定義と定理

読者の皆さんは“等速運動”といわれても、車の運転などでよく経験することで、ごく簡単な概念だと思うでしょう。しかし「速度という言葉を使わずに説明せよ」と言われると、なかなか難しいと思います。ガリレオ等速運動を次のように定義しました。

つまり、t₁ 時間で距離 s₁ 移動し、t₂ 時間で距離 s₂ 移動するとき、もし t₁ ＝ t₂ なら s₁ ＝ s₂ が成立する、という運動です。このように比の理論ではいつも4つの対象を扱わなければならず、議論がとても煩雑になります。ガリレオはこの定義を用いて、次の定理を証明しました。

この定理を式で表わすと次のようになります。等速運動をしている運動体があります。距離 s₁ 行くのに t₁ 時間かかり、距離 s₂ 行くのに t₂ 時間かかるなら次が成立する。

s₁ : s₂ ＝ t₁ : t₂

この定理を証明するには『原論』の「比の理論」が必要となります。ガリレオは比の理論通りに証明を行っていますがなかなか複雑です。ここでは省略しますが、興味のある読者は、〔積分の源流 アルキメデスの求積 2-4 比の理論〕に同様の議論がありますから、参照してください。この定理を等速運動の定義と考えてもかまいません。

２つの等速運動に関する規定

等速運動の定義と定理 は、一つの運動に関するものであって、2つの等速運動の速度の関係に関してはなにも言っていません。2つの等速運動の速度に関しては次のように規定しました。

つまり、同じ時間なら速い方が長い距離進むので「速さの大きさ比は進んだ距離の比とする」としました。これで等速運動に関しては速度が定義できました。しかし、落下では速度が変わります。ガリレオは次のように考察を進めました。

落下運動の法則

落下運動の速度について

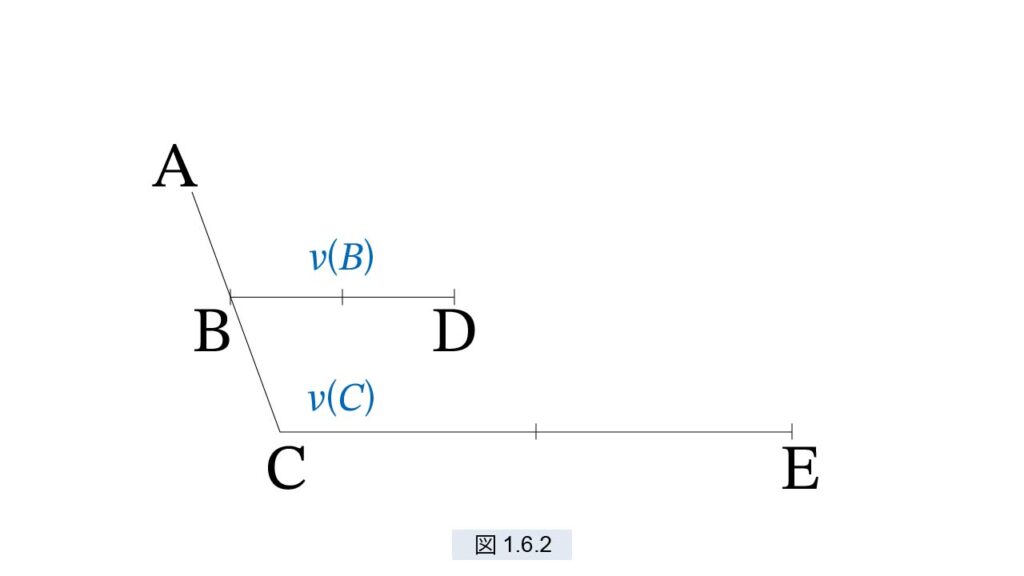
図1.6.2 の坂 ABC におけるA からの2つの落下を考えます。

BD ＝ 2AB, CE ＝ 2AC                                             (1)

とします。最初の落下は B で水平に方向を変え、次の落下は C で方向を変えるとします。

B での速度を v(B), Bまでにかかった時間を t₁,
C での速度を v(C), Cまでにかかった時間を t₂,

2つの落下は、B と C で等速運動になります。したがって〔倍距離則〕より次が成立します。

速度 v(B)、時間 t₁ で距離 BD を移動
速度 v(C)、時間 t₂ で距離 CE を移動

一方、〔時間平方則〕より、次が成立します。

AB : AC ＝ t₁² : t₂²                                                     (2)

分数を使った証明

ここでガリレオは比の理論を使いますが、まず現代の皆さんが使い慣れている分数を使って証明し、その後でガリレオの実際の証明を見てみることにします。

求めたいのは v(B) : v(C) ですが、等速運動の速度の比を求めるためには、上の定義によると、時間を同一にしなければなりません。2番目の等速運動は、CE を時間 t₂ で通過します。CE を点 L で分割し、時間 t₁ で通過する部分を CL とします。つまり、L を

\( CL = CE \times \frac{t_1}{t_2} \)

となるように定めます。すると、

\( v(B) : v(C) = BD : CL = 2AB : ( 2AC ) \times \frac{t_1}{t_2} \)

が成立します。ここで比 a : b を分数 a/b に置き換え、(2) を使うと

\( \frac{v(B) }{v(C) } = \frac{AB}{AC} \times \frac{t_2}{t_1} = \frac{t_1^2}{t_2^2} \times \frac{t_2}{t_1} = \frac{t_1}{t_2} \)

が成立します。これを再び比に直すと

v(B) : v(C) ＝ t₁ : t₂

となります。つまり、落下において「速度は時間に比例する」ことが言えました。

ガリレオの証明

ガリレオはこれをどのように証明したのでしょうか。ガリレオは分数が使えなかっただけではありません。自然数以外の掛け算や割り算が使えなかったのです。したがって、例えば t² は実数 t の2乗ではなく、辺 t を一辺とする平方、すなわち正方形 □²(t) を表したのです。従って (2) は、

AB : AC ＝ □²(t₁) : □²(t₂)                                         (3)

と表されます。ただし、□²(t₁) と □²(t₂) は具体的な面積で与えられているわけではないので、

t ₁ :  t₂ = AB : AS  

を満たす線分を作図しなければなりませんでした。この作図には次の図を使います。

線分 AB と AC の比例中項を AS とします( 図1.6.3 )。つまり、AB : AS ＝ AS : AC とします。すると、〔内項外項〕の定理 より

□(AB, AC) ＝ □²(AS)

が成立します。すると、

AB : AC ＝ □(AB,AB) : □(AB, AC)
＝ □²(AB) : □²(AS)

となり、(3) より

□²(t₁) : □²(t₂) ＝ □²(AB) : □²(AS)

が成立します。よって

t₁ : t₂ ＝ AB : AS                                                      (4)

が成立します。つまり、時間の比が具体的な線分の比として表すことができたのです。線分 CE 上に点 L を、

CL : CE ＝ AB : AS                                                      (5)

となるように取ります。すると、

CL : CE ＝ t₁ : t₂

となります。A から落下した球が、C で水平方向に向きを変え、速度 v(C)、時間 t₂ で CE を通過します。CL を通過する時間は t₁ で、速度 v(B) で BD を通過する時間と同じです。よって

v(B) : v(C) ＝ BD : CL                                           (6)

が成立します。これで、速度の比 v(B) : v(C) が、長さの比 BD : CL で表せました。このあとは、この比が t₁ : t₂ となることを比の理論を使って証明しています。比の理論の技術的な熟練が必要ですから読み飛ばして結構です。AS は AB と AC の比例中項だから AB : AS ＝ AS : AC ですから、右項と左項をひっくり返すと

AS : AB ＝ AC : AS

が成立します。したがって (1) と (5) より次が成立します。

BD : CE ＝ AB : AC
CE : CL ＝ AS : AB ＝ AC : AS

この2式を、分数と思って辺々掛け合わせると（前節で述べた比の掛け算）、

BD : CL ＝ AB : AS

となります。よって (6) より

v(B) : v(C) ＝ AB : AS

が得られ、(4) より

v(B) : v(C) ＝ t₁ : t₂

が得られます。

ガリレオは20年以上にもわたる「落下における速度は距離に比例する」といった「誤った原則」をさまよったのち、とうとう「正しい原則」にたどり着きました。定義と定理としてまとめておきます。