ピタゴラスの定理 とは

ピタゴラスの定理（三平方の定理）とは？

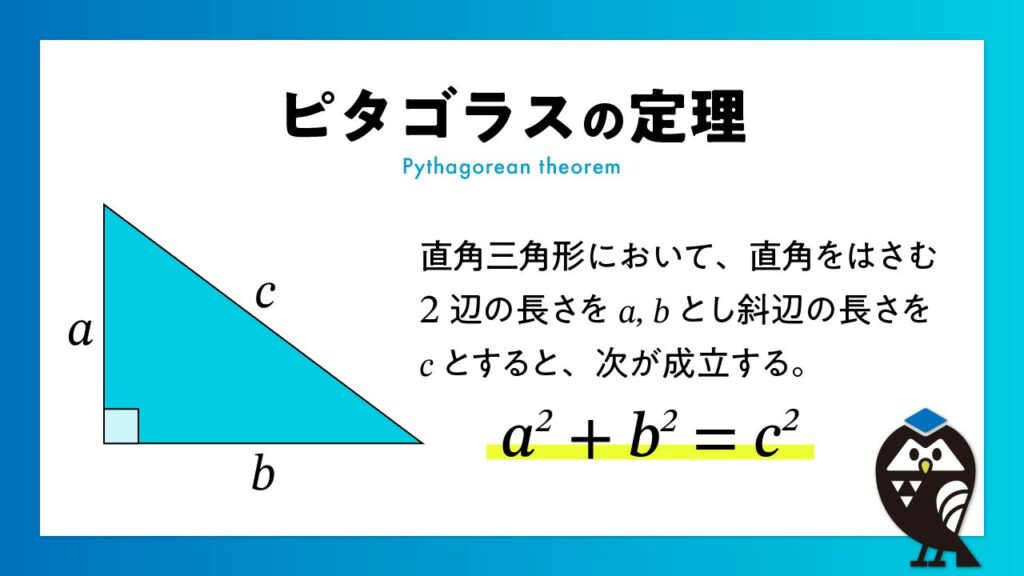
ピタゴラスの定理（三平方の定理）は、直角三角形の性質を表す基本的かつ有名な定理です。数学が苦手な人でも、一度は聞いたことがあるのではないでしょうか？この定理の内容はとてもシンプルです。

「直角をはさんでいる2辺（直角の両側）の長さを2乗して足すと、斜めの辺（斜辺）の長さの2乗と等しくなる」

これを数式で表すと、次のようになります。

a² + b² = c²

ここで、
・a と b は直角をはさむ辺（直角三角形の底辺と高さ）
・c は斜辺（直角の向かいの辺）
という関係になります。

ピタゴラスの定理には、逆も成り立つという重要な性質があります。

三角形の3辺の長さa, b, cとしたとき、a² + b² = c² が成り立つなら、その三角形は「c を斜辺とする直角三角形」になります。
この性質は、三角形が直角三角形かどうかを確かめるときにも使えます。

ピタゴラスの定理は、三角形の2辺の長さが分かっているときに、残りの1辺の長さを求めるのに使います。例を見てみましょう。

例題
一辺が 3cm、もう一辺が 4cm の直角三角形があります。このとき、斜辺の長さはいくつでしょうか？

解き方
斜辺の長さをxとし、ピタゴラスの定理に当てはめます。
3² + 4² = x²
x² = 9 + 16
x² = 25
x = 5
斜辺の長さは5cmです。このようにピタゴラスの定理を使うと、簡単に長さが求められます。

ピタゴラスの定理の証明

ピタゴラスの定理には、実に100通り以上の証明方法があるといわれています。ここではその中でも特に直感的で、図形を使って理解しやすい証明をひとつ紹介しましょう。

図形で考える証明

まず、1辺が c の正方形（水色）を描き、そのまわりに、底辺が b、高さが a の直角三角形（青色）を4つ配置します。

すると、全体として 1辺が a + bの大きな正方形が出来上がります。

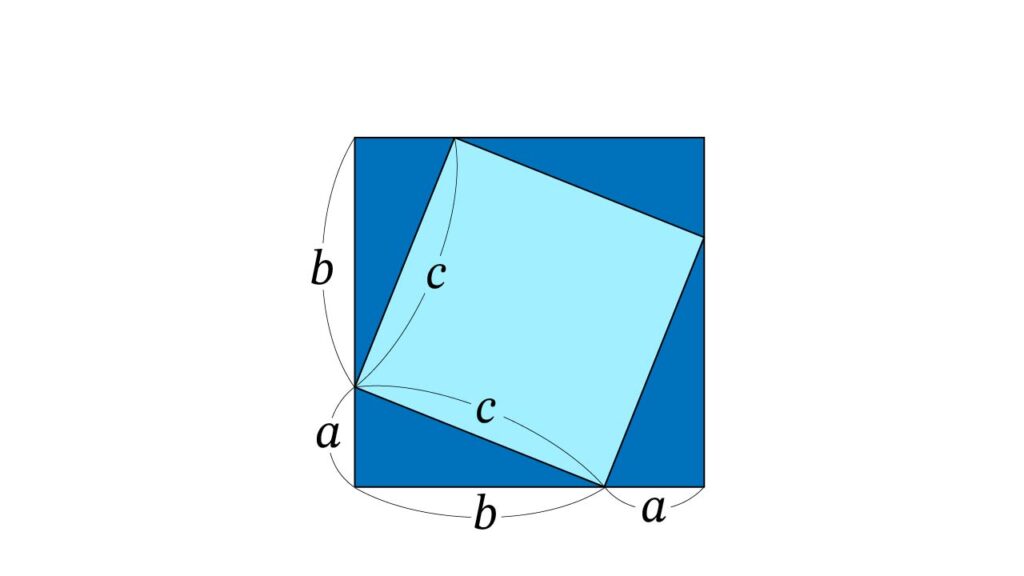
この図形からわかること

• 外側の大きな正方形の面積は： (a + b)²
• この正方形の中には：
  • 中心部分に面積 c² の小さな正方形（斜辺を1辺とする）が入っています
  • 面積ab/2 の直角三角形が4つ

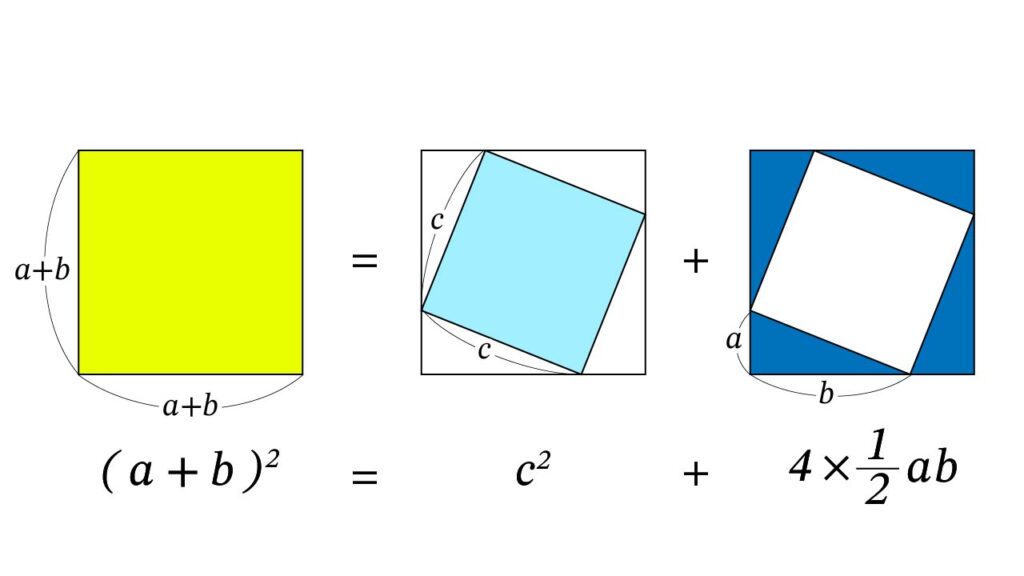
外側の大きい正方形（黄色）の面積は1辺が a + bの正方形なので面積は( a + b )² です。これは1辺が c の正方形（水色）と底辺が b 高さが a の直角三角形 4つ（青色）の和です。式で表すと、以下のようになります。

( a+ b )² = c² + 4 × 1/2 ×ab
a² + 2ab + b² = c² + 2ab
a² + b² = c²

このように、図形の構成と面積の関係から、ピタゴラスの定理が自然に導けるのです。

ピタゴラス数（ピタゴラスの三つ組）とは？

「 a² + b² = c²  」
という関係を満たす3つの自然数 a, b, c の組み合わせを、ピタゴラス数 または ピタゴラスの三つ組（ピタゴラスの3つ組） と呼びます。

この3つの数 (a, b, c) を辺の長さとする三角形を作ると、それは必ず 直角三角形 になります。

最も基本的なピタゴラス数

もっともよく知られたピタゴラス数は：
(3, 4, 5)
この組み合わせは、元祖ピタゴラスの3つ組とと呼ぶ人もいます。

他にもあるピタゴラス数の例

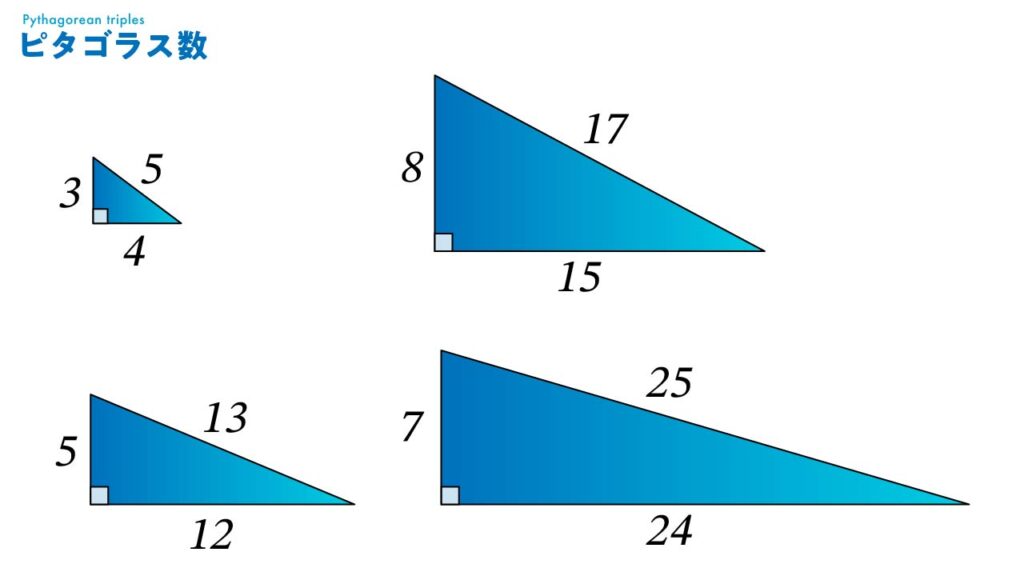
• (5, 12, 13)
• (7, 24, 25)
• (8, 15, 17)

ピタゴラス数には無数に存在することが知られており、数学ではこれらの数列の特徴を使ってさまざまな応用が行われています。

ピタゴラスの定理の歴史と古代エジプトの測量術

ピタゴラスの定理として知られる「直角三角形の関係」は、実は古代ギリシアの数学者ピタゴラスが発見するよりもずっと前から、エジプト文明の測量技術に利用されていたと考えられています。

ナイル川の氾濫は、古代エジプトの農業を支える大切な自然現象でした。毎年のように起きる洪水は、上流から肥沃な土壌を運び、土地を豊かにしてくれます。

しかし水が引いたあと、土地の境界線がすべて消えてしまうという問題がありました。このとき登場するのが、「縄師」と呼ばれる測量の専門家です。国全体の耕作地を区画整理して、農民一人一人の持ち分を割り当てたのです。

縄師たちは、3・4・5の比率で印をつけたロープを使い、正確に直角三角形をつくる技術を用いて土地を区画整理しました。

この方法では、ロープを3、4、5の長さに分け、それぞれの印を結んで三角形を作ると、直角がきれいに出るのです。

このように直角三角形の性質は土地の測量に用いられていました。古代エジプト人がピタゴラスの定理を知っていたという証拠は見つかっていません。しかし、(3, 4, 5) の三辺で直角三角形ができるということは実践的な知識として使われていたことが、歴史資料からうかがえます。

このように、ピタゴラスの定理は「発見された定理」というより、人類が生活の中で自然に使いこなしてきた法則でもあるのです。

名前の由来となったピタゴラスとは？

古代ギリシアの数学者、哲学者として知られているピタゴラス。ピタゴラスは、数には神秘的な力があると信じ、この世界は数によって支配されていると考えていました。ピタゴラスには様々な逸話が残されています。詳しく知りたい方はぜひ以下をご一読ください▼

古代ギリシアの数学者『ピタゴラス』のお話[Vol.1]

古代ギリシアの数学者『ピタゴラス』のお話[Vol.2]

現代の私たちは、長さ、面積、体積、角度などを数で表しています。古代ギリシア人も私たちと同様だと思いがちですが、実はそうではありません。古代ギリシア人にとって数とは個数を表わす自然数だけだったのです。〔Web連載ピラミッドの謎：4-2.ピタゴラスの定理〕ではピタゴラスの定理を古代ギリシアの概念だけを使って考えます。

まとめ

• ピタゴラスの定理は、「直角三角形において、斜辺の長さの2乗は、他の2辺の2乗の和に等しい」という定理です。 　数式では a² + b² = c² と表されます。
• 最も有名なピタゴラス数は (3, 4, 5)$で、この3つの数を辺とする三角形は直角三角形になります。
• 古代エジプトでは、測量のためにこの「3:4:5の関係」を実用的に利用しており、ピタゴラスの定理に近い性質がすでに生活の中で活かされていました。
• ピタゴラスの定理には100通り以上の証明方法が存在し、そのうちのひとつは図形（正方形と直角三角形）を使った直感的な証明です。
• この定理は古代から現代に至るまで、数学だけでなく建築・物理・工学など幅広い分野で活用されています。

ピタゴラスの定理は、シンプルでありながら奥深い幾何学の基本。

その歴史と多彩な活用例を知ることで、数学がより身近に感じられるようになるはずです。