トレミーの定理 とは

トレミーの定理とは

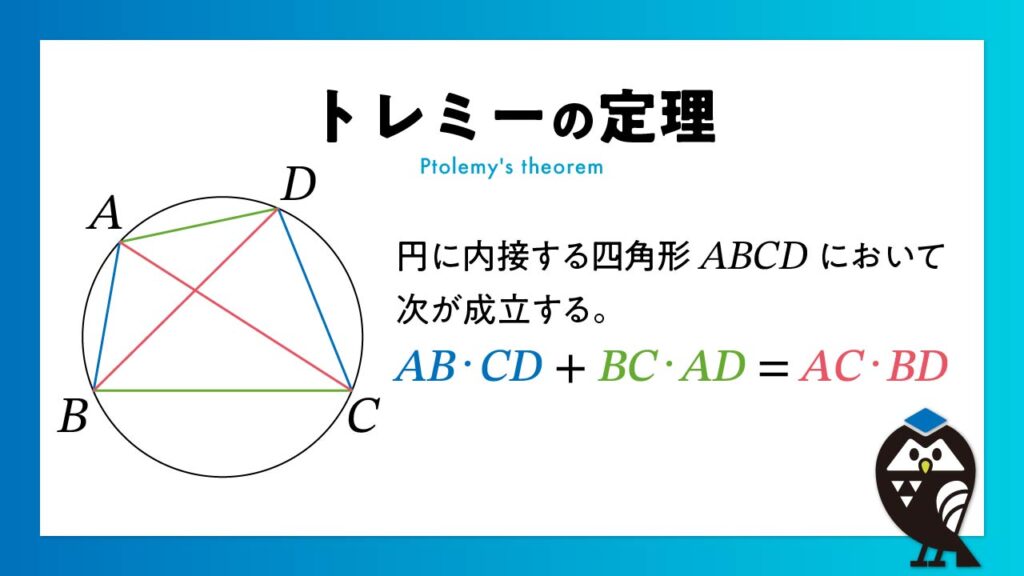
トレミーの定理は、円に内接する四辺形における辺と対角線の長さの関係を示す幾何学の定理です。

四辺形 ABCD が円に内接しているとき、次の式が成り立ちます：

AB × CD + BC × AD = AC × BD

これは、

「向かい合う辺の積の和は、対角線の積に等しい」

という関係を表しています。

シンプルながら強力なこの定理は、円と多角形の性質を扱うさまざまな場面で応用されています。

トレミーの定理の証明

この式を証明するために、点 E を対角線 BD 上に取り、補助線を引きます。

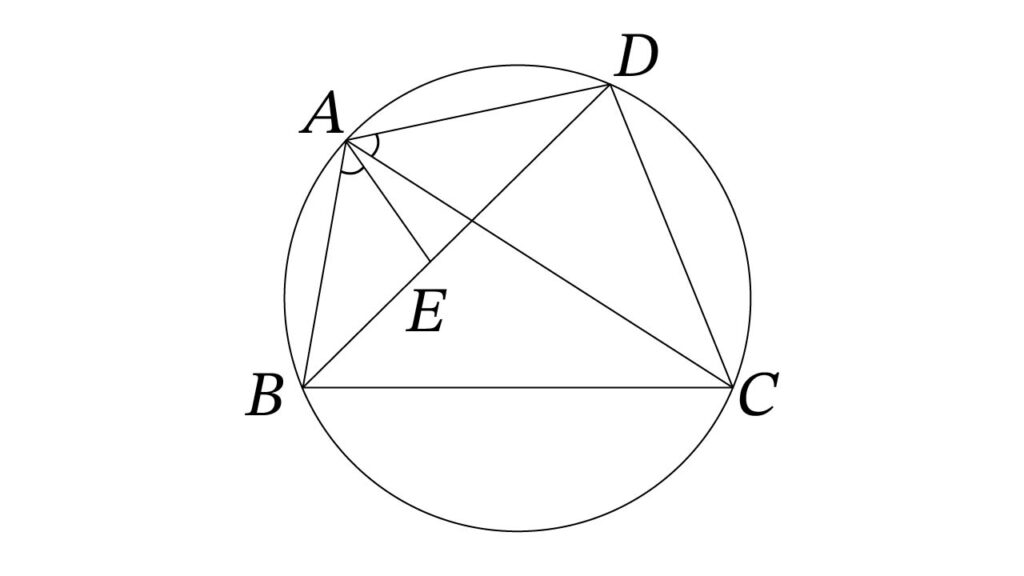
① 点 E の設定

上の図のように、対角線BD上に∠BAE = ∠CADとなるように点Eをとります。

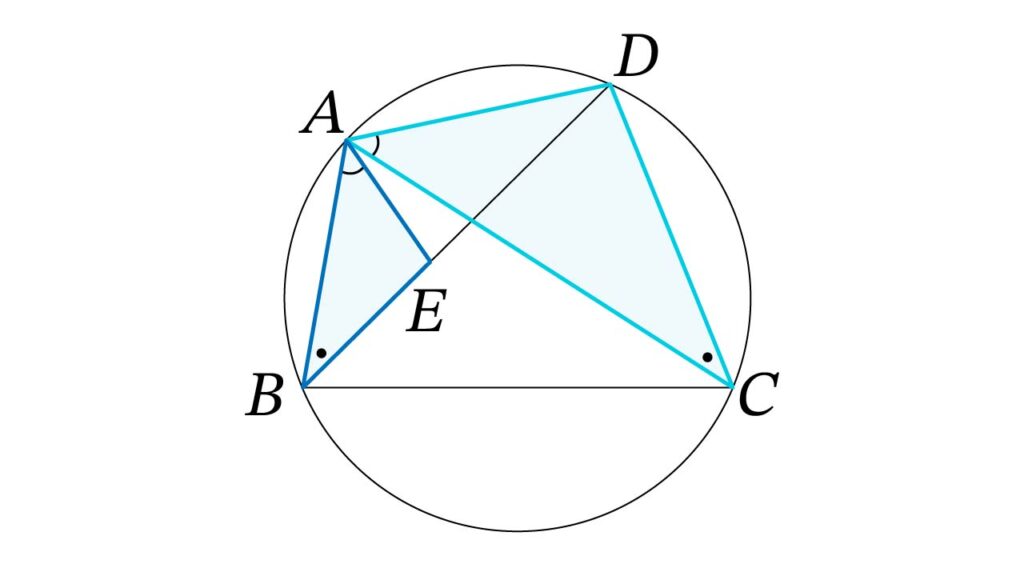
② 三角形 ABE と ACD の相似

• 円周角の定理（同じ孤に対する円周角は等しい）より、 ∠ ABE =∠ACD
• さらに仮定より、 ∠ BAE = ∠ CAD

２組の角がそれぞれ等しいので三角形ABEと三角形ACDは相似です。

よって

AB : BE = AC : CD
AB・CD = AC・BE　　(1)

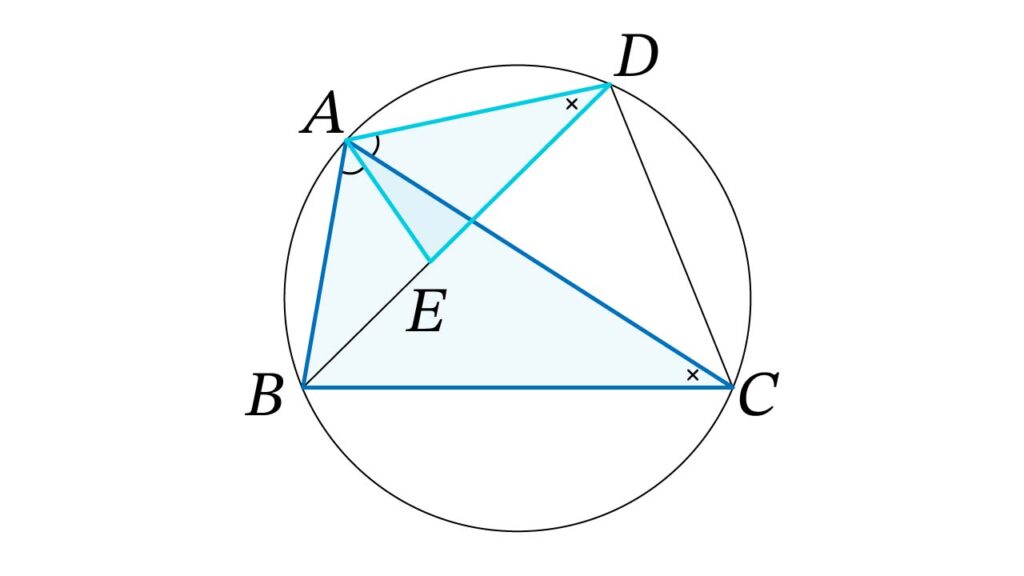
同様に円周角の定理より∠BCA = ∠EDA。∠BAC = ∠EADなので三角形ABCと三角形AEDは相似です。

よって

AC : BC = AD : DE
AD・BC = AC・DE　　(2)

(1)(2)の式を足すと

AB・CD + AD・BC = AC・BE + AC・DE
AB・CD + AD・BC = AC・( BE + DE )

ここで、点 E は BD 上の点なので、

BE + DE = BD

したがって、

AB・CD + AD・BC = AC・BD

が証明されました。

このように、円に内接する四辺形の辺と対角線の関係を巧みに利用することで、トレミーの定理が導かれるのです。

名前の由来となったトレミー（プトレマイオス）とは

「トレミーの定理」の名前の由来であるトレミー（Ptolemy）は、2世紀にアレクサンドリアで活躍したギリシア系の天文学者・数学者・地理学者で、本名はクラウディオス・プトレマイオスです。

彼は著作『アルマゲスト』において天動説（地球中心説）を体系的に説明し、中世ヨーロッパからイスラム世界にかけて長らく天文学の権威とされました。また、幾何学や三角法にも精通し、『アルマゲスト』の中でトレミーの定理を証明したことから、この名が残されています。

ピタゴラスの定理との関係

トレミーの定理は、円に内接する任意の四辺形に成り立ちますが、特にその四辺形が長方形である場合に注目してみましょう。

下の図のように、長方形の隣り合う辺の長さを a と b、対角線の長さを c とすると、トレミーの定理により次の関係が得られます：

a² + b² = c²

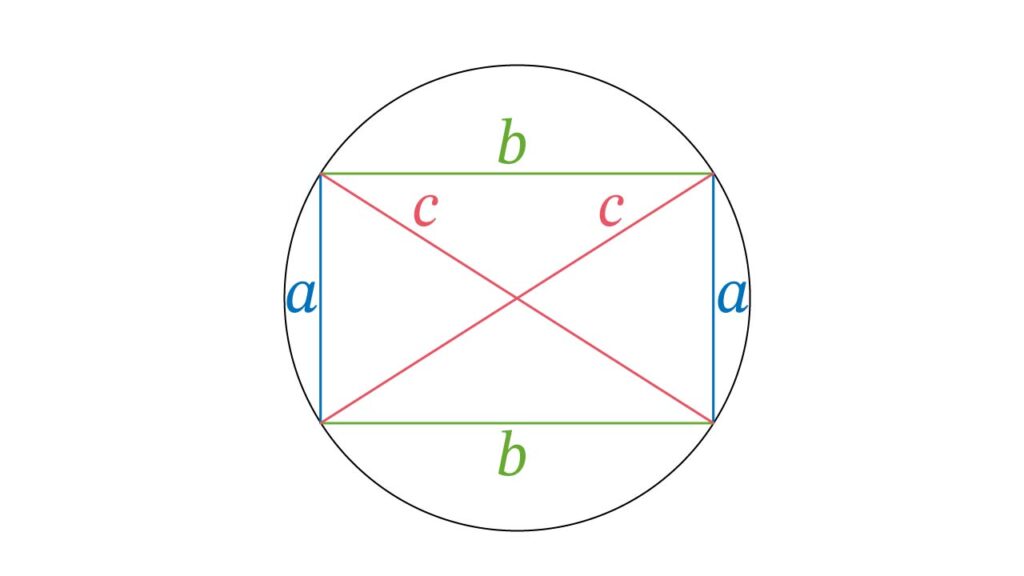
これはまさにピタゴラスの定理と一致します。

つまり、ピタゴラスの定理はトレミーの定理の特別な場合と見ることができ、トレミーの定理はピタゴラスの定理のより一般化された形といえるのです。

まとめ

トレミーの定理は、円に内接する四辺形において「向かい合う辺の積の和が対角線の積に等しくなる」という美しい関係を示す定理です。

幾何学的な性質の深さだけでなく、ピタゴラスの定理の特別な場合としても導けることから、古代から現代に至るまで広く応用されています。

この定理を記したのが、2世紀のギリシア人学者プトレマイオス（トレミー）であり、天文学と数学の発展に多大な影響を与えました。

トレミーの定理を通じて、図形のもつ調和と数学の奥深さを感じてみてください。