素数 とは

素数(prime number)とは

素数（prime number）とは 1 と自分自身以外に約数を持たない自然数のことです。
最も小さい素数は「2」で、唯一の偶数の素数でもあります。

たとえば、1から100までの素数には以下のような数があります：
2、3、5、7、11、13、17、19、…
全部で25個存在します。

古代ギリシアにおける素数の考え方

古代ギリシアの数学では、数を「小石を並べた形」で分類していました。たとえば：

• 2列にぴったり並べられる数は「偶数」
• 2列に並べると1つ余る数は「奇数」

このように、数に形を対応させて分類し、概念を生み出すことが、当時の理論の始まりでした。

「長方形にできるか」で数を分類

ギリシア人は、数が長方形の形に並べられるかどうかを重要視していました。

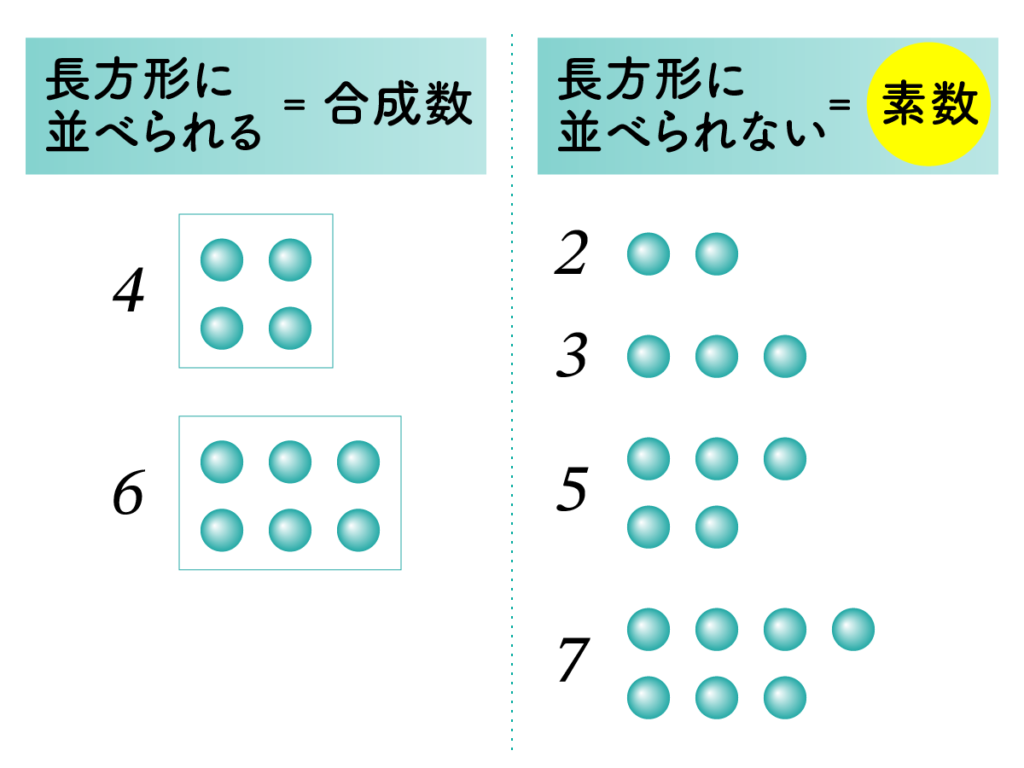
• 4、6、9のように、2つ以上の行と列に並べられる数は 長方形数 と呼ばれました（ただし1列のものは除く）。
• 現代の言葉でいえば、これは 合成数 に相当します。

反対に、長方形に並べることができない数──つまり正方形にも長方形にもならない数が、ギリシア人にとっての「素数」でした。

例：

• 2、3、5、7などは、どのように小石を並べても長方形を作れないため、素数とされました。

数を「形」で分類した古代ギリシア人の考え方

古代ギリシアでは、数を「小石を並べてできる形」によって分類していました。

たとえば──

• 2列にきれいに並べられる数は「偶数」
• 2列に並べると1つ余る数は「奇数」

このように、見た目や形に基づいて数を分類し、新しい言葉（概念）を作り出すことが、当時の数学における「理論の始まり」だったのです。

素因数分解とは?

自然数のうち、素数以外の数（＝合成数）は、いくつかの素数をかけ合わせることで表すことができます。このように、数を素数の積に分解することを「素因数分解」といいます。

合成数と長方形数の関係

合成数とは、1 以外の 2 つ以上の自然数の積として表される数のことです。

たとえば、ある合成数 a が b と c の積として表されたとします。このとき、小石を b 行 c 列に並べれば、長方形の形ができます。

このように、合成数 = 長方形に並べられる数という発想は、古代ギリシア人の特徴的な考え方で、彼らは合成数のことを「長方形数」と呼んでいました。

もし b や c のどちらかがさらに合成数だった場合、それもまた別の数に分解できます。これを繰り返していくと、最終的には素数の積にたどり着きます。

ここで登場する素数は、合成数の因数であることから「素因数」と呼ばれます。そして、ある数を素因数の積として表す操作が「素因数分解」なのです。

古代ギリシア人はなぜ素数に魅了されたのか？

古代ギリシア人をはじめ、古代の人々は数そのものに神秘的な意味や力が宿ると信じていました。たとえば、ある合成数 a = b × c は、単なる積ではなく、数 b と c の「意味」や「力」が合わさったものだと考えられていたのです。

同様に、

• 平方数 a² は、数 a の力が「2倍」に強められたもの
• 立方数a³ は、「3倍」の力を持つもの

といった解釈もなされていました。

こうした思想の中で、どんな数の積にも分解できない「素数」は特別な存在とされます。

それは、他の数に依存せず独立して存在する、純粋で唯一の意味を持つ数──まさに、分解できない「始原的な数」として、特別な神秘性を帯びていたのです。

美しい証明：素数は無限に存在する

「素数は無限に存在する」──

この事実は、古代ギリシアの数学者ユークリッドがその著書『原論』の中で示したもので、

のちの時代の数学者たちから「もっとも美しい証明の一つ」と称賛されています。

証明の流れ

まず、素数は有限個しかないと仮定してみます。

すべての素数を並べたとき、それが

p₁, p₂, p₃, …, pₖ

の k個しか存在しないとしましょう。

このとき、新たな数：

a = p₁ × p₂ × p₃ × … × pₖ + 1

という数 aを考えます。この a は、すでにあるすべての素数で割り切れない数です。

なぜなら、どの p_i で割っても 1余るからです。

つまり、a はこれらの素数のどれでも割り切れません。

• a が素数であれば、これは「新しい素数」です。
  → もとの素数リストには含まれていなかった素数の登場＝仮定と矛盾。
• a が合成数であっても、 その約数の中には必ず「素数の約数」が含まれます。 しかしその素数も、もとのリストには含まれていません。

このように、

「素数は有限個しかない」と仮定すると矛盾が生じるため、

結論として：

素数は無限に存在する。

ということが論理的に導かれるのです。

エラトステネスのふるい

「エラトステネスのふるい」は、ある範囲内の素数を効率的にまとめて見つける方法です。
現在でも、小学生からプロの数学者まで広く使われている、シンプルかつ強力なアルゴリズムです。この方法の名前は、古代ギリシアの学者 エラトステネス に由来しています。

エラトステネスってどんな人？

エラトステネスは、ヘレニズム時代を代表する知識人であり、数学・天文学・地理学など、あらゆる分野で活躍した古代ギリシアの大科学者です。

とくに有名なのが、「地球の周の長さ（周長）」を初めて測った人物だとされています。

まとめ

• 素数とは「1と自分自身以外に約数を持たない自然数」であり、合成数とは対をなす概念です。
• 古代ギリシア人は数に形や意味を見出し、特に素数には神秘的な価値を感じていました。
• ユークリッドは「素数が無限に存在すること」を美しい論理で証明し、現代にまで語り継がれています。
• 「エラトステネスのふるい」は、簡単な操作で多数の素数を効率的に見つけられる古典的なアルゴリズムです。

素数は単なる数ではなく、理論・歴史・哲学が交差する特別な存在です。

そしてその探求は、今も続いています。