エラトステネスのふるい とは

エラトステネスの篩（ふるい）とは？

エラトステネスのふるいは、古代ギリシアの学者エラトステネスが考案した、素数を見つけるためのシンプルで効率的な方法です。

素数とは「1と自分自身以外に約数を持たない自然数」のことで、数学の世界ではとても重要な役割を持ちます。

この方法では、一定範囲の自然数を並べ、最小の素数から順にその倍数をふるい落としていくことで、素数だけを残していきます。

エラトステネスのふるいで50までの素数を見つけよう

例えば50以下の素数を全て求めてみましょう。下の図のように1から50までの数を書き、1から順に素数でないものを消していきます。素数以外の数をふるいにかけて落とすイメージです。

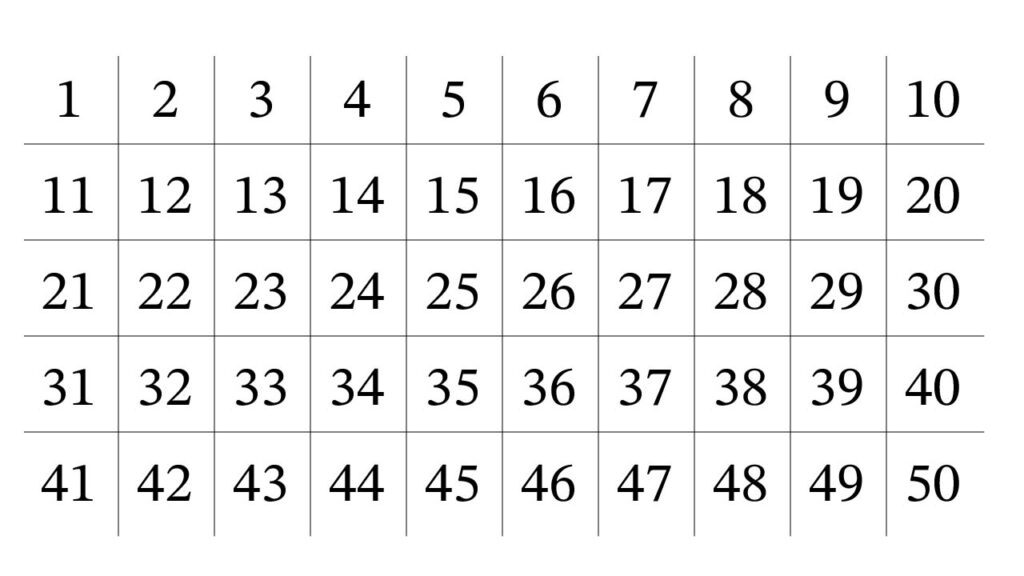
まず 1 は素数でないから消します。次に最初の素数2を残し、2の倍数（4, 6, 8, … 50）を全て消します。これらは2を約数として持つので素数ではありません。

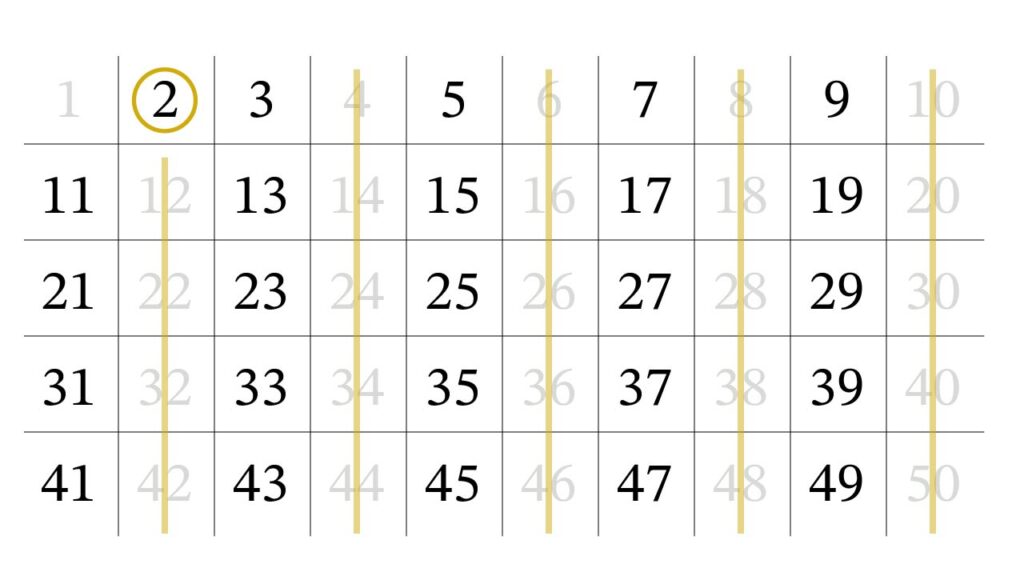
次に進むと3に出会います。3は素数なので残し、3の倍数を全て消します。

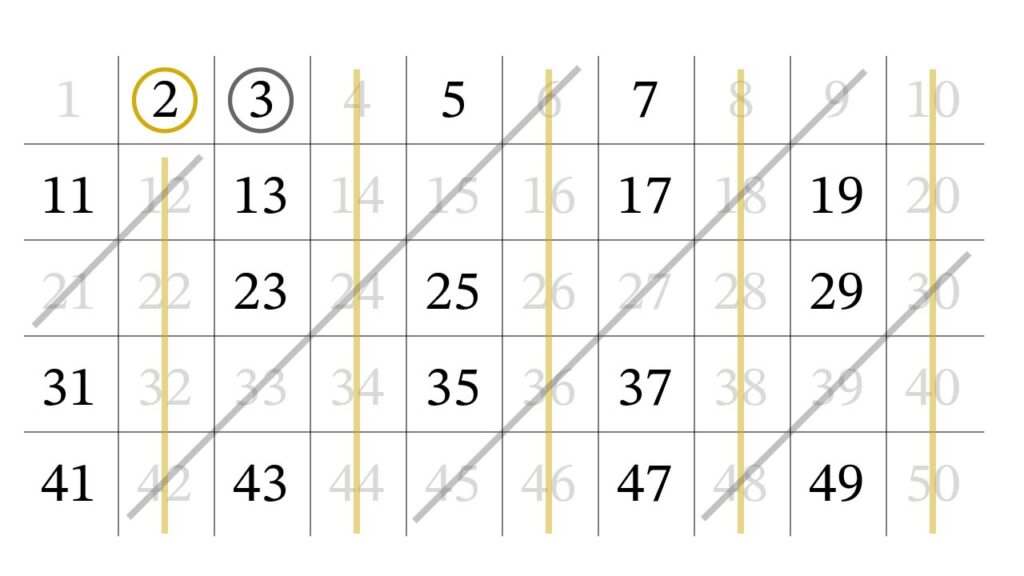
次に進むと5に出会います。5は素数なので残し、5の倍数を全て消します。

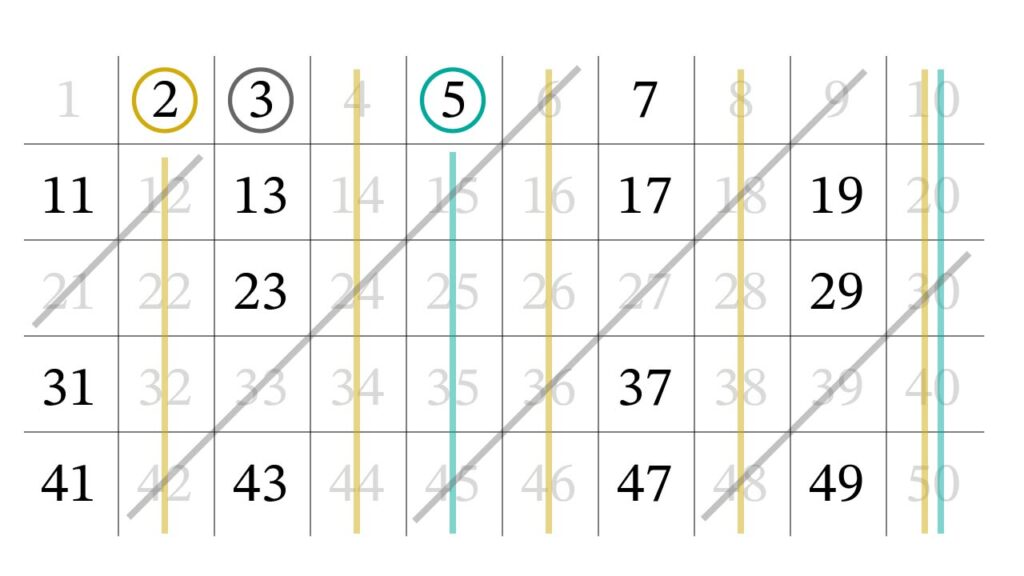
この操作を続けると以下の数が消されずに残り、素数を見つけることができます。

2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47

エラトステネスのふるいは、素数を効率的に見つける手順、つまりアルゴリズムです。今日では当たり前のように知られているこの方法は、実は「素数表」を作るための非常に実用的な手段として、長いあいだ数学者に重宝されてきました。

しかし、素数の研究そのものは長い間「役に立たない理論」と見なされていました。素数は数論という分野を築くきっかけにはなりましたが、実用性は乏しいと考えられていたのです。

状況が一変したのは20世紀に入ってから。コンピュータの発展とともに、素数は情報セキュリティの根幹を支える存在となりました。とくに暗号技術の分野では、素数がなければ安全な通信は成り立ちません。こうして、かつては“遊び”とさえ思われていた素数研究が、現代社会のインフラを支える重要な基盤となったのです。

なお、「エラトステネスのふるい」という名称は、後世の誰かが彼の名をこのアルゴリズムに結びつけた可能性もあります。確かなことは、この単純なふるい分けの考え方が、素数研究の出発点として今なお価値を持ち続けているということです。

素数に関する解説はこちら▼

名前の由来となったエラトステネスとは

エラトステネスは、紀元前3世紀の古代ギリシアの天文学者・地理学者で、エジプト・アレクサンドリアにあった有名な大図書館の館長を務めていました。

彼は、地球の大きさ（周長）を初めて正確に測定しようとした人物として知られています。

また、素数を効率よく見つける「ふるい法（エラトステネスのふるい）」を考案したことでも知られ、その功績は現代の数学やコンピュータ科学にも影響を与えています。