
指数関数とは?曽呂利新左衛門の話に学ぶ驚きの数の増え方
指数関数とは
古代人の数に関するお話の中には、倍、倍、倍と何度も2倍を繰り返すと、とてつもなく大きな数になるというお話がよくあります。まず、指数関数の説明をしておきましょう。
数aの2乗はa×a、3乗はa×a×a、一般にaのn乗はaをn個掛けたものです。aのn乗を指数関数といいます。

ネズミ算…倍々に増えていくと?
もちろん指数とか関数などという概念は古代にはありませんが、次のような数列はいろいろな古代文明の文書史料に出てきます。
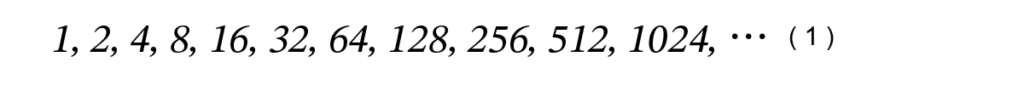
たとえば、一つがいのネズミが一晩に一つがいの子供を産むとします。二日目は2つがい、3日目は4つがいと増えていきます。「30日後には何つがいになるでしょうか」という問題です。答えは、”2の30乗”つがい、約 10億つがいとなります。いわゆるネズミ算です。これと同様のお話は、エジプトや古代インドや中国などにもありますから、おそらくどこにでもあったのだと思います。
秀吉と曽呂利新左衛門
日本のお話を紹介しておきましょう。むかし秀吉のお伽衆の一人に曽呂利新左衛門という知恵者がいました。あるとき秀吉から褒美をもらえることになりました。「何でも好きな褒美をやろう」と言われます。新左衛門は将棋盤を前に置き、次のように答えたそうです。「最初の日はお米一粒をもらいます」といって、将棋盤の端のます目にお米一粒を置きます。「次の日は、前日の二倍の二粒をもらいます」といって、次のます目に二粒のお米を置きます。「このようにして毎日前日の2倍のお米を、ます目の数だけの日数、つまり81日間もらいたいと思います」
秀吉はなんて欲のない男だと思いました。果たしてそうでしょうか。新左衛門はどれくらいのお米をもらえるのか、実際に計算してみましょう。
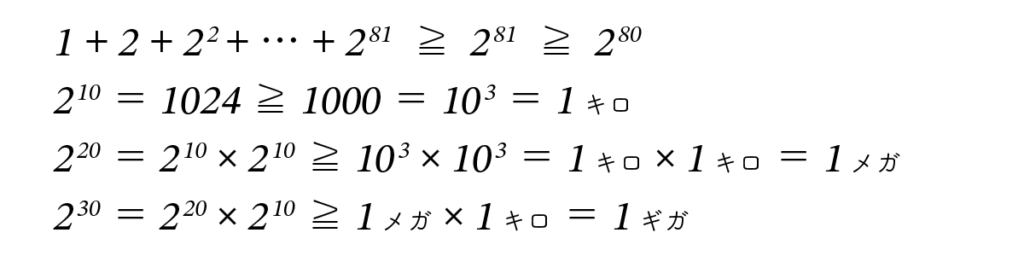
最初はたった一粒のお米でも、倍々…に増えていくと恐ろしい数になることがわかる逸話です。
数列、級数
数列 (1) はコンピュータではよく現れるので、次のように「ニ、ヨン、ハチ、イチロク、ザンニ、ロクヨン、イチニパ、ニゴロ、ゴイチニ」のように暗記しておくと便利です。また、以下の関係を覚えておくと、だいたいの数を見積もることができます。

数を並べたものを数列といいます。また数列の和を級数といいます。指数を使って (1) の数列を書き換えると次のようになります。古代にはゼロはありませんが、aの0乗は1と定められています。

数列 (2) の n 項までの和は次のようになります。
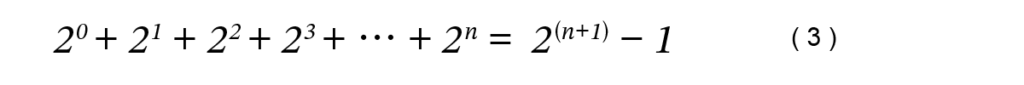
古代の表現方法
古代にはこのような便利な式はないので、すべて言葉で表していました。(3)では「任意の自然数を表す変数n」が使われていますが、古代にはこのような表現方法はないので、常に具体的な数値(たとえば 3 とか 4)を使って表します。それにもかかわらず、古代でも (3) のような公式を理解していたようです。
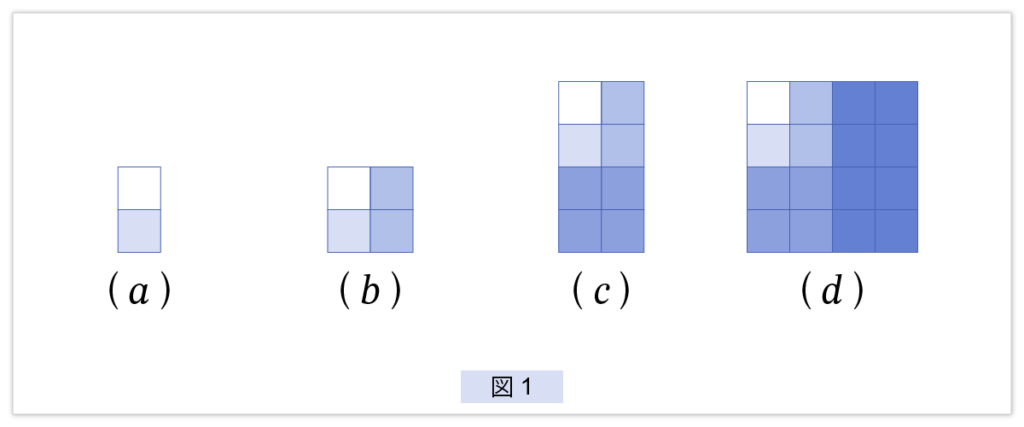
図1 は (3) を図で証明したものです。小さい正方形をマスと呼ぶことにします。マスの個数は (a), (b), (c), (d) で、2, 4, 8, 16 と、倍々と増えていきます。次に、白いマスを除いて考えます。すると、色のついたマスの数は (a) は 1、(b) は 1+2、(c) は 1+2+4、(d) は 1+2+4+8 となります。両方を合わせると、(d) は

を表すことになります。このように古代ギリシアの人々は図形の概念を使って様々な証明を行っていました。




