ガリレオの失敗

ガリレオ・ガリレイは数学において後世に絶大な影響を与えました。本連載では当時の時代背景を踏まえ、ガリレオの残した業績を詳しく調べていきます。ガリレオが速度という概念に辿り着くまでの過程を見てみましょう。

『天文対話』- 地動説の支持で問題となった著作

潮汐現象に関する誤り

ガリレオは数々の実験をして多くの事実を知りましたが、その時点ではまだ「落下の理論」を作り上げていませんでした。最も基本的な“速度とは何か”がはっきり捉えられていなかったのです。得られた理論的な結果は「誤った原則」を基にしたものでした。ガリレオは、「落下の理論」以外にもいくつも誤りを犯しています。 特に重要なのは、ガリレオ裁判で問題となった『天文対話』(1632)という著作です。ガリレオは地動説（太陽中心説）を擁護することを禁じられていましたが、この著書で公然とその禁を破ったのです。その中心となる論旨(ろんし)は「潮汐(ちょうせき)現象」です。ガリレオは著書の中で次のように語っています

宇宙の中心に地球を置く天動説では、海水の横方向への移動である潮汐現象を説明することはできない。しかし太陽のまわりを公転する地動説ならば、自転との運動から説明できる。図のように太陽 S の周りに地球 E が回っているとしよう。地球の公転速度を V、地球の自転速度を v とする。すると、太陽に面した地点 A では太陽の進行方向と自転の方向が逆になるから速度は V – v となり、太陽の裏側の地点 B では、進行方向が同じとなるので速度は V＋v となる。A では海水がゆっくり流れるので満潮になり、B では速く流れるので干潮になる。

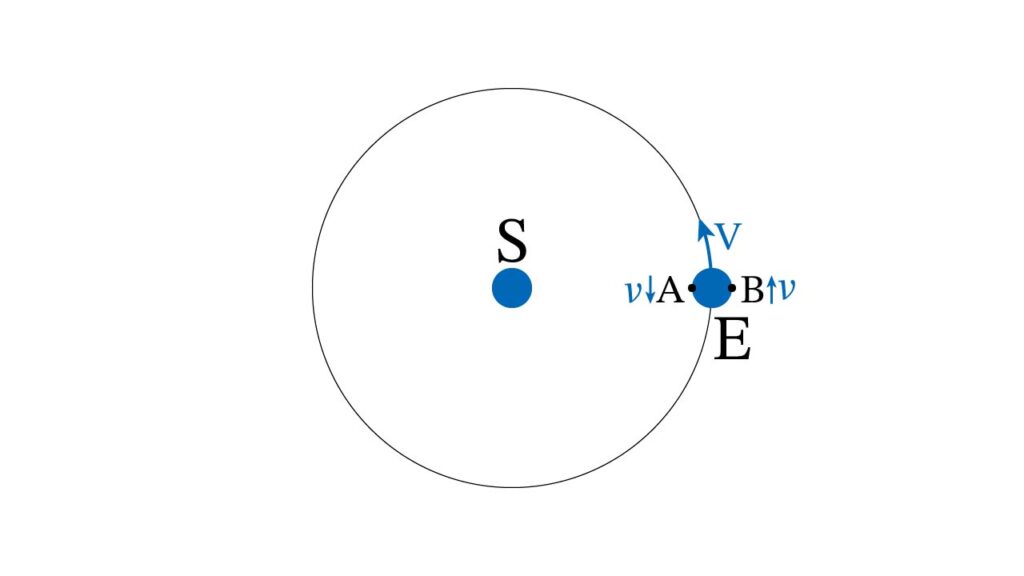
この説は天文学者だけでなく、漁師や一般の人にも誤りがすぐに分かりました。ガリレオの説では満潮は正午に起き、干潮は真夜中に起きることになりますが、干満はいつでも生じます。また、この説では干満の周期は12時間となりますが、実際の周期は6時間です。漁師たちは誰でも干満が月の運行と関係があることを知っていました。満潮は月が出ているときとその地球の裏側で、時間が少し遅れて生じ、干潮はその中間の時間に生じます。しかし、この説自体はガリレオでなければ思いもつかない斬新で独創的な説です。

慣性の法則

ガリレオは著書の中で力学における重要な事実も述べています。それは“慣性の法則”と呼ばれるものです。「速く走る船のマストの頂上から石を落とした場合、船がどれほど速く走っていようとも石はマストの根元に落ちる」というものです。一般には慣性の法則はニュートンが発見したことになっていますが、最近では「ガリレオ・ニュートンの慣性の法則」と呼ぶ人もいます。

この説は「地球自転説」の中で述べられたもので、「もし地球が自転しているとすれば、激しい東風が吹きすさび、空を飛ぶ鳥は西に流され、大砲の弾の飛距離も方向によって違いが出るだけでなく、すべてのものが西に吹き飛ばされる」という旧来の“地球不動説”への反論です。 しかし、このときはもう100年以上も前にコロンブスがアメリカ大陸まで出かけており、地球は球で宇宙に浮かんでおり、自転していることは航海士や天文学者なら誰でも知っていることでした。もちろん一般の人の中には、「地球は平坦で境があり、境では滔々と海の水が流れ落ちている」とか、「月の向こう側は天上界で地上界とは別の世界が存在している」と信じる人がいっぱいいました。ガリレオの著作は、学問的に正確に書かれてはいますが、3人の登場人物の会話で構成された文学書でもあったのです。ですから、「地球が公転しているかどうかの問題に、すでに解決済みの自転を引き出すのは問題のすり替えだ」という意見は通りません。当時は学会とか専門の学術誌などなかったので反論する術(すべ)はありませんでした。

『天文対話』では、地動説（太陽中心説）を擁護する議論が続きますが、その主眼である潮汐現象は誤りだったのです。これ以外に地動説を支持する明確な根拠はなにも書かれていません。当時の天文学者にはプトレマイオス説（天動説）を離れられない理由がありました。それは四季（春分夏至秋分冬至）の4つの期間の長さがそれぞれ異なるからです。ローマキリスト教はカレンダーの制作に責任を持っていましたから、正確な予測ができるプトレマイオス説から離れられなかったのです。

この時代の暦に関する詳しい記事はこちら▼
『Web連載 暦の起源』中世ヨーロッパの暦

ガリレオの公準 – 速度に関する誤った原則

長さや時間の扱い

さて、「落下の理論」に参りましょう。ガリレオは“数”についてどのように考えていたのでしょうか。ギリシアの幾何学では、数といえば自然数だけで、長さなどは“量”として“数”とは別ものとして扱われていました。ガリレオは、長さや時間などの量を自然数で表していますから、量と数の境界があいまいになってきており、そろそろ“実数”という用語を用いてもよい時期に来ています。しかしガリレオにとって依然として“数”とは自然数だけです。つまり、自然数 a に対しては、平方 a² とか、平方根(の近似)  は計算できますが、a が長さの場合はまったく別の方法がとられました。これらについては次節で解説します。

落下の実験

以下では落下とは、自由落下のことで、空気などの抵抗のない場所で、初速度 0 からの落下のことを意味します。また、坂の上から転がり落ちることも落下とします。以下では、ガリレオが“速度”をどのように考えていったかを考えます。

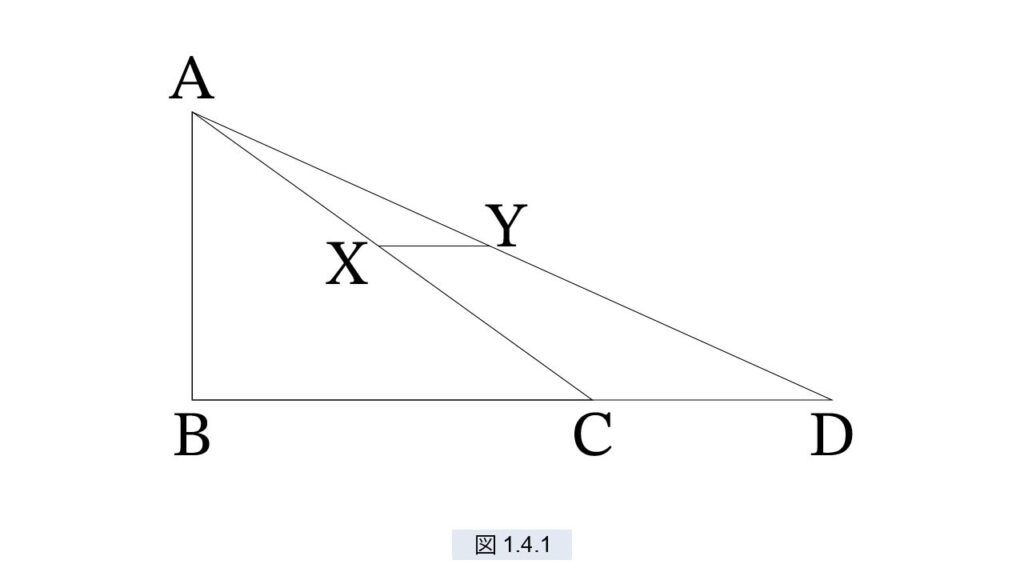
図1.4.1 で、A から坂AC と AD に球を落とします。X は AC上の点、Y は AD上の点で、XY は CD と平行とします。X における速度を v(X)、Y における速度を v(Y) とします。したがって v(A)＝0 です。ガリレオは次を公準としました。

すなわち次が成立します。

v(X) ＝ v(Y)

公準ですから、ガリレオはこれを証明していませんが、現在の理論からこの公準は正しいことが証明されます。ガリレオはこの公準を使って「落下の理論」を構築しようとしましたが、すぐに「誤った原則」という“迷宮”に陥ってしまいました。皆さんはどこが誤りか指摘できますか。

これを式で表すと次のようになります。図1.4.1 参照。

v(X) : v(C) ＝ AX : AC,
v(Y) : v(D) ＝ AY : AD

ガリレオの時代、まだ“速度”という概念はありません。理論を作り上げるときにはいろいろな仮説を立て、それが失敗に終わることなど普通のことです。ガリレオが「落下の理論」を完成するのは著作『新科学論議』(1638)であって、それまでは手稿とか手紙類にある資料であり、途中経過に過ぎません。

ガリレオが考えた瞬間速度と全体速度

ガリレオが「公準」としたのは、速度をこのように定義すれば、多くの定理がこの公準から導かれると予想したのでしょう。実際ガリレオの残した資料には 図1.4.1 と類似の 図1.4.2 が描かれています。

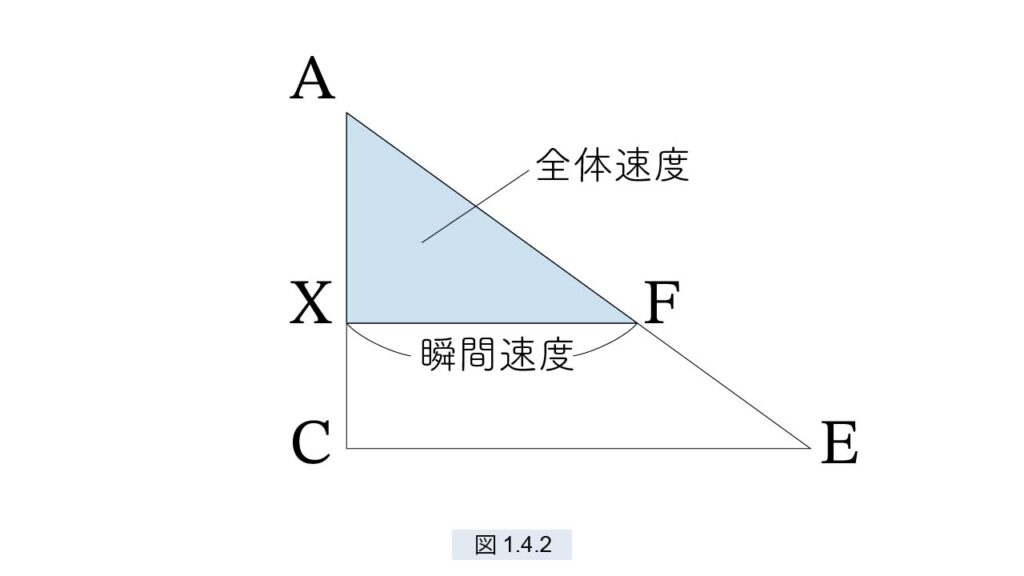
図1.4.1 で、A から C へ球を落下させます。ガリレオは 図1.4.2で、X における“瞬間速度”と“全体速度”という2つの速度を定義しています。

線分 XF は点 X における瞬間速度である。線分 AC には無数の点があり、すべての点 X で瞬間速度が定義される。点X における全体速度とは、AX 上のすべての点の瞬間速度の総和、すなわち三角形 AXF の面積である。△AXF と △ACE は相似であり、相似の三角形の面積は辺の平方に比例するから、

全体速度は落下した距離の平方に比例する

ガリレオの“瞬間速度”も“全体速度”も現在の速度から見ると誤りです。正しいのは

速度は落下した距離の平方根に比例する

です。しかしガリレオは長い間これに気がつきませんでした。これまでギリシアの幾何学で扱われてきた量は、長さ、面積、体積、角度だけです。速度とか時間を新たな量として導入し、その上で理論を構築したのはガリレオが最初です。速度や時間を線分（の長さ）として表すことは、画期的なことだったのです。更に当時は比例といえば、「～は…に比例する」と「～は…の平方に比例する」だけで、「～は…の平方根に比例する」は思いもよらなかったのです。「平方に比例する」と「平方根に比例する」とは言葉は似ていますが、逆の概念です。

図1.4.3 は正しい速度と距離の関係を表すグラフです。図1.4.2 と比べてください。AX＝s, XF＝v とおくと、このグラフは

v = a √s　　　（速度は距離の平方根に比例）

を表しています。

前節の〔 高台と坂の実験 〕では、平方根 √s を計算しました。しかしこれは s が自然数のときに限ります。ガリレオは小数を知りません。「長さ s の平方根に対する比」に関しては、代数的な計算ではなく幾何学的な作図による方法によるしかなかったのです。ガリレオがこれをどのように扱ったかを見るには、当時の比の理論を知る必要があります。次節では「比の理論」について解説します。

【参考文献】ガリレオの迷宮　　高橋健一著、共立出版 (2006)