落下の実験

ガリレオ・ガリレイは近代科学の生みの親とも呼ばれ、天体観測により数々の驚くべき発見をしました。ガリレオが残した天文学に関する業績については、彼の伝記の中で数多く語られています。しかし、ガリレオが数学において後世に与えた絶大な影響を詳しく述べているものはあまり多くありません。本連載では当時の時代背景を踏まえ、ガリレオの残した業績を詳しく調べていきます。今回はガリレオが行った「落下の実験」について、彼の著作や資料の記述を元に考察します。

ガリレオ・ガリレイの数学 第一話はこちらから▼
〔ガリレオ・ガリレイの数学 1.科学の時代の始まり〕

落下実験に関する逸話

ピサの斜塔の実験

ガリレオは「落下の理論」を作り上げました。この理論に関する実験として「ピサの斜塔から大小2つの球を落下させて、物体の落下速度は物体の重さに関わらず一定であることを証明した」という話は有名です。

しかし、ガリレオがピサの斜塔から物を落として落下の実験をしたというのは、どうやら伝記作家の作り話のようで、重い物体と軽い物体がほぼ同時に落下するという事実は当時すでに知られていたようです。

落下実験の道具

ガリレオが落下の実験に用いたといわれる道具が、フィレンツェ科学博物館に展示してあります。物を垂直に落とすとスピードが速すぎて時間が計測できないので、坂を作り坂の上から金属球を転がすというもので、博物館にあるものは18世紀末に講義で使われたもののようです。（以下はイメージ図）

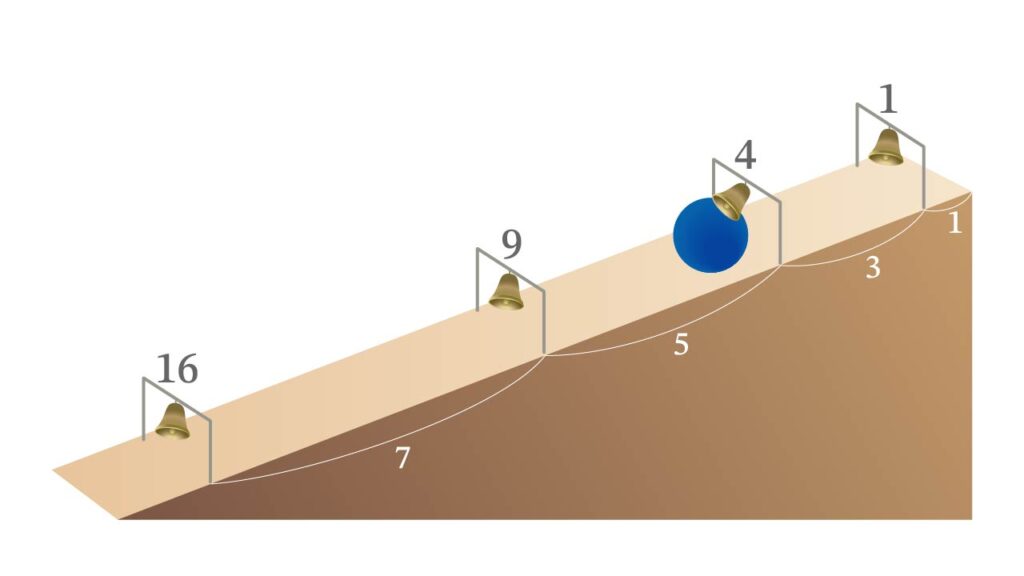
坂の斜面に、上から距離1、距離4、距離9、距離16の位置に鈴が取り付けられていて、球が通ると鈴がなるようになっています。また、球を坂の上から落とすと同時に振り子を動かします。すると、振り子の振りに合わせて鈴が鳴り、ガリレオの落下の法則が正しいことを示します。 鈴と鈴の位置の差は、(一番上を位置0とすると) 1, 3, 5, 7 と奇数列となっています。奇数列の級数（すなわち部分和の列）が平方数の列

1, 1+3＝4, 1+3+5＝9, 1+3+5+7＝ 16, …

となっていることは古代ギリシアの数論でよく知られていました。つまり、球が通過する距離は時間の平方数となっています。ガリレオが発見したこの事実は「時間平方則」と呼ばれています。

ガリレオの実際に行った実験方法

著書『新科学論議』の記述

ガリレオはこの方法で実際に実験したのでしょうか。20世紀に入ると多くの科学史家たち（たとえばパリ高等研究所のアレクサンドル・コイレ1953年など）が、この実験に懐疑的な意見を述べ始めます。実験を信じない理由は、ガリレオが時間の計測に使った方法です。

ガリレオの著作にはどのように記されているのかを見てみましょう。『新科学論議』には次のように書かれています。方法は上で述べた博物館にあるのとほぼ同様ですが、坂には一定の距離ごとに印は付けられていません。最初は、球を一定の距離転がし時間を測ります。時間は脈拍で測りました。もちろん誤差が生じますから、この行為を何回も繰り返します。それがすむと、同じ球を距離を 1/4 にして時間を測ります。その降下時間を測ると、先ほどの実験の半分であることが分かりました。坂の傾きや、距離の比をいろいろ変えて、実験をたっぷり 100回繰り返し、常に通過距離は時間の平方に比例することが判明しました。

時間の測定方法 – 水時計による測定

また、時間の測定方法も、次のような方法に変えました。大きな桶を高いところから吊り下げておき、球が坂を通過する時間だけ水が細い管から小さな器に受けるようにしたのです。その水の量を極めて正確な天秤で計り、その重さの比から時間の差を得ました。

後に書かれた伝記には、この水時計についてのさらに詳しい記述があります。まず、距離はプントという単位で測りました。

1プント ＝ 0.094 cm ≒ 1 mm

水の重さはグレインで測りました。

1オンス＝480グレイン、1グレイン≒ 0.065g

ガリレオは、16グレインの水が流れ出す時間を「テンポ」と名付けました。これは92分の1秒に相当します。長さにしても、重さにしても、時間にしても、とても小さな単位です。当時、これだけの精度で計測できたというわけではなく、（後で述べる）平方根の計算などで大きな自然数が必要だったのです。ガリレオは、単位として十分小さいものを採用すれば、実用上問題ないと考えていたようです。

ガリレオはこの実験で「時間平方則」の発見したのか

多くの人がこの実験が可能かどうかの追試を行っています。たとえばコーネル大学のトマス・セトルは、1961年にサイエンス誌に論文を投稿し、「装置に十分熟達すれば実験は可能だ」と発表していますし、日本のテレビでもガリレオの実験を再現しています。

博物館の展示物が示すガリレオの実験は、すべての見学者を驚かし、納得させるものです。しかし、科学史家が疑問に思っていたのは、果たしてこの方法でガリレオが「時間平方則」を発見したのか、という疑問です。頭脳だけでの「思考実験」でこの法則を導き出し、実際の実験は結果が正しいことを示すだけのデモ用の「追試実験」だったかもしれない、という疑いです。

資料 〔手稿107v 〕に記された実験結果

実際にガリレオが行った実験はこれとは異なることを裏づけるデータが残っています。それはフィレンツェ国立中央図書館蔵の手稿107v と呼ばれる資料で、『迷宮』によると次のような装置を使った実験です。角度 1.7度、長さ約 2m の坂を用意します。上で述べた博物館の装置や『新科学論議』に記された方法では、距離を設定しておいて時間を計測しましたが、手稿 107v では、時間を設定しておいて距離を測定します。球が通ると音が鳴る仕掛けを坂にセットし、坂の上から球を転がし、音と音の間隔が一定になるように調整します。おそらくガリレオは旋律の速い歌いながら、1拍子＝約1秒となるように調整したのでしょう。

つまり、ガリレオは時間を計測したのではないのです。1秒ごとに球の通過する位置に印をつけておき、印と印の間の距離を計測したのです。次のような実験結果が残っています（手稿107v  フィレンツェ国立中央図書館蔵）。

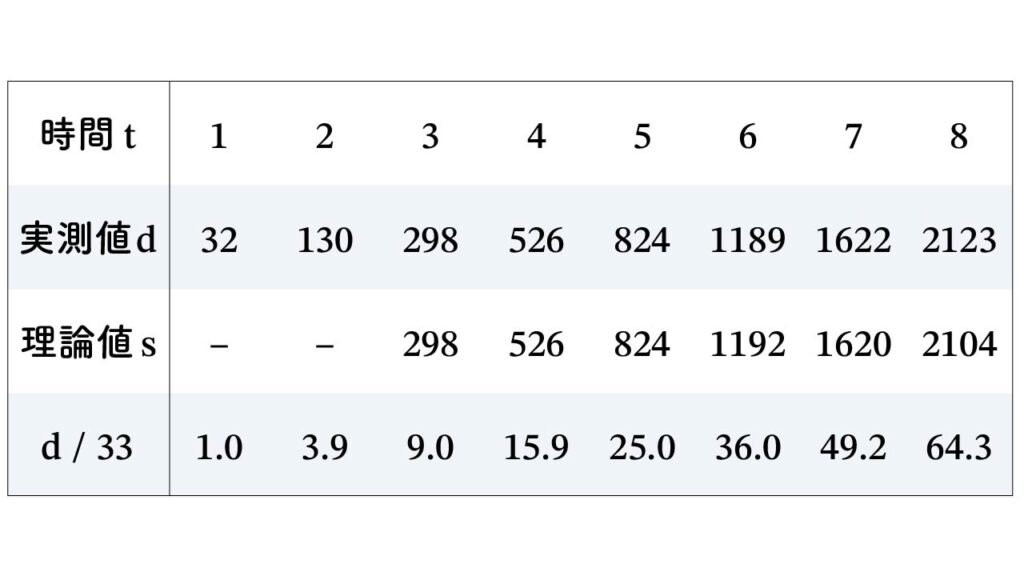
理論値 s は、ガリレオの考えた理論値です。t＝ 1～5 については理論値と実測値が同じですから、t＝6 と t＝8 について、ガリレオがどのように理論値を計算したか見てみましょう。「時間平方則」は、時間が倍になれば距離が4倍となることを意味します。したがって、t＝6 のときの理論値は、t＝3 のときの4倍、298×4＝1192 で、同様に t＝8 のときは t＝4 のときの4倍、526×4＝2104 で計算します。t＝7 のときの理論値をガリレオがどのように計算したかは不明です。

現在なら、公式 s ＝ at² を使って、実測値と理論値を比較します。a＝33 として、d/33 を計算してみました。現在の式ですから小数を使いましたが、四捨五入すると

1, 4. 9, 16, 36, 49, 64

ときれいに平方数の列となります。

『新科学論議』に関する考察

この実験をガリレオが行ったのは1604年ごろのようです。一方『新科学論議』が出版されたのが1638年で、時間的にずいぶん開きがあります。ガリレオは「時間平方則」に自信を持っており、ふたたび同じ実験をしたとは思えません。

『新科学論議』は、3人の登場人物の会話で成立する物語で、ガリレオは物語作家としても非常に有能であり、実験方法のこまかな描写などから本当にこの実験が行われたように描かれています。しかし、実験データの記述はなく、またこの時期に同じ実験を繰り返す必要などなかったはずです。ですから、時間を脈拍で測ったとか、水時計を作ったという話はガリレオ特有の作り話の可能性があります。ではなぜ実験の方法を『新科学論議』で変更してしまったのでしょうか。この理由については、後の節で考えることにしましょう。

時間平方則

誤った原則による証明

ガリレオの「時間平方則」は、歴史に残る発見といえますが、この事実が物理とか数学の発展に与えた影響はあまりなさそうです。ガリレオの功績は何といっても「数学の創造」ですが、ガリレオはこの時点ではまだ「落下の理論」はまだ完成していません。というのはガリレオはこの事実を「誤った原則」から証明してしまっているからです。「誤った原則」とは

「速度は距離に比例して増加する」

という原則です。このことは、ガリレオがヴェネチアの有名な神父で神学者のパオロ・サルピに宛てた手紙（1604年）が残っていて、その中でガリレオは「自由落下において、速度は移動した距離に比例する」こと、および「時間平方則」が成立することを述べています。（自由落下とは、抵抗などがない環境での、初速度 0 からの落下を意味します。）

ガリレオの先進性

ガリレオの初期の記述には誤りがいくつかあり、この「時間平方則」の証明は間違っています。しかし、手紙とか手稿は正式な論文とか著作ではありません。さらにガリレオは当時まだ、“速度とは何か”という明確な考えを持っていなかったのです。したがってとりあえず「速度とは距離に比例するもの」という仮説を立てて議論を進めることは間違いではありません。

ガリレオは、距離が増加すれば速度も増加する根拠として、物を高いところから落とした場合と低いところから落とした場合の地面に与える衝撃度が異なることを挙げています。このことは後の“運動量”に結びつく考え方で、ガリレオの先進性を示しています。

時間の概念

現在の速度の定義を知っている人は、「なぜガリレオは“時間”を基準に考えなかったのだろう」と思うかも知れません。本シリーズの〔暦の起源 第12回 中世ヨーロッパの暦〕で述べたように、当時のヨーロッパでは、カレンダーでさえ日にちは数字ではなく聖人の名前でした。時間は教会の鐘の音で知るだけで、自分の年齢も知らない人が多かったようです。

もちろん時間を測る正確な時計などありません（脱進器の付いた振り子時計は1659年にホイヘンスが発明）。ガリレオは天文学者でしたから、「絶対的時間が存在する」ということは知っていましたが、正確な計測方法は知りませんでした。幾何学で扱うのは線分です。当時ガリレオが扱える“計測できる量”としては長さしかなかったのです。したがってまず長さを基準としたのでしょう。

『迷宮』の著者は、「ガリレオは、誤った原則に囚われ以降20年以上の長きにわたり迷宮をさ迷い歩くことになる」と述べています。ガリレオのすごいところは、この問題を20年以上も考え続けたことです。ガリレオはこの実験以外にもさまざまな実験をしています。次節でその実験を見てみましょう。