再帰構造 とは

相似な図形をその中に含む構造をもつ図形のこと。

（例）2辺の比が黄金比 a : b となる黄金長方形
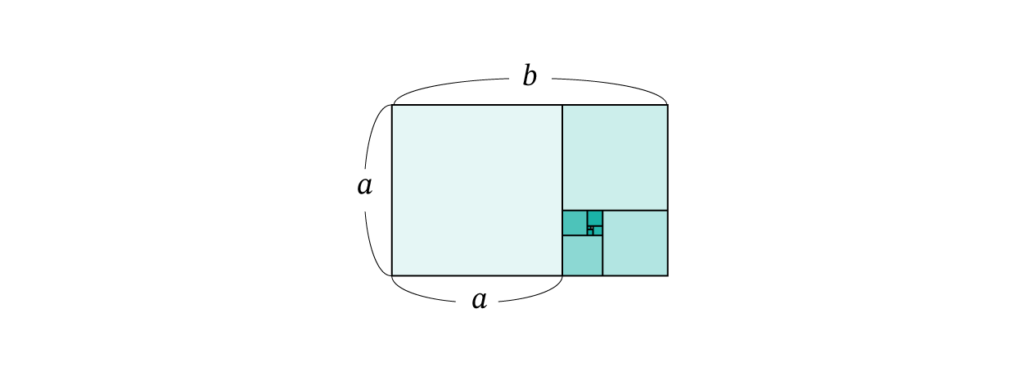
黄金長方形から、a × a の正方形を切り取ります。すると残りの部分も黄金比の長方形になります。さらに、残りの長方形に対しても、正方形を切り取るという操作を適用することができ、無限に続く再帰構造になります。

Mathematicaでは電子書籍を販売しています

ポゥじいとめぐる『数』の旅 シリーズ

ポゥじいとめぐる『数』の旅シリーズは、数学史を対話形式でわかりやすく解説した電子書籍です。中高生の学びから、大人の知的好奇心まで幅広く応える入門書。数の歴史や発見の物語を、やさしく楽しくお届けします。

詳しくはこちら