
等加速度運動
ページ目次
等速運動と等加速度運動
等速運動
ガリレオは一様に速度が増加していく“等加速”という概念に到達しましたが、まだ速度の増加する割合を示す “加速度” という概念には至っていません。これはガリレオの後を継いだニュートンの業績ということになっていますが、ガリレオ自身も2つの等加速度運動の速度(の増加率)の違いについて議論しています。
等加速度運動の議論の前に、前節で述べた 等速運動 の復習をしましょう。現在の皆さんは速度が「速度=距離/時間」と定義されることを知っていますね。このように理解して以下を読んでください。
2つの等速運動する物体 A と B があります。A は速度 v1 で t1 時間かかって距離 s1 進み、B は速度 v2 で t2 時間かかって距離 s2 進むとします。
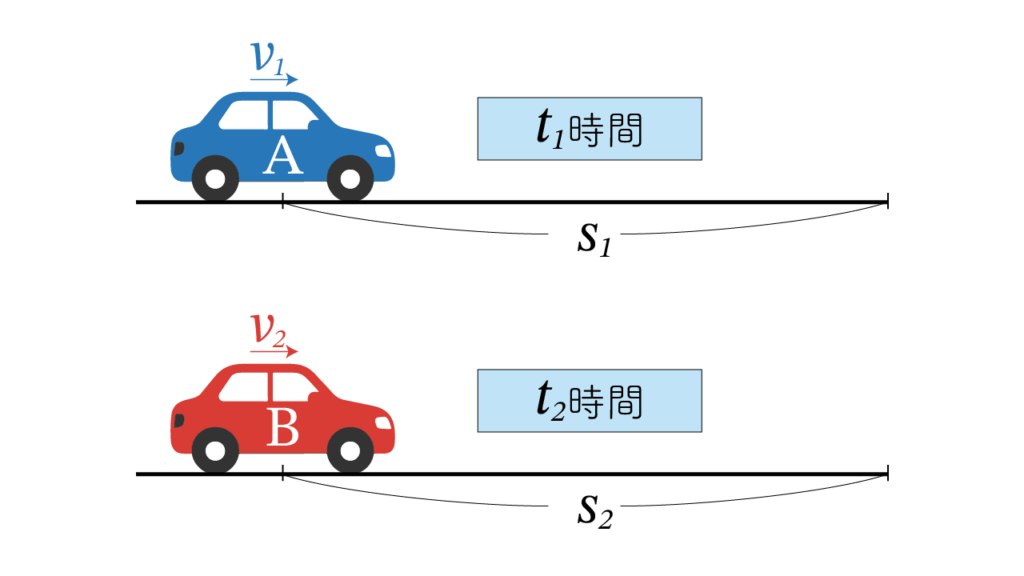
次の (i) は等速運動の定義、(ii) は等速運動の定理です。
(i) 時間が等しいなら距離は速度に比例する。 t1 = t2 ⇒ s1 : s2 = v1 : v2
(ii) 速度が等しいなら距離は時間に比例する。 v1 = v2 ⇒ s1 : s2 = t1 : t2
現在の皆さんは (i) と (ii) が公式「速度(v) = 距離(s)÷時間(t)」から得られることが分かると思います。( (ii) が定理となっているのは、ガリレオが以下で述べるように速度をギリシアの幾何学を使って定義しているからです。)
ガリレオは、距離、時間、速度の関係が、「比例論」の基本概念である長方形の、面積、底辺、高さと同じ振る舞いをすることに気がつきました(ギリシアの幾何学では、長方形ではなく平行四辺形ですが本シリーズでは長方形に制限しています)。2つの長方形 A と B があります。A の底辺は a1、高さは b1、面積はs1 とし、B の底辺は a2、高さは b2、面積はs2 とします( 図1.7.1 )。
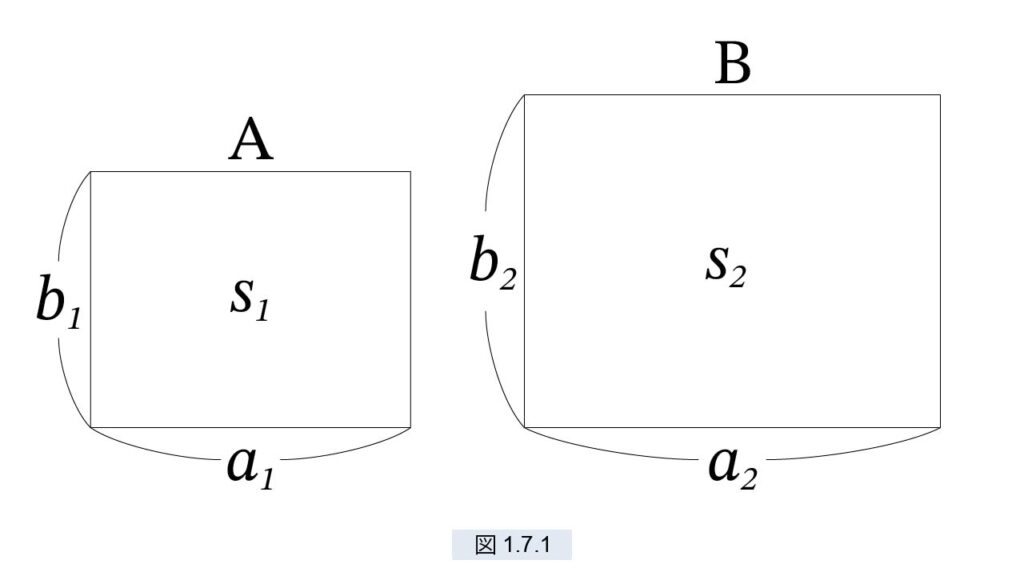
このとき次が成立します。
(i) 底辺が等しいなら面積は高さに比例する。 a1 = a2 ⇒ s1 : s2 = b1 : b2
(ii) 高さが等しいなら面積は底辺に比例する。 b1 = b2 ⇒ s1 : s2 = a1 : a2
すでにガリレオは、時間や速度を線分(の長さ)で表していました。そこでガリレオは
距離 = □(時間, 速度)
と考えることにしました。つまり、「距離とは、底辺が時間で、高さが速度の長方形である」としたのです。距離と時間はすでに分かっています。速度とはこの式を満たす高さを表す線分のこと、と考えることにしたのです。面積は、数値とか線分とは関係のない抽象的な量です。
等加速度運動
等加速度運動 にまいりましょう。落下 AC を考えます。AC は坂でも鉛直でもかまいません。
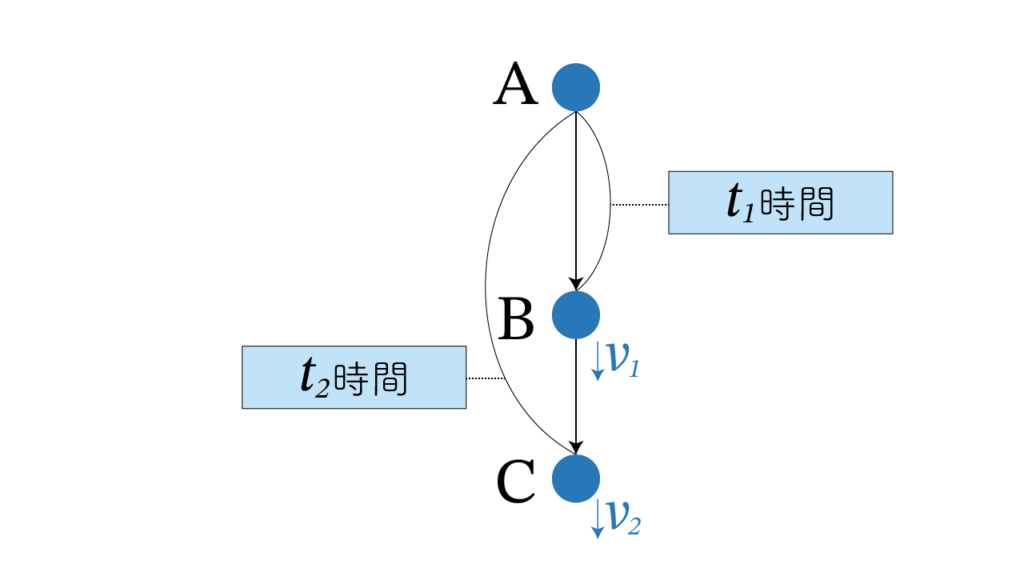
点 B を AC 上の任意の点とし、
AB に要する時間 t1, AC に要する時間 t2
B での速度 v1, C での速度 v2,
と置きます。等加速度運動とは
v1 : v2 = t1 : t2 (1)
が成立する運動のことです。つまり、時間(t)に比例して速度(v)が増加する運動です。ガリレオは 図1.7.2 のような図を描いています。
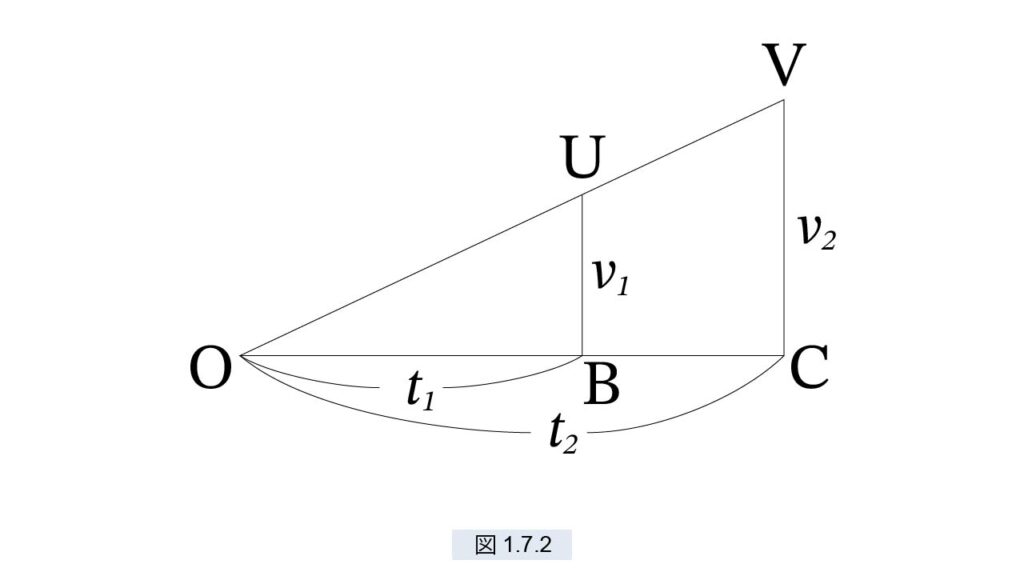
OB=t1, OC=t2, UB=v1, VC=v2
と置きます。すると、式 (1) より、△UOB と △VOC は相似になります。Bは OC 上の任意の点、UB は VC と平行な線分です。
ガリレオの公準と倍距離則
ガリレオの公準
ここで〔ガリレオの公準〕について考えてみましょう。図1.7.3 の三角形 ABC を考えます。
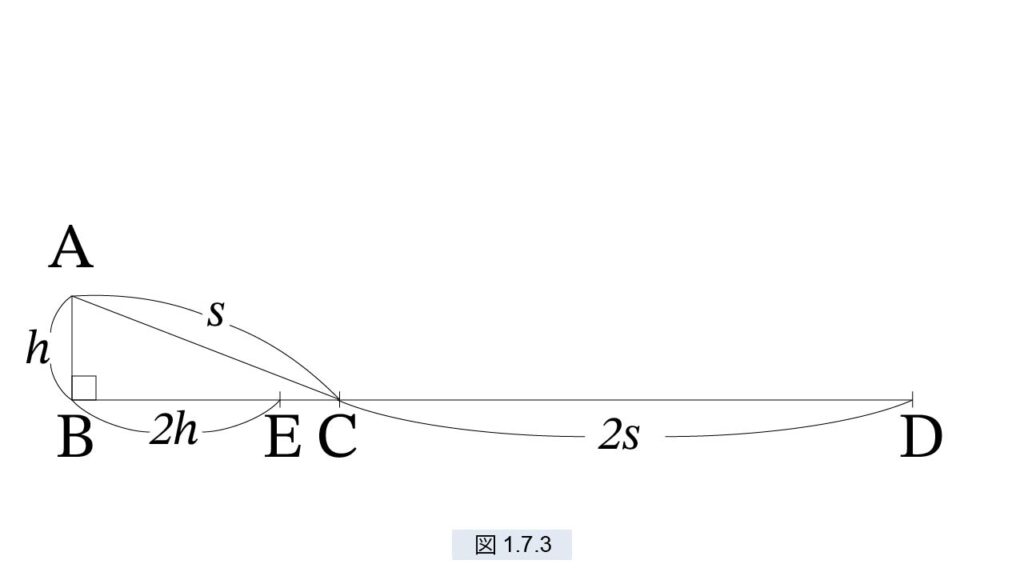
ガリレオは、A から球を転がしたとき、C での速度は坂の傾斜にかかわらず常に一定であることを発見しました。C をどんどん B に近づけます。C が B と一致すると球は A から B への鉛直落下となりますが、このときも速度は同じだと考えました。〔倍距離則〕も同様に、鉛直落下についても成立すると考えました。Aから球を落下したとき、B での速度と C での速度は同じで v とします。また
AB=h, BE=2h, AC=s, CD=2s
AB の落下時間 t1, AC の落下時間 t2
とします。すると、BE間と CD間は等速度だから
2h = □(t1, v), 2s = □(t2, v)
が成立します。高さが等しい長方形の面積は底辺に比例しますから、次が成立します。現代の皆さんは公式「移動距離=時間×速度」を使えば簡単に証明できます。
h : s = □(t1, v) : □(t2, v) = t1 : t2 (2)
これを次の定理としてまとめます。この定理は将来もっと洗練された形でニュートンによって示されますから特別な名前は付けず、定理1 としておきます。
定理 1
図1.7.3で次が成立する。ここで time(AB) はAB の落下時間、time(AC)はAC の落下時間とする。
time(AB) : time(AC) = AB : AC
定理1 は式 (2) の「t1 と t2 を time(AB) と time(AC) に置き換え、h と s を AB と AC で置き換えたもの」に過ぎません。次の定理では、定理1は式 (2) のことです。
弦の規則
ガリレオは、次の有名な〔弦の規則〕と呼ばれる次の定理を証明しています。
定理〔弦の規則〕
図1.7.4-1 のような円がある。Pは円周の真上、A は任意の点、C は真下。
P からC に達する時間とA から C に達する時間は等しい。
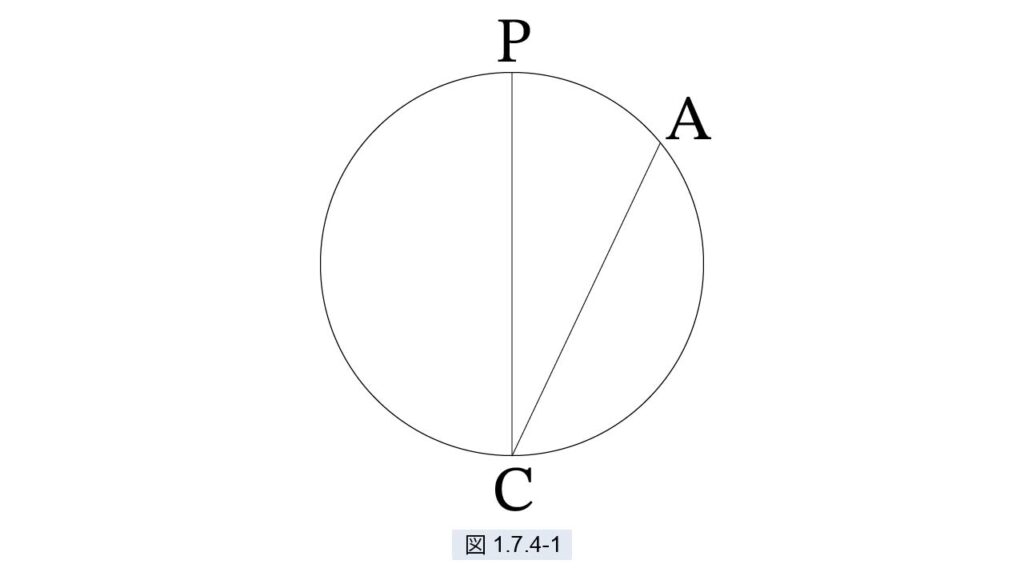
「Pから落下した球が C に達する時間と、円周上の任意の点 A から坂 AC を転がる球が C に達する時間が等しい」ということです。数学が発達した現代では、この問題を解くこと自体はそれほど困難ではないかもしれません。しかし、速度や時間といった数学的概念が何もない時代に、このような事実を発見し、諸概念を創造したことは、驚異的なことに思われます。イノベーションは、問題を解くことよりはるかに難しいのです。
弦の規則の証明
図1.7.4-2 のように長方形 AHCB を描きます。
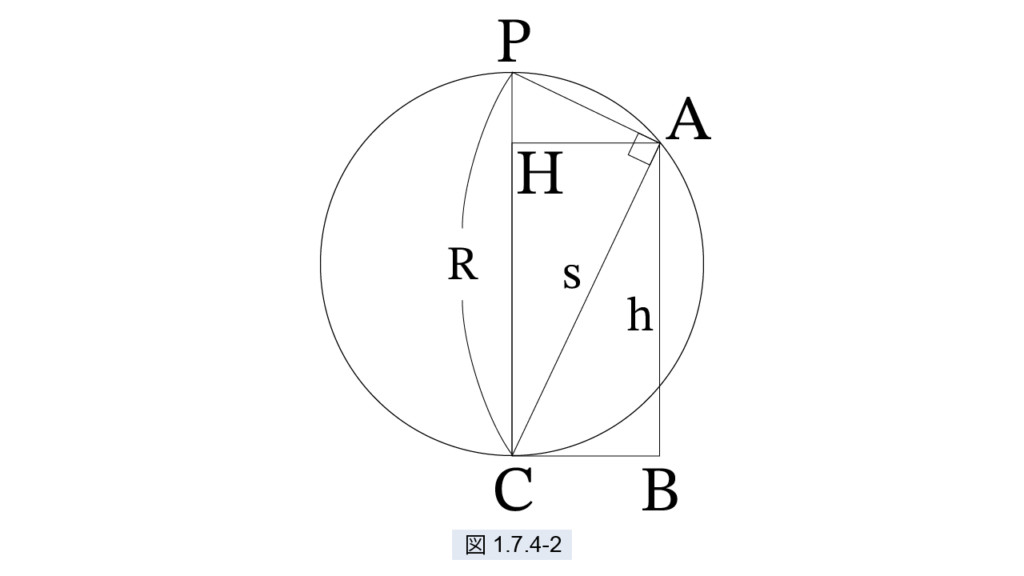
PC=R, AC=s, AB=h
time(AB)=t1, time(AC)=t2, time(PC)=t3
と置きます。AB と PC は共に鉛直落下ですから、時間平方則より
h : R = t12 : t32
が成立します。直角三角形 HCA と ACP は相似ですから
HC : AC = AC : PC すなわち h : s = s : R
が成立します。したがって、s は h と R の比例中項です。よって、
t12 : t32 = h : R = h2 : hR = h2 : s2
となり、
t1 : t3 = h : s
となります。上で述べた式 (2) より
t1 : t2 = t1 : t3
が成立します。左項の一致より、 t2 = t3 が成立します。
落下運動の理論
ガリレオの描いた「距離=時間×速度」の図
現在の私たちは、速度を公式「距離=時間×速度」として理解しています。ガリレオの時代には実数も、実数と実数の掛け算もありません。ガリレオは“速度”をどのように捉えていたのでしょうか。ここで、これまで行ってきた議論を振り返ってみましょう。 ガリレオは、時間と速度をそれぞれ線分 t と線分 s で表し、「時間×速度を」t と s が作る長方形の面積 □(t,s) であらわしました。
図1.7.5 のような坂 AC を落下します。AC=s, CD=2s, time(AC)=t, Cでの速度 v とします。
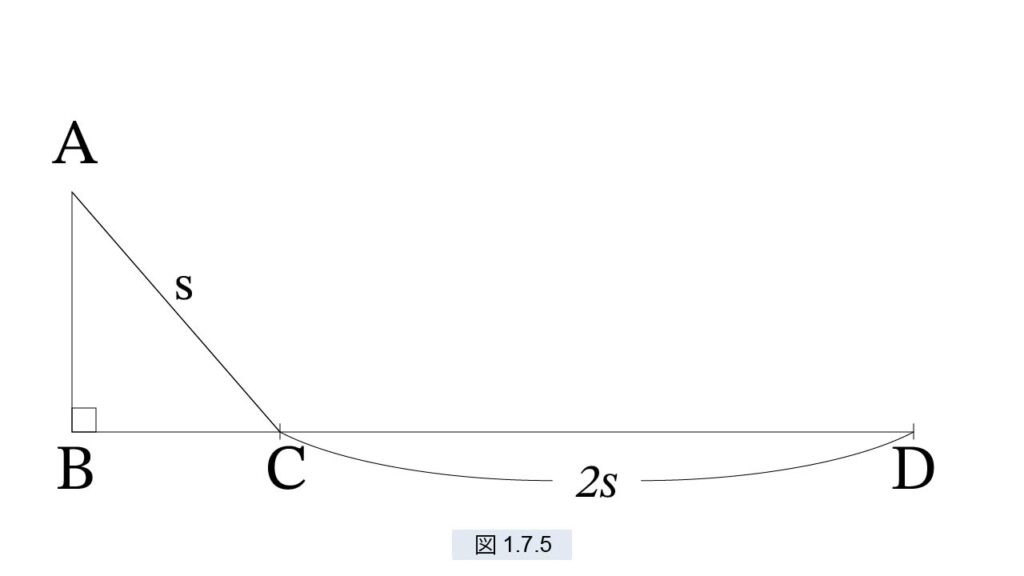
図1.7.5 は“加速度運動”を“等速運動に”変更するガリレオのアイデアです。坂 AC を転がる球は、速度 0 からしだいに速度を増し、C で速度 v となります。CD間は速度 v の等速運動です。〔倍距離則〕とは、「AC の2倍の距離 CD を、ACと同じ時間で通過する」が成立することです。
CD では速度 v、時間 t で、距離 2s を移動する等速運動だから、
2s = □(t, v)
となります。ガリレオは、坂AC の落下における速度の変化を図1.7.6のように描きました。
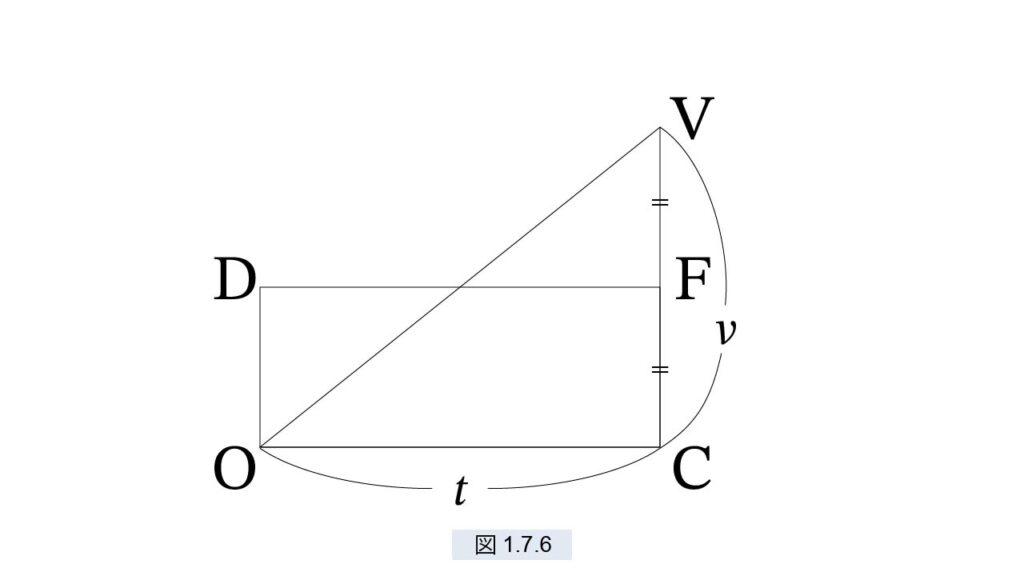
驚くことに、図1.7.6 は、現在の私たちが速度に関して描くグラフと同じです。横軸は時間軸で、縦軸は速度です。原点 O から速度 0 で出発し、時刻 t で速度 CV=v となります。この速度は瞬間速度です。ガリレオはすでに瞬間速度 の概念に達していたのです。
ガリレオはこの図で「等加速運動で移動する距離とは何か」を考察しています。CV の中点を F とします。CF は v の半分です。等加速とは、ゼロから v まで、速度が一定の割合で増加することですから、平均の速度は CF=(1/2)v です。したがって移動距離 s は
\( s = 四角形OCFD = \frac{1}{2}□ (t,v) \)
となります。ガリレオはまだ t と v は線分ですが、ガリレオの後継者たち(たとえばニュートン)は“数”と見なすようになります。明らかに
\( 四角形OCFD = \frac{1}{2}△VOC \)
ですから、ガリレオ以降、「等加速度運動」の速度の公式は
\( s = \frac{1}{2} vt \) (s:距離、v:速度、t:時間)
となります。
また図1.7.6 は、〔倍距離則〕の証明にもなっています( 図1.7.5 も参照)。坂 AC の平均速度は v の半分だから、同じ時間で進む距離は AC の倍になる。 “等加速”という概念は、「速度が時間に比例して増加する」ということで、現在なら
v = at (a は定数)
と表わせるのですが、まだガリレオはこのように表せません。ガリレオは「速度が時間に比例すること」つまり
v1 : v2 = t1 : t2
を図1.7.7 であらわしました。右の図は、AB=s1 は時間 t1 で落下する距離、AC=s2 は時間 t2 で落下する距離です。 すると次が成立します。
\( s_1 = △OBU = \frac{1}{2}□(t_1, v_1) \)、 \( s_2 = △OCV = \frac{1}{2}□(t_2, v_2) \)
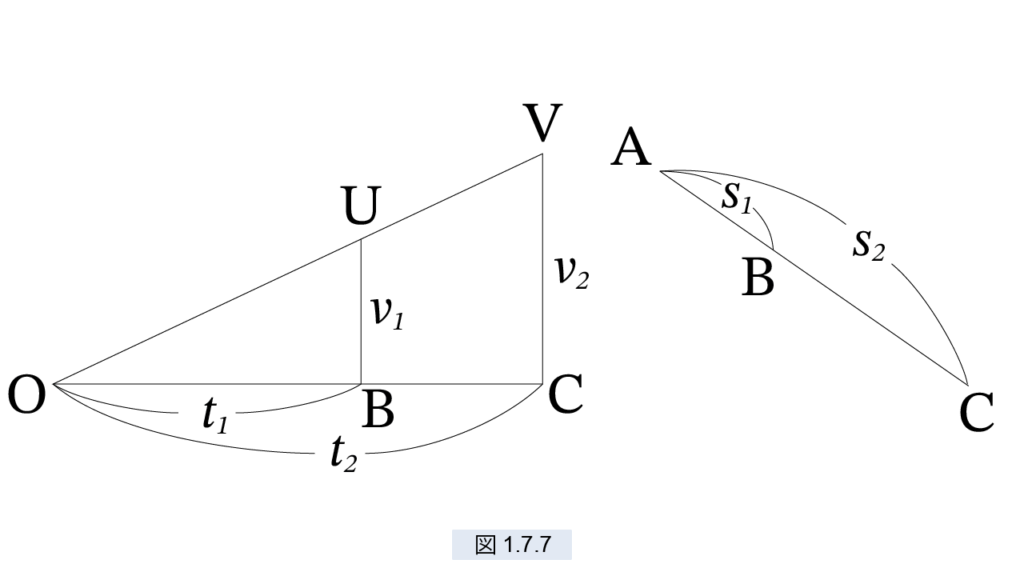
これを比で表すと、
s1 : s2 = □(t1,v1) : □(t2,v2)
となります。相似な長方形の面積は辺の2乗に比例しますから
= □2(t1) : □2(t2)
が成立します。実験で得られていた〔時間平方則〕が等加速度運動の定義から定理として証明することができました。
定理 〔時間平方則〕
等加速度運動において、移動距離は時間の平方に比例する。
ガリレオは時間や速度を「数」として扱った
ガリレオ以前、時間と速度を数学的対象とした人はいませんでした。ガリレオはこれを幾何学における線分(の長さ)として扱いました。『原論』における、長さ、面積、体積は抽象的な“量”であって定義はなにもありません(『原論』には、「点とは部分を持たないものである」とか「線分とは幅のない長さである」といった定義がありますが、これは現代数学における定義とは違います)。 ガリレオも単に、速度を等加速度運動の定義を満たす量として扱っています。 しかし、ガリレオにおける大きな進歩は、時間や速度を“数”としても扱っていることです。ガリレオにとって数とは自然数だけでしたが、単位を非常に小さいものにとれば、実用的には十分意味を持ちます。
ガリレオは、「速度は距離に比例するのではなく、時間に比例する」という事実に気がつくと「落下の理論」が急速に進みました。しかしこれは「落下の理論」だけにとどまらず、数学や物理学、いや科学全般に影響を及ぼすことになるのです。そのようすを次節で見てみましょう。
