ガリレオの実験 – 大砲の水平発射・振り子の実験

ガリレオはどうして「落下の法則」を思いついたのでしょうか。どんな研究も最初は何らかの動機があったはずです。ガリレオが落下の法則に辿り着くまでに行った数々の実験について詳しく見てみましょう。

大砲の発射実験

大砲の発射角度に関する問題

ガリレオは20代の後半にパドヴァ大学に着任します。この就職には、ヴェネチア共和国の文化サークルに絶大な影響力を持っていたジョヴァンニ・ヴィンチェンツォ・ピネルやトスカナ大公国の要塞監督官であったグィドバルド・デル・モンテ侯などの後押しがありました、着任するとすぐに、有力者のデル・モンテから町をいかにして守るか、要塞をどのように構築するか、敵の防御を打ち破ってどのように攻撃するかなどについていろいろ相談を受けました。いくつかの質問に答え、多くの提案をしました。その中で彼がとくに興味を引いたのが「大砲の命中精度を上げるために、大砲の角度はどのように定めたらよいか」という問題でした。当時の考えでは、大砲の弾は直線を描いて飛び、やがて勢いを失うと地面に落ちてくるというものでした。当時の図が残っていますが、まだ放物線らしく書かれていません。

 

ガリレオは実験を繰り返します。発射する角度はどんな角度でも、中央で最高度に達し、発射した角度と同じ角度で着弾します。45度の時飛距離は最長になります。発射角が30度のときと、60度の時は、飛ぶ高度は異なるが同じ時点に着地することを発見します。ガリレオはいろいろな角度で実験し、ついにいくつかの事実を発見します。

軍事コンパスの製作

ガリレオはこの発見をそのままにするはずはありません。1597年に大砲用の標準器（軍事用コンパス）を製作します。大砲と火薬量ごとに砲弾の初速度が決まっていますから、角度さえ定まれば飛距離が求まります。この道具のできはよく評判も良かったので、この道具を生産する工場をみずから建て、1603年には一財産を築きました。ガリレオの行った実験を見ると、この工場で得た経験や工夫が生かされているように思われます。

1591年父が亡くなり、長男としてのガリレオは弟の学資や2人の妹の結婚資金を稼がねばならず、さらには2人の娘や息子が生まれ、家庭の負担も生じます。ガリレオは大学の給与以外にさまざまな形で収入を得ます。得意の占星術、裕福な貴族の息子の個人教授、自宅に学生を下宿させること以外に、自宅の一部を工房に改築し、職人を雇い、発明した望遠鏡や軍事用コンパスをガリレオ自身も職人と一緒になって制作しました。さらに、貴族や有力者たちに、望遠鏡やコンパスがいかに軍事用器具として役に立つかという売り込みも忘れませんでした。

大砲の水平発射

大砲の実験に関しては、1609年にアントニオ・デ・メディチという貴族に出した書簡に記されています。実験はむやみに行うのではなく、原理を見つけやすい特殊な設定で行っています。高台に置き、きっちり水平に標準を定め、火薬の量をいろいろ変えて発射します。火薬の量を変えるということは初速度を変えるということです。その結果、火薬の量に関わらず、弾丸が地面に達する時間が同じであることを発見します。さらにこの時間は、弾丸を高台から真っすぐに落として地面に達する時間と同じであることを発見します。つまり、水平方向の運動は、鉛直方向の運動（つまり落下運動）とは独立であることを発見したのです。

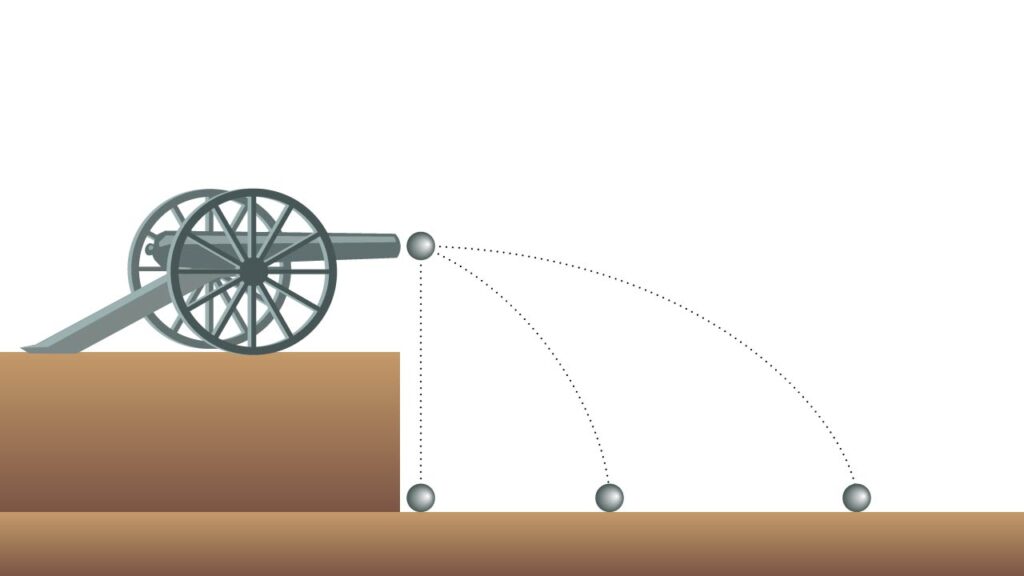
さらにガリレオは、同様のことをいろいろな角度をつけた射撃で実験しています。火薬の量を調整して、いろいろな角度で鉛直の高さが同じなるようにします。すると、どんな角度でも地面に達するまでの時間は同じとなりました。このことは、弾丸の軌跡が互いに独立な鉛直方向の運動と、水平方向の運動との合成であることを示唆しています。この実験も、後に「落下の理論」を完成させる際の重要なヒントになりました。

振り子の実験

振り子の振れ幅の観察

1602年に、パトロンの一人デル・モンテ侯宛てに書簡を送り、その中で振り子の実験に関して次のように述べています。

2本の同じ長さの細糸を用意し、それらを AB, IJ とします（図1.3.1）。それぞれの端 A と I は2本の釘に結びつけ、もう一方の端 B と J には小さな鉛玉を付けます。これらの鉛玉の重さは異なっていてもかまいません。そして、一方は弧 BC を大きく、他方は弧 JK を小さく、鉛直線 AC, IKから離します。そして両方を同じ瞬間に放ちます。すると、一方は大きな弧 BCD を描き、他方は小さな弧 JKL を描きますが、運動体 B が弧 BCD を通過する時間は、運動体 J が弧 JKL を通過する時間と等しいのです。このことを次のようにして確認しました。私が運動体 B の往復を 100回数える間に、もう一人の観察者が運動体 J の往復を 100回数えます。何度も繰り返しましたが、1回も余計になることはありませんでした。

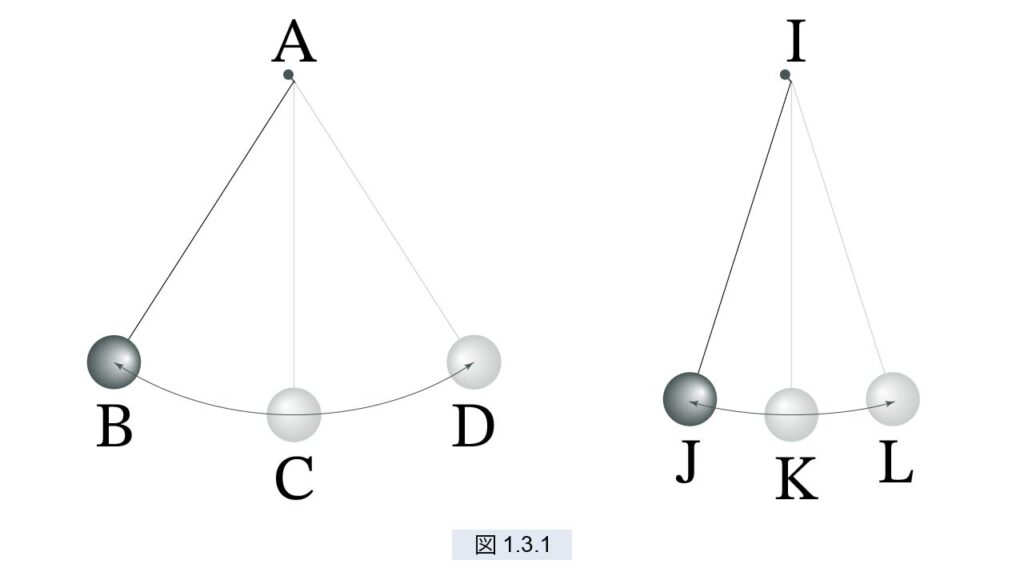
時間を脈拍で測ってはいません。また、ガリレオは実験には誤差がつきものであることをよく理解していました。100回往復を数えれば、誤差は 200分の1となります。

振り子の等時性と落下の関係

振り子の等時性と落下とはどのような関係にあるのでしょうか。ガリレオは、この振り子の実験を次のように拡張しています。この中で、ガリレオは“モメント”という概念を用いていますが、この概念はガリレオ以後、“力”とか“エネルギーの保存則”といった概念を生み出します。

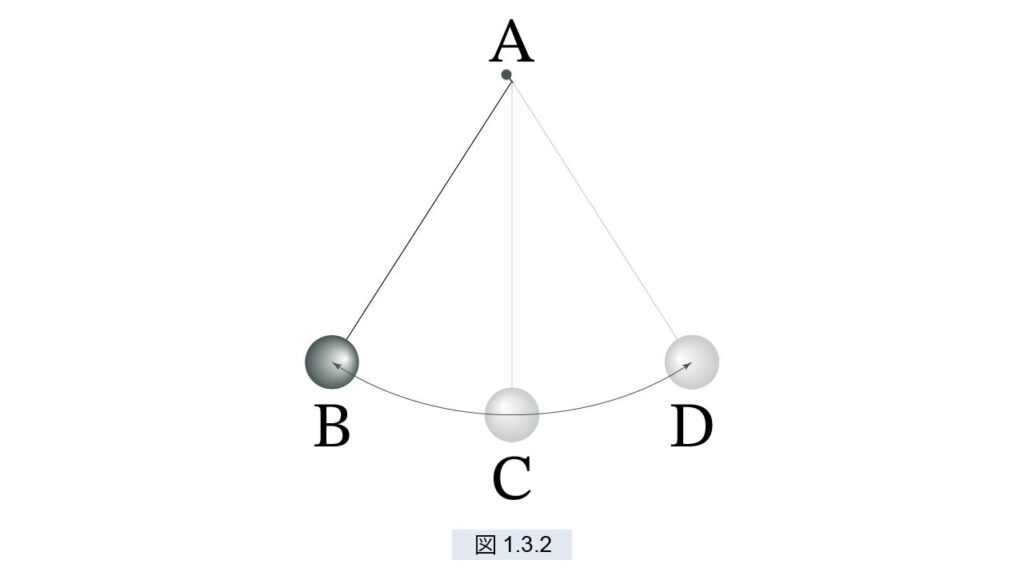
図1.3.2 のように細糸 AC に鉛玉をつけ、Aを中心として振ります。B から最下点 C を過ぎると、B と同じ高さの D に達します。D で折り返し C を過ぎて B まで戻ります。ここでガリレオは“モメント”という概念を用います。B にいる鉛玉は、下降によって C に達したとき、モメントを得る。そのモメントは、鉛玉を D まで持ち上げるのに使われます。弧DC の下降によって得られるモメントは弧BC の下降によって得られるモメントと同一です。

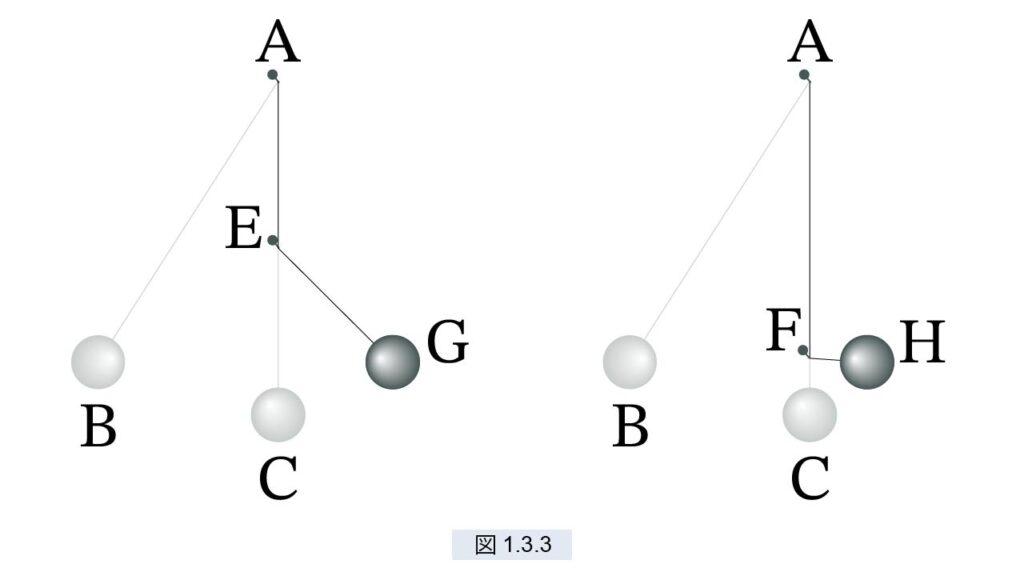
ガリレオは AC上 の点 E と F に釘を打って実験を続けます（図1.3.3）。点 E に釘を打った場合、B から C に降下した鉛玉は、釘 E に出会うと弧 BC に沿って上昇し、B と同じ高さの G に達します。その後は弧 GC に沿って下降し、B まで上昇します。釘を F に打った場合の振る舞いも同様です。釘が E にある場合、弧GC を降下する鉛玉は、EG を細糸とする振り子です。F に釘がある場合も同様です。弧DC, GC, HC に沿って運動する運動体が得るモメントはすべて等しく、B まで持ち上げます。

ガリレオは大砲の発射実験以来「速度とは何か」を考え続けました。上の振り子の実験で、モメントは落下の高さだけで決まることを発見しました。モメントは“速度”を引き起こす原因です。ガリレオは次を速度の公準としました。（「ガリレオの公準」という名称は『 ガリレオの迷宮　共立出版 (2006)』の著者の命名です。）

ガリレオの公準

斜面の高さが等しければ、落下地点での速度は等しい。

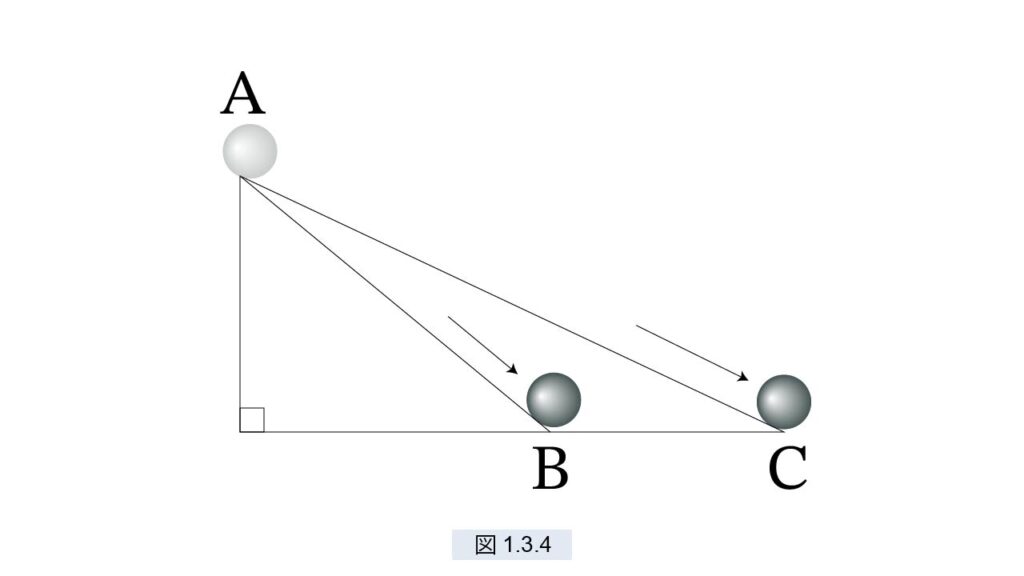
図1.3.4の直角三角形で、A から 球を転がしたときの B での速度と、C での速度は等しいということです。ガリレオの公準については次節で詳しく議論します。現在の私たちにとっては見過ごしやすいのですが、物理学が何もなかった時代これはすばらしい発見と言えます。一見関係のなさそうな振り子の運動も、ガリレオの頭の中では落下と結びついていたのです。

決定打となる実験

高台と坂の実験

直角三角形ABFの頂点 A から球を転がします。坂はテーブルの上に置かれていて、球は B で水平に打ち出されます。B 衝突が起きないよう滑らかになっています。坂の高さを AF ＝ S、テーブルの高さを BE＝h とします。球の落下地点を C、CE ＝ D’ とします。

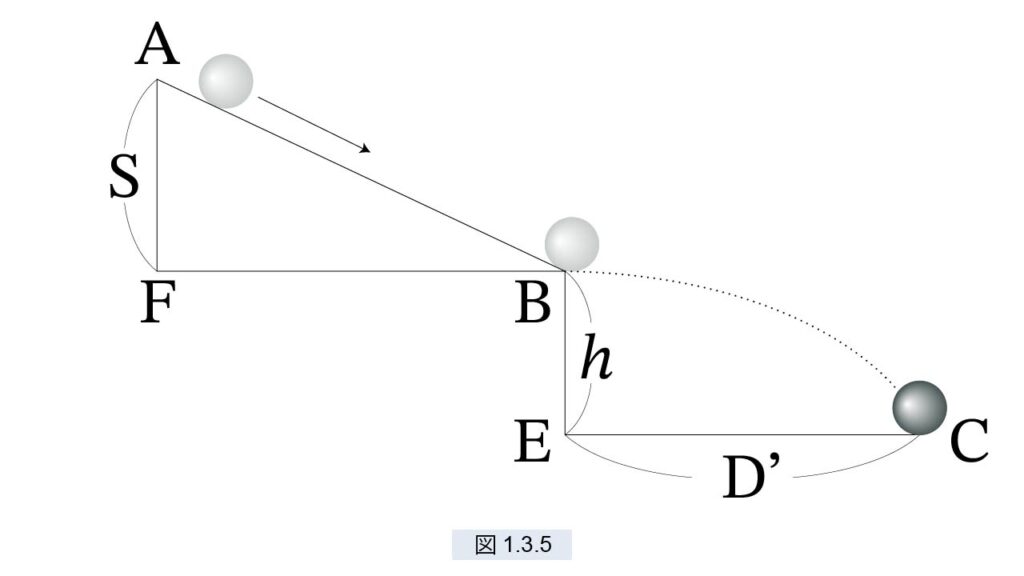
球の B での速度は坂の傾斜には関係なく、高さ S だけで決まります。また、大砲の水平発射 で明らかになったように、球の落下時間は、高さ h には関係なく常に一定です。 ガリレオは、h＝828, S＝ 300, 600, 800, 828, 1000 として実験をして次の結果を得ました。単位はプント（1プント ＝ 0.094 cm ≒ 1 mm ）です。( 表1.3.1 – 手稿 116v に記されたデータ群 )

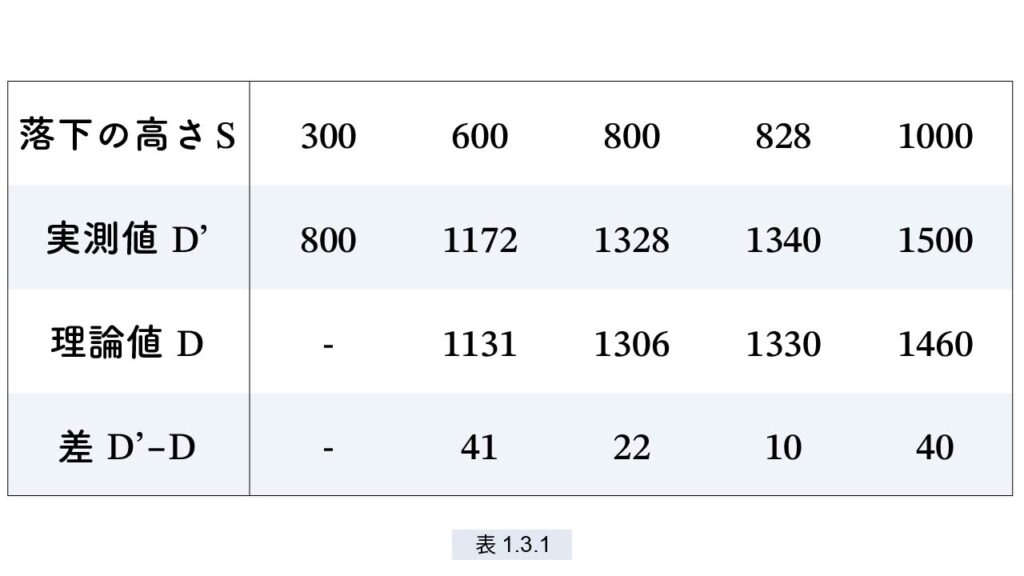
テーブルの高さを h＝828 と決めたのは、最初の S＝300 のときの飛距離を 800 ときりのよい数値にするためです。また、S＝828 を実験したのは、S＝h の場合どうなるかを調べたかったためだと思われます。 ガリレオは、「D は  √Sに比例する」という予測を立てたと思います。理論値 D を現在の我々の記号で書くと

\( d = 800 \times \sqrt{ \frac{s}{300} } \)

となりますが、ガリレオはまだ小数を知りませんから

\( D = \sqrt { (S \times 800 \div 300 ) \times 800 } \)

この D の値は、小数部を無視すれば現在の d と一致します。表1.3.1 では、差 D’ – D を計算していますが、誤差という点からすると

(D – D’)/D

を見たほうがよいでしょう。誤差は 3% ほどなので、予備的な実験としては良い結果だと思われます。

ガリレオは「長さ」や「平方根」をどのように扱っていたか

ここで注意しておきたいのは、ガリレオは長さを自然数で測っていることです。これは古代の幾何学にはなかったことです。現在の私たちは、長さとか面積というとすぐに数値を考えますが、ガリレオの時代の人々は小数も分数も知らなかったことに注意してください。ガリレオにとって、長さや面積は数値ではなく抽象的な“量”なのです。長さ a の平方とは、a×a ではなく、一辺が a の正方形の面積のことであり、面積 A の「平方根」とは、面積が A の正方形の長さのことなのです。日常が数で囲まれている私たちにとっては、このことはなかなか理解が難しいかもしれません。

ガリレオは自然数で表せない長さがあることを認識しており、一般には幾何学的な“長さ”で議論しなくてはならないと考えていました。上で扱った√Sの S は自然数に限ります。つまり一般の長さに関しては、“平方根”という考え方ではなく全く別の幾何学的な方法をとらざるを得なかったのです。