1-1.代数とアルゴリズムの語源

フワーリズミー：アルゴリズムと代数の起源

おそらく皆さんはアルゴリズムという語をご存知だと思います。このアルゴリズムという語と、代数の英語版のアルジェブラという語は、“フワーリズミー”という人物の名から来ています。フワーリズミーは9世紀のペルシアの数学者で、多くの著作がありますが、特に『インド数字による計算法』と『ジャブルとムカーバラによる計算法についての簡約な書』が有名で、これらの著作は数学の発展に大きな役割を果たしました。

『インド数字による計算法』は、現在私たちが使っている算用数字 0, 1, 2, …, 9 を使った10進数の掛け算や割り算などの四則演算や、開平などの計算方法の解説書です。現在の算用数字をフワーリズミーはインド数字と呼んでいますが、ヨーロッパではアラビア数字と呼ばれてきました（最近はインド・アラビア数字と呼ばれています）。ヨーロッパでは中世の終わりごろから、十字軍遠征をきっかけにして地中海交易が盛んとなり、アラビアの書物が多数ラテン語に訳されるようになります。その中で特に有名なのが上で挙げた『インド数字による計算補法』です。そのラテン語訳による解説書では、「アルゴリスミはこういった」という語句がよく使われるようになります。このアルゴリスミとはアル=フワーリズミーのラテン語訳で、“アル=”はアラビア語の定冠詞です。このインド式算術の書物があまりにも有名となり、とうとうフワーリズミーという人名がアルゴリスミという算術演算を表すようになり、やがてアルゴリズムという数学的手続きを表すように変わっていったのです。

代数の英語のアルジェブラは、もう一方の著作 『ジャブルとムカーバラによる計算法についての簡約な書』の題名から来ています。「ジャブルとムカーバラ」とは式の変形規則のことで、これも定冠詞“アル=”を付け「アルジャブル」、「アルムカーバラ」と呼ばれます。この理論はこれ以後フワーリズミーの後継者たちによって著しく発展させられますが、後継者たちはこの理論を「ジャブル学」と呼んでいました。やがてこの理論も西洋移入され、アルジャブル、アルジェブラと変化しました。アラビア数学を西洋に紹介したフィボナッチはアルゲブラと呼んでいます。フワーリズミーが「代数学の祖」と呼ばれるのは、このようなゆえんによります。

代数学の科学革命への貢献とその語源

フワーリズミーが始めた代数学は、近世ヨーロッパが科学を大発展させた科学革命にとって、なくてはならない理論的基礎を与えました。カッツは名著『数学の歴史』（共立出版 (2005)）の中で次のように述べています。

では“代数”とは何でしょうか。文字通りの解釈は「“数”に“代わるもの”」です。この“代数”という言葉は、とてもぴったりとした命名ですが、この語自体は英語の教科書“algebra” を中国語に訳す際、訳者のアレグザンダー•ワイリーと李善蘭が訳書のタイトルとして『代数学』(1859) としたことからきています。

ではジャブルとムカーバラがどのような操作かを見てみましょう。

ジャブル

フワーリズミーが扱うのは方程式、つまり2つの式を等号で結んだ等式です。左側の式を左辺、右側の式を右辺といいます。
ジャブルのもともとの意味は「（折れた骨などを）もとに戻す」こと、つまり「復元する」ということです。方程式では、マイナスのついた項があるとき、その項を両辺に加えると、その項が消えて反対側の辺にプラスとして復元できます。たとえば、

              5x² ＋ 8 – 10x ＝ 3

は、両辺に 10x を加えると

              5x² ＋ 8 ＝ 3 ＋ 10x

となります。ただし、フワーリズミーは、まだ“負の数”という概念は持っていません。上で「マイナスの付いた項」と述べたのは「引き算の項」のことです。つまりジャブルとは、引き算の項を移項して足し算にすることなのです。

ムカーバラ

ムカーバラは、「向かい合わせる」という意味で、式の両辺から等しい量を取り去って、式を簡約することです。たとえば、

              5x² ＋ 8 ＝ 3 ＋ 10x

の両辺から 3 を引くと

              5x² ＋ 5 ＝ 10x

となります。また両辺に共通の因数があるときに、それで割って簡約したり、分数を消去するために等式の両辺に同じ数を掛けたりすることもあります。たとえば、

5x² ＋ 5 ＝ 10x  ⇒  x² ＋ 1 ＝ 2x

なども簡約です。以降では、ジャブルを移項と、ムカーバラを簡約と訳し、アル=ジャブル学を代数と訳すことにします。

数の概念の変遷と同次元の制約

このシリーズでこれまでも見てきたように、“数”の概念は時代とともに変わってきます。『原論』の幾何学では数値計算は扱いません。“数”とは自然数を意味し、長さや面積は“量”として、数とは別ものとして扱っています。また、平方（square）とは正方形（の面積）のことで、正方形と線分（の長さ）は足すことはできません。点は0次元、線分は1次元、面積は2次元、体積は3次元と見なされるようになってきます。

「次元の異なるものは演算ができない」という規則を「同次元の制約」といいます。16世紀になってヨーロッパで方程式が議論されるようになっても、ヨーロッパではこの制約が守られていました。しかしフワーリズミーは、この時代にすでに完全にこの制約を無視しています。次にこれを見てみましょう。

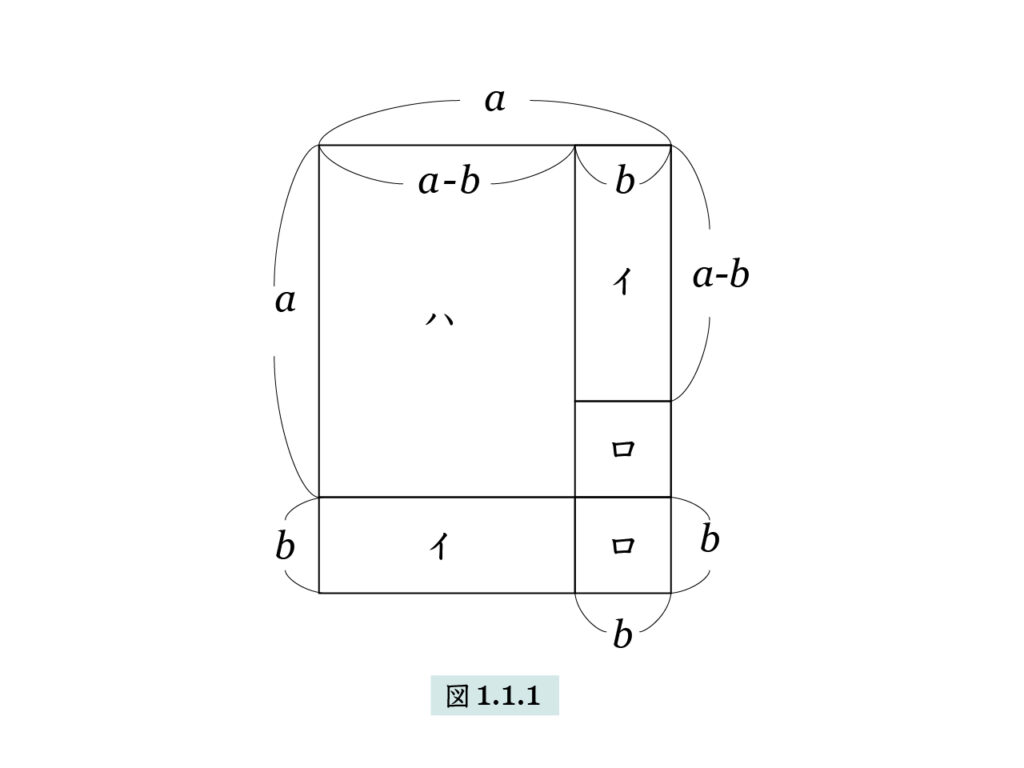
次章で詳しく述べますが、フワーリズミーは2次方程式の解法を、図を使って示しています。たとえば私たちがよく知っている公式

      (a+b) ×（a-b） = a² – b² (1)

を、図1.1.1のようにして説明しています。(1) をギリシアの幾何学では

      □(a＋b, a – b) ＝ □²(a) – □²(b) (2)

と表します。式 (1) で a と b は数であり、したがって (1) は代数の公式となります。一方 (2) は、左辺が表す面積が右辺の著わす面性と等しいことを述べてはいますが、代数の公式ではありません。(2) に現れる a と b は一般の数ではなく辺に限り、左辺の“ー” は辺の差で、右辺の“ー”は面積の差です。

フワーリズミーは、“式”を“数”と同等のものとして扱っています。じっさい、式 100＋x² – 20x と 50＋10x – 2x² を足して、次のように言っています。

同次元の制約を完全に破っています。

フワーリズミーは方程式を考えることによって、数の概念を拡張していきます。割り算の問題として次の3つの問題を取り上げています。

 ・面積が 30 の畑がある。幅が 5 なら長さは？
 ・30歳の男は、息子の5倍の年齢である。息子の年齢は？
 ・重さ 30の布地を同じ重さの5本の布巻に裁断した。それぞれの布巻の重さは？

現代の私たちにとっては、この問題のどこが難しいのか理解できないかもしれません。しかし、面積、年齢、重さといった異なる量の意味、その割り算の意味を考えると、途端に難しい問題となるように思います。フワーリズミーは、「量は数である」とし、上の問題はすべて方程式

            5x ＝ 30

を解く問題である、としました。この方程式の解法はもちろん割り算

              30 ÷ 5

です。方程式は、問題の意味や数値の違いを超えて、常に正しい解法を導いてくれる、とフワーリズミーは解説しています。

代数の概念と歴史的発展

では、“代数とは何か”をまとめておきましょう。フワーリズミーの後継者のサマウアルは次のように述べています。「算術家が既知量に対して算術的道具を使うように、未知の量に対して同じように算術的道具を使うこと」

現代数学の創始者の一人とみなされているオイラーは、1770年の著書『代数学入門』で代数学というものを次のように述べています。

オイラーは、フワーリズミーからほぼ千年も後の人ですが、フワーリズミーはすでにオイラーと同じ考えにたどり着いていました。