How the Ancient Egyptians Calculated Area: Precision and Ingenuity in Early Mathematics
Egyptian circle math provides insight into how ancient civilizations approached geometry.
The “Father of History,” Herodotus,* once famously stated:

The Greeks learned mathematics from the Egyptians.
However, for a long time, European scholars largely dismissed this claim. Many asserted that only the most basic forms of mathematics were used in pyramid construction, or belittled the Egyptian fraction system as strange and primitive.
It’s only in recent years that we’ve come to appreciate the sophistication of ancient Egyptian mathematics. In the previous section, we saw how the Egyptians were able to solve quite complex problems involving ratios. This time, let’s explore how they calculated area.
Practical Mathematics and Land Surveying in Ancient Egypt
Egyptian geometry emerged from the need to measure land after the annual flooding of the Nile and to redistribute farmland among peasants. More broadly, mathematics is believed to have developed as a practical tool—for managing agricultural yields, overseeing redistribution, and calculating the amount of stone needed for pyramid construction.
As in the previous section, this chapter examines problems found in ancient papyri. When converted into modern metric units, these problems may seem elementary and simple to us. However, here we will explore them using the original Egyptian units. This approach helps us understand how ancient people conceived numbers, and how they gradually developed the concepts of number and area.
Surveying Units and Farmland Area Measurement in Ancient Egypt
As described in 3-1. How Numbers and Units Were Handled in Ancient Egypt, units of length included the cubit (arm’s length), palm (hand’s breadth), and digit (finger’s width). In this section, we add another unit called the rod ket.
1 rod ket = 100 cubits = approximately 50 meters
(1 cubit = approximately 0.5 meters)
In ancient Japan as well, long bamboo poles were used for land surveys during cadastral registration. Ropes were likely avoided because they could bend or sag. Since 1 rod ket equals about 50 meters, it was probably measured over multiple segments.
The units of area were defined as follows:
1 field (setat) = 100 strips = 10,000 square cubits = 1 square rod
1 strip (peikes) = 1 cubit × 1 rod ket = 100 square cubits
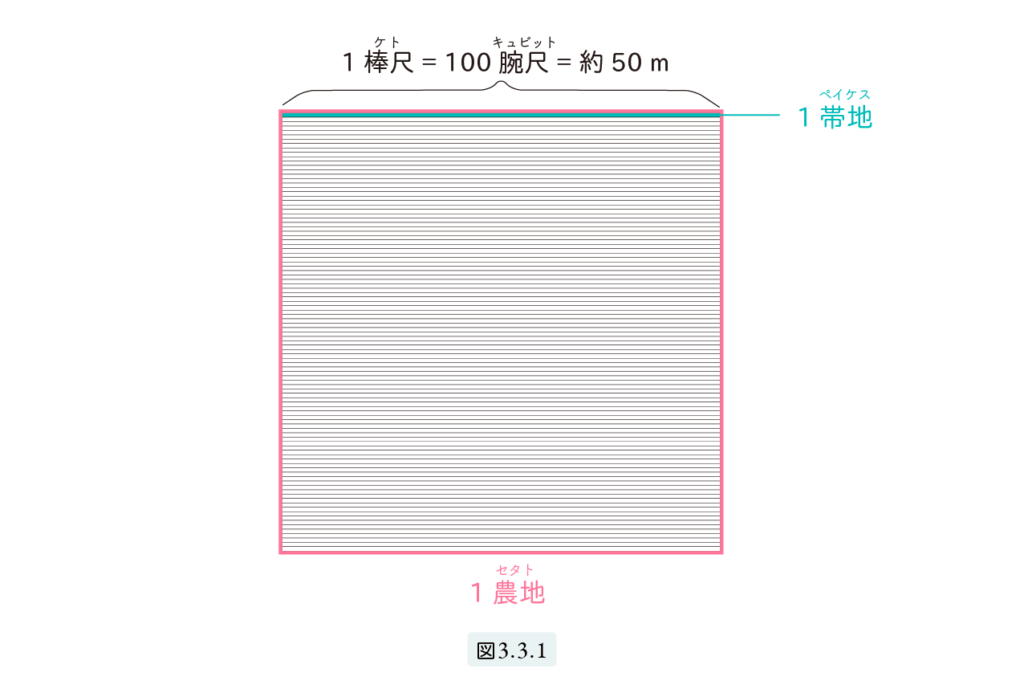
In ancient Egypt, area was measured using a long, narrow strip of land measuring 1 cubit in width and 100 cubits in length.
This unit was called 1 strip (peikes). Fields were divided into rectangular plots by surveyors, with a fixed width of 100 cubits, or 1 rod (ket). Therefore, only the length of the field needed to be measured to calculate its area. (See Figure 3.3.1.)
If the length was n cubits, then the field contained n strips, or n peikes. Since 100 peikes made 1 field (setat), area was effectively treated as a count of strips. This system was intuitive and highly practical for measuring and distributing farmland.
However, it must have taken a long journey of thought to arrive at the now-familiar formula:
Especially when using mixed units like rods (ket), cubits, palms, and digits, performing multiplication alone would have been quite a challenge.
Most of you today accept formula (1) without question. That is perfectly fine—but let’s take a moment to reflect on how multiplication itself came to be understood.
Using Small Rectangles as the Foundation of Area Calculation
Multiplication likely originated as an extension of addition. The n-fold of a number a, that is, n × a, was understood as “a added n times.”
As noted above, the area of farmland was measured by how many strips (peikes) it contained.
The Egyptians extended the concept of number from natural numbers to fractions. So when a length was expressed as a fraction, how would they have interpreted formula (1)?
Since the Egyptian unit system is complex, let us consider this in modern meters.
Suppose we have a piece of land that measures:
What is the area of this land?
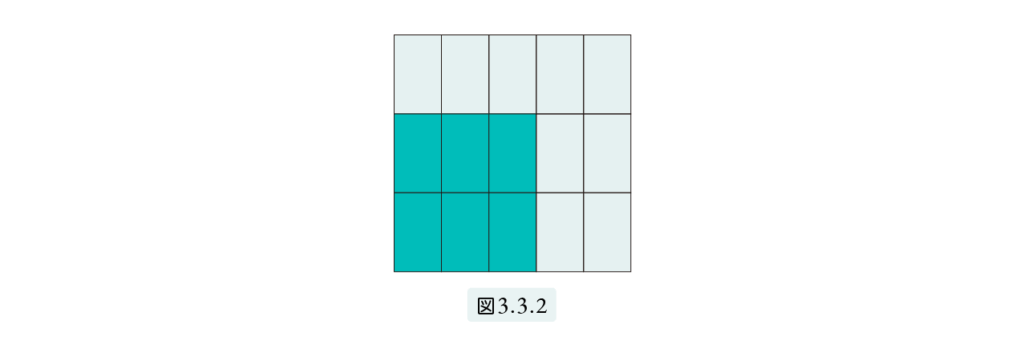
When a 1-meter square piece of land is divided as shown in Figure 3.3.2—into thirds vertically and fifths horizontally—it creates small rectangles measuring
$$\frac{1}{3} \text{ m} \times \frac{1}{5} \text{ m}.$$
There are
$$3 \times 5 = 15$$
of these small rectangles in total.
Each one represents
$$\frac{1}{15}$$
of the full square meter.
Now consider a rectangle with dimensions
$$\frac{2}{3} \text{ m} \times \frac{3}{5} \text{ m}.$$
This rectangle contains
$$2 \times 3 = 6$$
of those small rectangles.
So the shaded area is:
$$\frac{6}{15} = \frac{2 \times 3}{3 \times 5} = \frac{2}{5} \text{ m}^2.$$
Even when the lengths are arbitrary fractions, this method can be generalized. It is likely that the Egyptians, by solving various problems with concrete values, came to recognize that the formula
was valid.
From here on, we will assume the unit of length is the rod (khet) and the unit of area is the field (setat).
Note that:
This modern notation “khet²” is a shorthand for “square rod.” Now, let us look at problems that appear in the papyri.
Even when the lengths are arbitrary fractions, this method can be generalized. It is likely that the Egyptians, by solving various problems with concrete values, came to recognize that the formula
was valid.
From here on, we will assume the unit of length is the rod (khet) and the unit of area is the field (setat).
Note that:
This modern notation “khet²” is a shorthand for “square rod.” Now, let us look at problems that appear in the papyri.
Let’s Solve Ancient Egyptian Area Problems
A rectangular plot of land has an area of 12 setat (Egyptian units of area), and its length is \( \frac{1}{2} ; \frac{1}{4} \) of its width.
Find the length and width of the rectangle.
Note: 1 setat = \( (\text{1 rod-length})^2 \)
Let’s first solve this using a modern-style equation. Consider a square plot of land with side length \( x \) rods (ket). The Egyptian fraction \( \frac{1}{2} ; \frac{1}{4} \) can be converted to the regular fraction \( \frac{3}{4} \).
For a rectangle with width \( x \) rods and height \( \frac{3}{4}x \) rods, the area is 12 square rods (ket2). This gives us the equation:
\[ \frac{3}{4} x^2 = 12 \tag{2} \]
This is a quadratic equation in terms of \( x \). You can solve it by multiplying both sides of equation (2) by the reciprocal of \( \frac{3}{4} \), which is \( \frac{4}{3} \), to obtain:
\[ x^2 = 12 \times \frac{4}{3} = 4 \times 4 \]
Since the ancient Egyptians did not use equations, they likely solved this in a different way. Given that the vertical side is \( \frac{1}{2} ; \frac{1}{4} \), they probably divided the square in half, then halved it again as shown in Figure 3.3.3. The shaded rectangle would then represent \( \frac{3}{4} \) of the square.
The square is \( \frac{3}{4} \) the size of the rectangle: \[ \text{Square} = \frac{3}{4} \times \text{Rectangle} \tag{3} \]
Also, as clearly shown in the figure, the square is 4 times the \( \frac{1}{3} \) of the rectangle: \[ \text{Rectangle} = \frac{4}{3} \times \text{Square} \tag{4} \]
Comparing equations (3) and (4), we can see that the reciprocal of \( \frac{3}{4} \) is indeed \( \frac{4}{3} \). In fact, the Egyptians calculated the area of the square as:
\[ 12 \times \frac{4}{3} = 16 \]
Therefore, the side length \( x \) of the square is:
\[ x = 4 \]
Today, we calculate the reciprocal of a fraction simply by flipping the numerator and denominator. However, in the case of Egyptian fractions, this process is a bit more complicated. Through solving practical problems over and over, the ancient Egyptians gradually developed the concept of a “reciprocal” and learned how to apply it in their calculations. This approach—deriving general rules from specific examples—is known as the inductive method. In Figure 3.3.4, let us assume that c = 1 rod-khet.
a strip-pēkes + b strip-pēkes = (a + b) strip-pēkes
The Egyptians likely realized that there was no need to restrict c to exactly 1 rod-khet.
They also recognized that, regardless of units like rod-khet or strip-pēkes, the following holds true for any numbers a, b, and c:
(a + b) × c = a × c + b × c (5)
This rule could then be generalized into the following insight:
“The area of two rectangles with the same width is proportional to their heights.”
How the Ancient Egyptians Approached the Area of a Circle
Since the mystery of the pyramids is said to involve the concept of π (pi), let us now look at how the Egyptians dealt with the area of a circle. In excavated papyri, there is a diagram (as shown in Figure 3.3.5) depicting a circle alongside an octagon formed by cutting the corners off a square with a side length of 3.
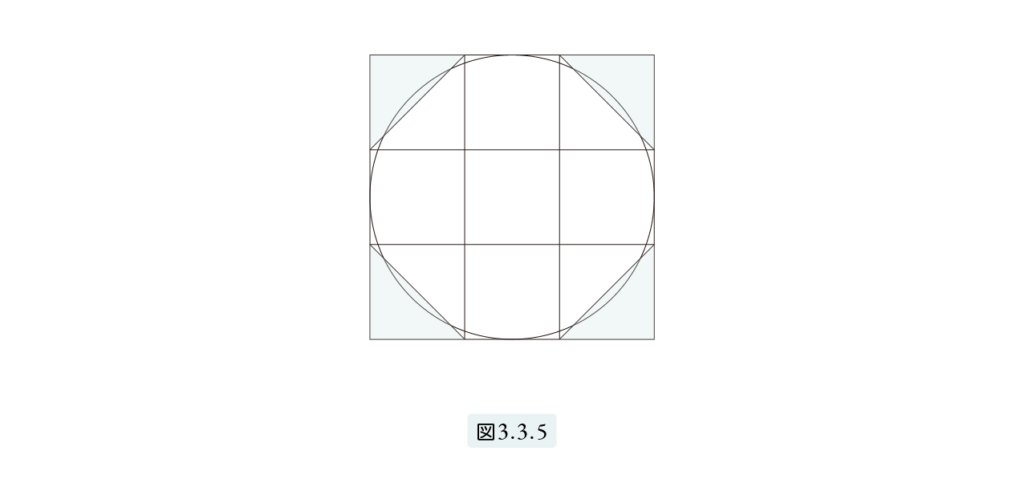
Because the area of the octagon closely matches the area of the circle, scholars believe that this diagram was used to represent the area of a circle. For easier calculation, let’s assume the square has a side length of 9 instead of 3. Then, the area of the square is 81, and the shaded corner areas total 18. Subtracting those, we get the area of the octagon as 63.
The Egyptians approximated this as 64, which is 82, making the math easier. In other words:
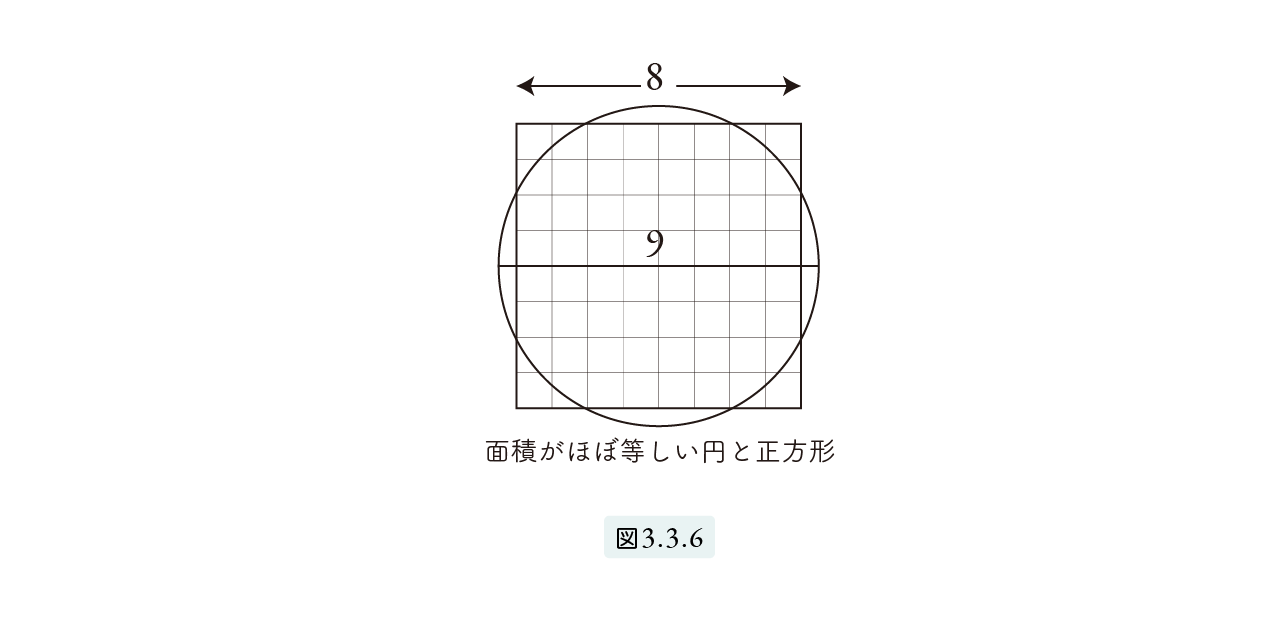
The area of a circle with diameter 9 = the area of a square with side 8.
Take a look at Figure 3.3.6 to compare a circle with diameter 9 and a square with sides of 8.
How Much Did the Ancient Egyptians Know About the Properties of a Circle?
The ancient Egyptians understood that the area of a circle is approximately 64/81 of the area of its circumscribed square. In other words, they recognized that the area of a circle is proportional to the area of the square that encloses it. This implies that they had a practical grasp of the concept of ratio. Note that this formula applies to area, not to circumference.
The mathematical proof that “a circle’s circumference is proportional to its diameter” and that “a circle’s area is proportional to the area of its circumscribed square”—and, more importantly, that these two ratios are equal—was first provided by the Greeks. It was Archimedes who proved that both values are, in fact, the same. We will discuss this further in Chapter 4.

