The Concept of Ratios and Ancient Mathematics
In this section, we will take a closer look at how ratios and slopes (the seked) were handled in ancient Egypt.
Ratios are all around us in daily life—such as a 10% consumption tax, a 50% discount at a sale, or a 30% chance of rain tomorrow. The concepts of ratios, proportions, and proportionality are among the most fundamental ideas in mathematics. Constants like pi (π) and the golden ratio (φ) are also types of ratios. But to what extent did the ancient Egyptians understand these concepts?
In the Greek mathematical work Elements, there is a clear definition of ratios, and a sophisticated “theory of ratios” is developed—one that stands up even by modern mathematical standards. Elements was a remarkable work compiled by Euclid and can be considered the first mathematical text written to be read and studied by others.
On the other hand, the surviving Egyptian mathematical documents that have been unearthed seem to have been textbooks for scribes—similar to modern-day exam preparation workbooks—consisting mostly of problem sets without formal exposition. Therefore, it is not appropriate to directly compare Egyptian and Greek mathematics based solely on these records.
Ratio Problems Solved by the Ancient Egyptians
Judging from the papyri unearthed in Egypt, ratio-related problems like the following seemed to be very simple, everyday exercises for the ancient Egyptians:
- If 3 loaves of bread are distributed among 4 people, how many loaves are needed for 10 people?
- If 4 kilograms of wheat can produce 3 liters of beer, how many liters of beer can be made with 10 kilograms of wheat?
- If a slope rises 3 meters for every 4 meters traveled horizontally, how many meters will it rise after traveling 10 meters horizontally?
All of these problems share the same logical structure.
When learning new concepts, we often struggle, but grouping similar ideas together can make them easier to remember.
These problems can all be organized under the concept of ratios.
Today, we can use algebraic equations to solve such problems.
Using an unknown variable x, the above three problems can be expressed as follows:
- The ratio of 3 loaves to 4 people is equal to the ratio of x loaves to 10 people.
- The concentration of beer made from 4 kilograms of wheat yielding 3 liters is equal to the concentration of beer made from 10 kilograms yielding x liters.
- The slope rising 3 meters for every 4 meters traveled is equal to the slope rising x meters after traveling 10 meters.
All three problems can be illustrated using graphs like the one shown in Figure 3.2.1.
In Problem 3, the graph represents an actual slope.
In this graph, for every unit traveled horizontally to the right, the elevation increases by \frac{3}{4}.
This \frac{3}{4} is called the slope of the graph.
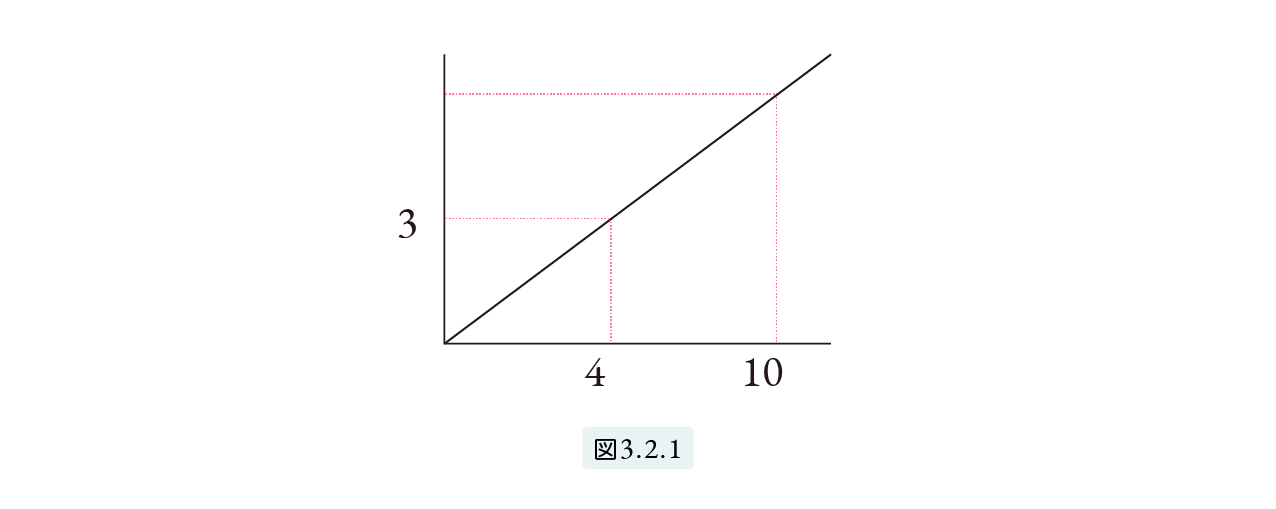
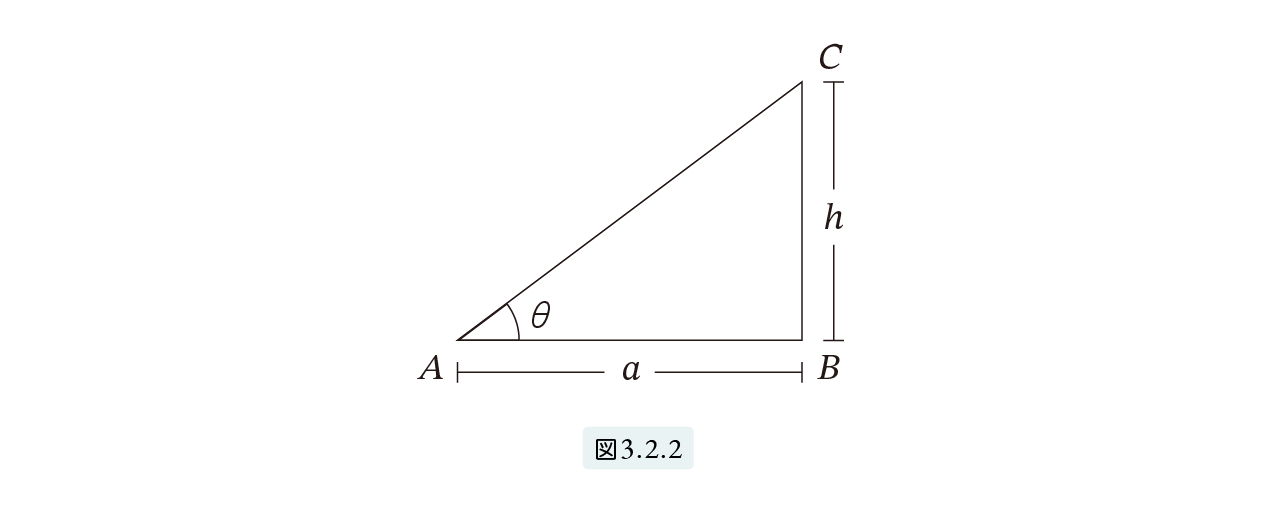
Consider the right triangle \( ABC \) as a slope. We measure the steepness of this slope — in other words, the degree of inclination — using the fraction \( \frac{h}{a} \). This expresses that for every horizontal distance of \( a \), the vertical rise is \( h \).
In other words,
\[ \text{Slope} = \text{Length risen per 1 unit traveled horizontally} \]
When a road sign indicates a slope of 5%, it means that for every 100 meters traveled horizontally, the elevation increases by 5% of 100 meters — that is, by 5 meters.
Relationship Between Seked (Slope) and Modern Slope
Take another look at Figure 3.2.2. In the right triangle \( ABC \), if the angle \( \theta \) is known, then the slope \( \frac{h}{a} \) can also be determined.
This can be easily found by using a table of trigonometric functions (tangent table) or a scientific calculator. The function \( \tan \) is read as “tangent.” For example, if \( \theta = 45^\circ \), pressing the calculator key for \( \tan(45) \) gives the result 1.
Conversely, to find the angle from the slope, you use the function \( \tan^{-1} \), which is called the “arctangent.” You don’t need to understand exactly what the \( \tan \) function is. It’s enough to know that “given an angle \( \theta \), the slope can be obtained.” Of course, the ancient Egyptians did not know about \( \tan \); this is simply for your modern calculations.
The Egyptians measured the steepness of a slope by using the reciprocal of the slope, namely \( \frac{a}{h} \).
What may be confusing for us is that the Egyptians used different units for the base and height. The base was measured in palms (palm-lengths), while the height was measured in cubits.
More precisely, the gentle incline of a slope was expressed as:
\[ \text{Seked} \times \text{palm} = \text{“Move horizontally by } x \text{ palms to rise } 1 \text{ cubit vertically”} \]
Since it’s confusing when the units differ, for simplicity, we will measure both the base and height in cubits from now on.
In Figure 3.2.2, if both \( a \) and \( h \) are measured in cubits, then \( a \) cubits is equivalent to \( 7a \) palms. Thus, the Seked of this slope is:
\[ \text{Seked} = \frac{7a}{h} = 7 \times \frac{\text{base}}{\text{height}} \tag{1} \]
We will regard equation (1) as the definition of “Seked ~ palms.”
From now on, we will omit “palms” and simply write “Seked ~.”
For you, it is easiest to remember the following simple formulas: Slope and Seked are reciprocals of each other, but when converting, don’t forget to multiply by 7.
\[ \text{Slope} = \frac{7}{\text{Seked}}, \quad \text{Seked} = \frac{7}{\text{Slope}} \tag{2} \]
Problems on the Seked Found in Papyri
The following problems were actually found in excavated ancient papyri.
Let’s use them as practice problems and see how much calculation ability the ancient Egyptians had.
Problem 3.2.1
A pyramid has a height of 250 cubits and a base side length of 360 cubits.
What is the seked of this pyramid?
When we redraw the structure as a right triangle, the base is 180 cubits and the height is 250 cubits.
Therefore, the seked (calculated by multiplying the reciprocal of the slope by 7) is:
\[ 7 \times \frac{180}{250} = \frac{126}{25} = 5 + \frac{1}{25} = 5;\frac{1}{25} \]
Thus, the seked of this pyramid is 5;1/25 palms.
Additionally, let’s calculate the slope and the angle:
- Slope = \( 7 \times \frac{25}{126} = \frac{175}{126} = 1.3888888889 \)
- Angle = \( \tan^{-1}(1.3888888889) = 54.24611275 \) degrees = 54 degrees 14 minutes 46 seconds
Problem 3.2.2
There is a pyramid with a base length of 140 cubits and a seked of 5 palms 1 digit. What is its height?
First,
\[ 5\ \text{palms}\ 1\ \text{digit} = 5\ \text{palms} + \frac{1}{4}\ \text{palm} = 5;\frac{1}{4}\ \text{palms} \]
Since 1 digit equals \( \frac{1}{4} \) palm, the seked is \( 5;\frac{1}{4} \) palms.
Applying formula (1) again:
\[ 7 \times \frac{\text{base}}{\text{height}} = 5;\frac{1}{4} = \frac{21}{4} \]
Thus,
\[ \text{height} = 7 \times \text{base} \div \frac{21}{4} = 7 \times 70 \times \frac{4}{21} = 70 \times \frac{4}{3} = 93;\frac{1}{3} \]
Therefore, the height is \( 93;\frac{1}{3} \) cubits.
Problem 3.2.3
There is a pyramid with a base length of 140 cubits and a height of 93;1/3 cubits. What is the seked?
This problem deals with the same pyramid as in Problem 3.2.2. Therefore, the answer is a seked of 5 palms 1 digit.
In the excavated papyri, it is common to find problems like these two that share the same answer. This likely served as an educational measure to help students learn the method of solving them.
Originally, the purpose of the seked was to find the base when the height is given.
In other words, multiplying the height by the seked yields the base.
However, in Problem 3.2.2, we are instead asked to find the height from the base.
To solve this, “division of fractions” is necessary.
Even today, division with fractions can be difficult to grasp, yet the ancient Egyptians were able to carry out division using Egyptian fractions.
This demonstrates that they had a thorough understanding of the concept of fractions.
Problem 3.2.3
There is a pyramid with a base length of 140 cubits and a height of \( 93;\frac{1}{3} \) cubits. What is its seked?
This problem deals with the same pyramid as in Problem 3.2.2. Therefore, the answer is the same: the seked is 5 palms 1 digit.
In excavated papyri, it is common to find problems like these two where the answers are shared. It is thought that this was a deliberate educational strategy to help learners memorize solution methods.
Originally, the seked was intended to find the base length given the height.
In other words, by multiplying the seked by the height, one obtains the base length.
However, in Problem 3.2.2, the reverse calculation is performed: finding the height from the base.
To solve such a problem, it is necessary to use “division of fractions.”
Even today, division involving fractions can be challenging to understand, but the ancient Egyptians were capable of performing division using Egyptian fractions.
This means they had a sufficiently deep understanding of the concept of fractions.
Problems 3.2.1 to 3.2.3 are actual problems found in the Rhind Papyrus, an ancient mathematical document.
From this, we can understand that the Egyptians used the concept of seked to design the construction of pyramids.
For the Egyptians, calculating the height of a pyramid from its base length and seked was a simple exercise.
The Seked of the Great Pyramid of King Khufu
Let’s calculate the seked of the Great Pyramid of King Khufu, as mentioned in “1-1. The Mystery of the Pyramids.”
Although the seked is originally defined using the ancient Egyptian units of cubits and palms, it represents a ratio, so we can calculate it today using meters or by applying the concept of slope.
Although the stones on the surface and the apex of the Great Pyramid are missing, the slope can be estimated from the remaining stones.
Most sources state the angle as 51 degrees 50 minutes, though some specify it more precisely as 51 degrees 50 minutes 40 seconds.
First, let’s convert these degree-minute-second measurements into decimal degrees:
51 degrees 50 minutes = 51 + 50/60 degrees = 51.833333 degrees
51 degrees 50 minutes 40 seconds = 51 + 50/60 + 40/3600 degrees = 51.844444 degrees
The slope for an angle θ can be calculated using tan(θ).
The seked can then be calculated using the formula from earlier (2):
Seked = 7 ÷ slope
Calculating:
tan(51.833333) = 1.272295703 → seked = 5.50186 palms
tan(51.844444) = 1.272803663 → seked = 5.49967 palms
Whichever value you use, the seked of King Khufu’s Great Pyramid can be considered approximately 5;1/2 palms (5 and one-half palms).
Although modern tools like tan and angle measurements are used here, it shows that the seked can be determined without needing the ancient length units.
It has been confirmed that the Egyptians used the concept of seked in the design and construction of the pyramids, and that the seked of the Great Pyramid is expressed by the simple Egyptian fraction 5;1/2.
What Are “Pes” Problems?
We have learned that the ancient Egyptians expressed the slope of an incline using a ratio called the “seked.” However, from the seked alone, we cannot conclude that they had fully mastered the concept of “ratio.” Next, let’s consider problems known as “Pes problems.”
At the beginning of this article, we looked at problems involving the ratio between the amount of wheat and the amount of beer produced from it. In modern times, we usually think about how many kilograms of wheat are needed to produce one liter of beer. (It’s the same concept as population density or specific gravity.) However, in Egypt, they thought in the opposite way: “How many liters of beer can be made from one kilogram of wheat?” In other words, instead of focusing on concentration (strength), they thought in terms of dilution (weakness) from the product side. Also, the units used were not liters but Egyptian units.
Modern mathematics emphasizes understanding through form rather than meaning. Thus, whether it’s “height divided by base” or “base divided by height” is essentially the same. Similarly, the difficulty of a problem should not change whether the units are cubits or meters. However, when the units change or when the notion of concentration switches to dilution, many people suddenly feel the problem becomes harder.
In school, you may have been taught to “understand the meaning” when solving problems. While it is important to fully grasp one specific case, after that, it’s often easier to solve problems mechanically by applying formulas. In other words, while “understanding the meaning” is crucial, memorizing the “form” (that is, “formulas”) is also extremely effective for quickly handling many types of problems. Let’s test this idea with the following problems.
The term “Pes” comes from the word “pesi,” meaning “to cook,” and because the word “Pes” appears in the papyri, such problems came to be called “Pes problems.” “Pes” expresses the dilution of the wheat content in products like bread or beer, so we will call this the “dilution rate, or Pes.” It represents how diluted the wheat content is, not how concentrated.
The formula is as follows:
\[ \text{Pes} = \frac{\text{Number of products}}{\text{Amount of wheat used}} \]
For example, if 5 loaves of bread are made from 1 hekat of wheat, we say: “This bread has a dilution rate of Pes = 5.”
If the Pes is known, it is easy to determine how many loaves of bread can be made from a given amount of wheat. Today, we express rates with unit names like m/sec (meters per second). If we were to modernize the unit for Pes, it would be “pieces per hekat” for bread and “cups per hekat” for beer. However, in the following explanations, we will omit the “per hekat” part to match the ancient Egyptian notation.
Thus, the general formulas can be summarized as:
\[ \text{Pes} = \frac{\text{Pieces}}{\text{Hekat}} \quad \text{or} \quad \text{Pes} = \frac{\text{Cups}}{\text{Hekat}} \tag{3} \]
Problem 3.2.4
Problem 3.2.4: Using 3;1/2 hekat of wheat, 80 loaves of bread were made. Find the dilution rate, or Pes.
First, convert the Egyptian fraction 3;1/2 into a modern fraction:
\[ 3; \frac{1}{2} = \frac{7}{2} \]
Since “Pes = (Number of pieces) ÷ (Hekat),” the Pes is calculated by:
\[ 80 \div 3; \frac{1}{2} = 80 \div \frac{7}{2} = 80 \times \frac{2}{7} \]
Performing the calculation:
\[ 80 \times \frac{2}{7} = 22 + \frac{6}{7} = 22 + \frac{1}{2} + \frac{1}{3} + \frac{1}{42} \]
Thus, the final answer is:
\[ 22; \frac{1}{2}; \frac{1}{3}; \frac{1}{42} \]
Note that in this calculation, \( 80 \times \frac{2}{7} \) is converted into an Egyptian fraction. We omit the detailed explanation of how to perform this conversion here. However, please keep in mind that the Egyptians were capable of performing calculations involving the division of fractions.
—Omitted for brevity.—
Summary
Through the above discussion, it becomes clear that the ancient Egyptians had mastered not only the concept of slope, expressed through the seked measured in digits for pyramid inclines, but also the broader concept of ratios, such as the thinness of bread and beer represented by the pes. Furthermore, they accurately solved complex calculation problems using these concepts and expressed them with Egyptian fractions.
This is a characteristic not found in later Greek mathematics.

