Understanding Numbers Through Numeral Systems
When reading historical texts, we modern readers often interpret past events through the lens of contemporary thinking and moral values. However, people in ancient times frequently had completely different ways of perceiving the world. This is something we sometimes sense when reading myths or folktales. It’s important to note, though, that such traditional narratives have often been adapted and rewritten over time to match the sensibilities of each era. Likewise, historical events are interpreted differently depending on the period in which they are studied. A prominent historian once remarked, “History is the creation of historians.”
But what about numbers? How have they been understood and treated throughout human history?
Let’s briefly review the different types of numbers. Natural numbers—1, 2, 3, and so on—are used for counting quantities. When zero and negative numbers are added, we have the set of integers. Fractions composed of integers in both the numerator and the denominator are called rational numbers. Real numbers that are not rational are known as irrational numbers. These are not strict definitions, of course. In ancient times, people often believed numbers existed inherently in the natural world and did not attempt to define them formally.
One well-known philosophical question, frequently quoted in literature, asks:
Were numbers invented by humans, or do they exist independently of us?
In the late 19th century, the mathematician Leopold Kronecker once stated:
“God made the natural numbers; all else is the work of man.”
However, shortly after, another mathematician, Giuseppe Peano, went on to define even the natural numbers in formal terms.
It is said that animals such as monkeys, dolphins, crows, and parrots can recognize small numbers. However, this recognition tends to be limited to small quantities. What about much larger numbers—such as millions or billions, or even huge numbers like 10⁵⁰ or 10¹⁰⁰? Understanding such large numbers requires the use of language and symbols. We use language to think. Without language, our capacity for abstract thought would be significantly restricted. And language, in turn, is recorded using written characters. The invention of writing didn’t just allow us to record speech—it accelerated the development of language itself. This is evident even in the way we represent numbers using symbols, known as numeral systems. To understand how people in ancient times thought, we need to understand the language and script systems they used.
In Europe, Roman numerals were commonly used until the early modern period. These numerals, which you can still see on old clocks, represent numbers like this:
I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII
This system was accessible to the general public of the time, especially those less accustomed to memorizing large sets of symbols. However, Roman numerals were not suited to expressing or working with large numbers like millions or billions, and they only handled natural numbers. During the Renaissance, when figures like Leonardo da Vinci flourished, Arabic numerals—introduced from the Arab world—began to spread across Europe. These are the numerals we use today: 0, 1, 2, …, 9. With them came the decimal (base-10) system. Even then, however, calculations remained largely within the realm of natural numbers.
In fact, fractions and decimals did not become widely used in Europe until after the Renaissance. That means that neither the people of ancient times nor those of the Renaissance would have conceptualized values like pi (π ≈ 3.14…) or the golden ratio (φ ≈ 1.618…) in the way we do today.
Greek Mathematics and the Influence of the Ancient Orient
reek civilization has long held a central place in the European view of history. For centuries, it was considered the cradle of European culture, and mathematics was widely believed to have been born in Greece. However, with the progress in deciphering ancient scripts—such as Egyptian hieroglyphs on papyrus and Mesopotamian cuneiform—it has become increasingly clear that advanced forms of mathematics existed in earlier Oriental civilizations as well. This has led scholars to reconsider the narrative: Greek mathematics may have been significantly influenced by the mathematics of Egypt and Mesopotamia.
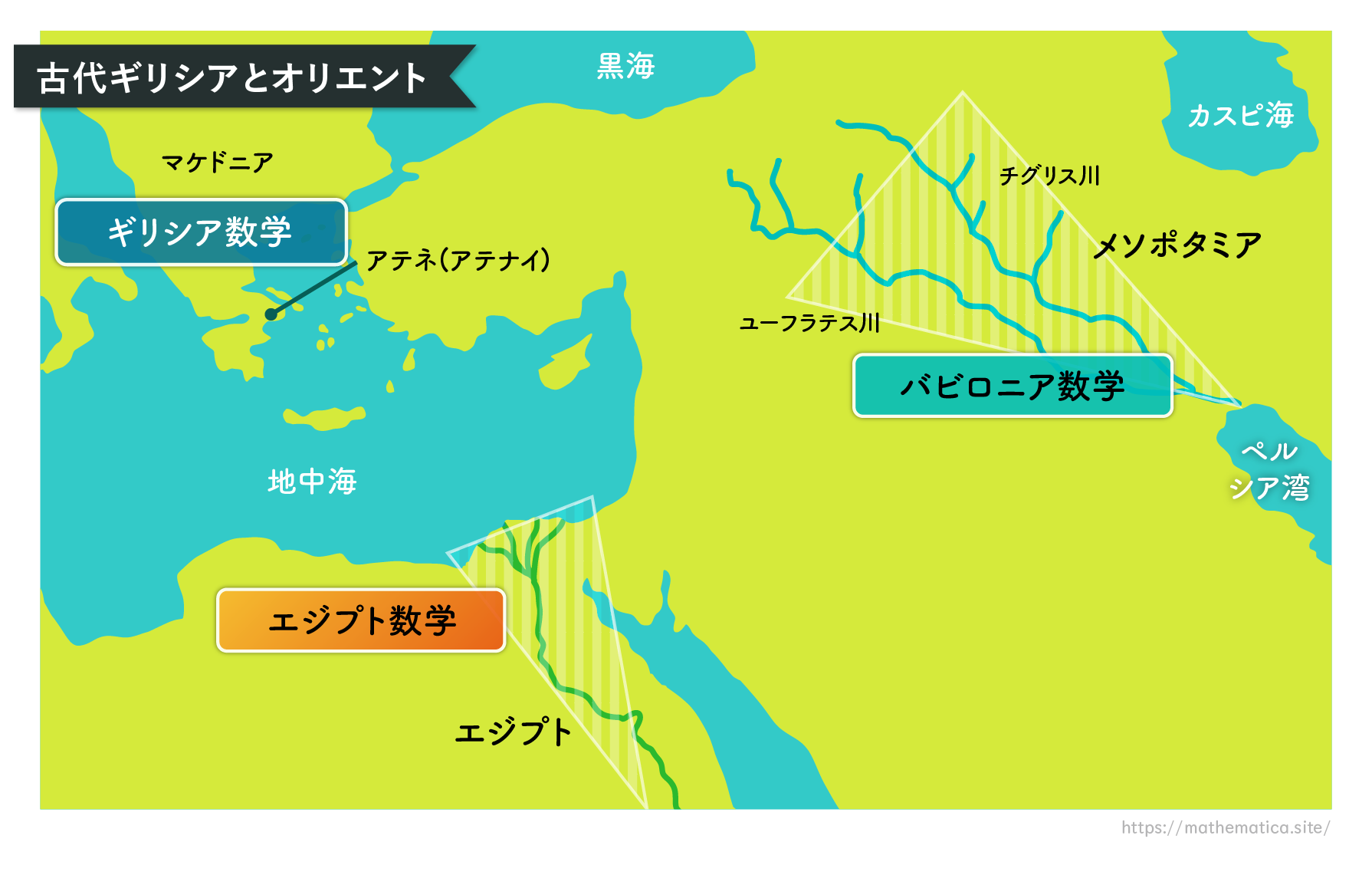
Today, Greek civilization is often seen not as a self-contained phenomenon, but as one part of a broader cultural network that extended across the eastern Mediterranean. In this broader context, the idea of Greek originality in mathematics is complemented by recognition of the intellectual richness of earlier Eastern traditions.
The mathematics developed in Mesopotamia is commonly referred to as Babylonian mathematics, a term we will adopt in this series as well. Below, we’ll briefly outline some features of Egyptian, Babylonian, and Greek mathematics.
The final dynasty of ancient Egypt was, in fact, ruled by a Greek-speaking monarch. As such, many of the terms used in this series are drawn from the Greek language. While modern academic works increasingly use reconstructed ancient Egyptian terminology, this series aims to offer a foundational introduction to the history of mathematics, so we will use terminology that is more widely familiar. For example, we refer to Egyptian rulers as “Pharaohs,” even though this term came into use after the Pyramid Age. For the sake of clarity and continuity, we use it throughout to refer to Egyptian kings.
Egyptian Civilization and the Rise of Greece
By the time Greek civilization began to emerge, Egyptian civilization was already entering a period of decline after thousands of years of cultural development. The Greek mainland, being mountainous and agriculturally limited, could not sustain its population through farming alone. As a result, the Greeks turned to maritime trade and colonization, establishing settlements across the Mediterranean. One key area of colonization was Anatolia (modern-day Turkey), where numerous Greek cities were founded.
Maritime trade during this period was not always peaceful—what began as commerce could sometimes turn into conflict. There are historical accounts of raids in which older individuals were killed and younger people were taken as captives or slaves. While such actions are clearly condemned by modern ethical standards, they were, unfortunately, commonplace in many parts of the ancient world and not typically viewed with the same moral framework as today.
The Greeks were renowned for their bravery and were often recruited as mercenaries. In one historical episode, a coastal Egyptian village was attacked by a group of Greek mercenaries. Upon hearing of the incident, the Egyptian Pharaoh intervened and negotiated with the Greeks—ultimately hiring them as mercenaries in his own service. A Greek mercenary settlement was established in Egypt, which eventually served as a gateway for economic and cultural exchange between the two civilizations.
Classical Greece, the Hellenistic Period, and the Roman Era
At the same time that Egyptian civilization was in its later stages, another ancient society was thriving in Mesopotamia. Among its most prominent centers was Babylon, a walled metropolis known for its sophisticated culture and bustling trade, attracting merchants from across regions. However, in the eastern reaches of Mesopotamia, a new power was rising—Persia. The Persian Empire expanded rapidly, conquering neighboring states one after another, including Babylon, and eventually forming a vast empire that challenged the balance of power in the region.
Meanwhile, Greece had grown into a network of independent city-states (poleis) along the eastern Mediterranean, but was not yet strong enough to rival Persia militarily. The Greeks, who were active seafarers in the Aegean Sea, eventually found themselves in open conflict with Persia in what became known as the Greco-Persian Wars. Against all odds, the loosely allied Greek city-states achieved an extraordinary victory over the mighty Persian Empire—a turning point in history.
This triumph marked the beginning of what we now call Classical Greece, a period during which Greek culture flourished. It was an era of immense creativity and intellectual achievement: literature, sculpture, architecture, and the foundations of what we now consider “classical” European culture all blossomed in this time.
Later, Alexander the Great, king of Macedon in northern Greece, launched a campaign to conquer Persia under the banner of avenging past conflicts. He succeeded in toppling the Persian Empire and building a new one that stretched from Greece to Egypt and deep into Asia. In Egypt, he founded the city of Alexandria, which would become a major center of learning and culture. However, Alexander’s sudden death led to the fragmentation of his empire.
In Egypt, one of Alexander’s generals, Ptolemy, took control and established the Ptolemaic Dynasty, a Greek-speaking royal house that ruled Egypt until it was absorbed by the Roman Empire. The period from Alexander’s conquests to the Roman annexation is known as the Hellenistic Period, which was followed by Roman rule in Egypt and the broader Mediterranean.
Classical Greek Thinkers and the Advanced Mathematics of Egypt
Until relatively recently, it was not widely known—or perhaps more accurately, it had been forgotten—that ancient Egypt had developed highly sophisticated mathematics. However, evidence now shows that the intellectual accomplishments of ancient Egyptian scholars were indeed substantial. During the Classical period of Greece, many Greek philosophers and statesmen acknowledged the advanced state of Egyptian knowledge. Numerous thinkers traveled to Egypt to study its science, philosophy, and governance.
The historian Herodotus, often called the “Father of History,” also visited Egypt. He was deeply impressed by its advanced culture and openly wrote that many aspects of Greek civilization—including religious beliefs—were influenced by what the Greeks had learned from Egypt.
Following the Roman conquest, Egypt later came under the influence of the Islamic world. In the early modern era, Egypt became subject to colonial powers from Europe. During this time, the rapid scientific and technological progress of Europe contributed to a worldview in which Europe was seen as “advanced,” while regions such as Egypt and much of Asia were often viewed as “backward.” As a result, the idea that ancient Egypt had once possessed advanced mathematics faded from common knowledge.
Characteristics of Egyptian, Babylonian, and Greek Mathematics
et’s now examine some of the distinct characteristics and differences between Egyptian, Babylonian, and Greek mathematics. For a long time, modern mathematics has been seen as having its roots in Greece. Greek mathematicians placed great importance on defining the assumptions behind their theories. That is, before engaging in any theoretical exploration, they clearly stated the axioms—statements accepted as self-evident truths—and then precisely defined the terms they would use. From there, they developed logical arguments based on a formal structure of reasoning, known as proof.
This approach—mathematics built on axioms, definitions, and proofs—is referred to as deductive mathematics, and it forms the foundation of modern mathematical thinking.
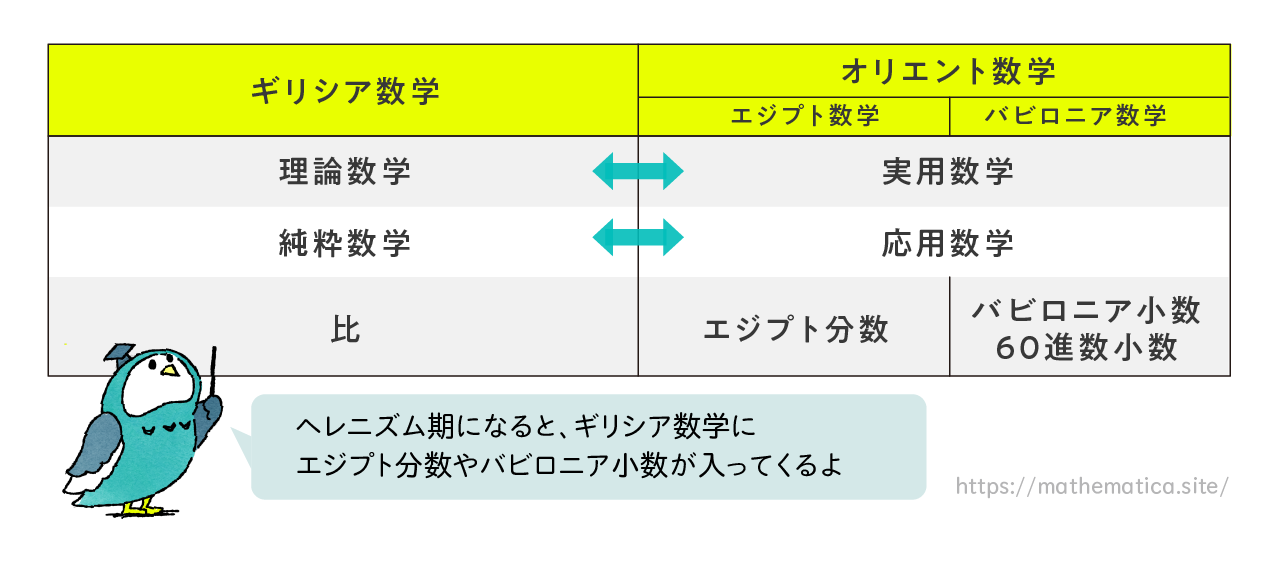
In contrast, the mathematical traditions of ancient Egypt and Babylonia, both part of the broader ancient Near Eastern or “Oriental” world, did not emphasize formal proof in the same way. These systems focused more on practical applications—solving concrete problems related to architecture, land measurement, trade, and astronomy. As a result, some critics have dismissed these traditions as merely utilitarian or as forms of technical craftsmanship lacking theoretical depth. However, this view has been increasingly challenged in recent scholarship.
In broad terms, we can say that Greek mathematics tended toward the theoretical, while Egyptian and Babylonian mathematics were more practically oriented. This distinction is sometimes framed as the difference between pure mathematics and applied mathematics.
Different Concepts of Numbers in Egypt, Babylonia, and Greece
Each of the three civilizations—Egyptian, Babylonian, and Greek—had its own unique way of understanding and using numbers.
In ancient Egypt, a special form of fractions known as Egyptian fractions was used. These represented all fractional values as sums of distinct unit fractions (like 1/2, 1/3, 1/4, etc.). We’ll explore this fascinating system in detail in a later article.
In Babylonia, a base-60 numeral system was used, including what are now called sexagesimal fractions (base-60 decimals). Interestingly, elements of this system still survive today in how we measure time and angles. For example:
23 degrees, 45 minutes, and 18 seconds =
23°45′18″ = 23 + 45/60 + 18/3600 = 23.755 degrees
In ancient Greece, mathematicians approached numbers differently. They developed a theory of ratios rather than treating fractions as numbers in themselves. It is important to note that, in classical Greek mathematics, a ratio (or proportion) was not considered a number.
For example, a statement such as “the ratio of my age to my brother’s is 3 to 5” was not expressed numerically as 3/5. Rather, it remained a relational concept that always involved a comparison between two quantities. In this context, four numbers were often involved (A : B = C : D), and the concept of a fraction as a standalone entity did not yet exist.
By contrast, in later mathematics, a ratio like 3:5 could be expressed as the fraction 3/5, which we now treat as a numerical object representing both a division and a specific value (0.6). In modern times, we often write ratios as a:b or a/b and treat them as abstract quantities. This shift in understanding occurred only after symbolic algebra became widely used, particularly during the early modern period.
So, to the Greeks, a ratio described the relationship between two magnitudes but was not itself an independent numerical object—unlike the modern concept of fractions.
How the Concept of Numbers Has Changed Over Time
In ancient Egypt, people used fractions—specifically, Egyptian unit fractions—as part of their number system. In Babylonia, people used sexagesimal decimals, a base-60 number system. These were considered valid forms of numbers within their respective cultures.
In contrast, the ancient Greeks understood numbers primarily as natural numbers. Other quantities—such as length, area, volume, and angles—were treated not as numbers, but as magnitudes, distinct from arithmetic numbers. For example, while many ancient civilizations would calculate the area of a rectangle as “length × width,” Greek mathematics generally did not adopt this formulaic approach in the same way.
This raises an interesting question: Why do we today calculate the area of a rectangle as “length × width”?
For us, this formula feels natural—but to a Greek mathematician, the concepts of “length,” “area,” and “multiplication” were not so easily or universally defined.
The Greek concept of number, particularly as developed in Euclid’s Elements, was grounded in the idea of whole numbers. Later, during the Hellenistic and Roman periods, we begin to see the influence of Egyptian fractions and Babylonian decimals appearing in Greek mathematical texts.
Famous mathematicians from the Hellenistic and Roman eras—such as Archimedes, Hero (Heron), and Ptolemy—made use of Egyptian fractions in their calculations. Archimedes even used both Egyptian and Babylonian numerical methods.
In practical life, even in Classical Greece, merchants, farmers, and engineers must have calculated areas of cloth, land, and structures using multiplicative methods—just as people in Egypt and Babylonia did. But for Greek mathematicians, defining abstract concepts such as “length,” “area,” or “multiplication” wasn’t a necessary part of their theoretical framework. Greek mathematics was rooted in pure reasoning, not practical computation.
Today, we might define “length” as a positive real number, but it’s worth noting that the formal definition of real numbers wasn’t established until the 19th century. Defining fundamental concepts such as number, length, or area in rigorous mathematical terms has turned out to be far more difficult than one might expect.
In summary, the idea of “number” is not universal—it has evolved across time and cultures.
Egyptian, Babylonian, and Greek mathematicians all had different approaches to numerical thinking.
Even the numbers we now take for granted—like the ratio of a circle’s circumference to its diameter (π ≈ 3.1415…) or the golden ratio (φ ≈ 1.618…)—were not part of the worldview of people in ancient or Renaissance times.
The Enigma of Pi: What Does the “True Value” Really Mean?
We’ve been exploring the concept of pi (π), and it is well known that Archimedes calculated an approximation of π as 22/7. Importantly, he understood that this was not the true value of pi, but rather a close estimate. He likely knew that even more accurate approximations were possible.
But here’s a philosophical question:
Did Archimedes ever wonder, “What is the true value of pi?”
Let’s pause for a moment. When you pick up a pencil, do you ask, “What is the true length of this pencil?” In everyday life, we don’t usually think in such terms. In fact, if we measure something to ten decimal places, the level of precision may already exceed the size of atoms. The actual value of π is defined as the result of an infinite calculation. The idea of striving to know pi’s true, infinite value did not arise until much later in the history of mathematics.
Human beings tend not to pursue what they do not need. It is only as mathematics became more abstract and analytically powerful that the notion of determining the “true value” of π began to matter.
In this series, when we talk about pi and the golden ratio φ, we are referring not to their exact irrational values, but to the approximate values used historically. This distinction becomes important in contexts such as the mysteries surrounding the Great Pyramid.
For example, one famous claim is:
If you divide the perimeter of the Great Pyramid’s base by twice its height,
you get the value of pi.
But both the perimeter and the height of the pyramid are measured values, and as such, any resulting calculation is an approximation. Therefore, if we treat pi as its exact, irrational value, then no amount of precise measurement could ever truly “prove” this connection. That might seem like a minor technicality—but it’s an important one to clarify.

