A prime number is a natural number that has no positive divisors other than 1 and itself.
The smallest prime number is 2, which is also the only even prime number.
For example, the prime numbers between 1 and 100 include:
2, 3, 5, 7, 11, 13, 17, 19, …
There are a total of 25 prime numbers in this range.
The Concept of Prime Numbers in Ancient Greece
In ancient Greek mathematics, numbers were categorized based on how they could be arranged using pebbles. For example:
- Numbers that could be arranged evenly into two rows were considered “even numbers.”
- Numbers that left one pebble when arranged in two rows were “odd numbers.”
In this way, the Greeks developed mathematical concepts by associating numbers with geometric shapes. This practice laid the foundation for theoretical reasoning at the time.
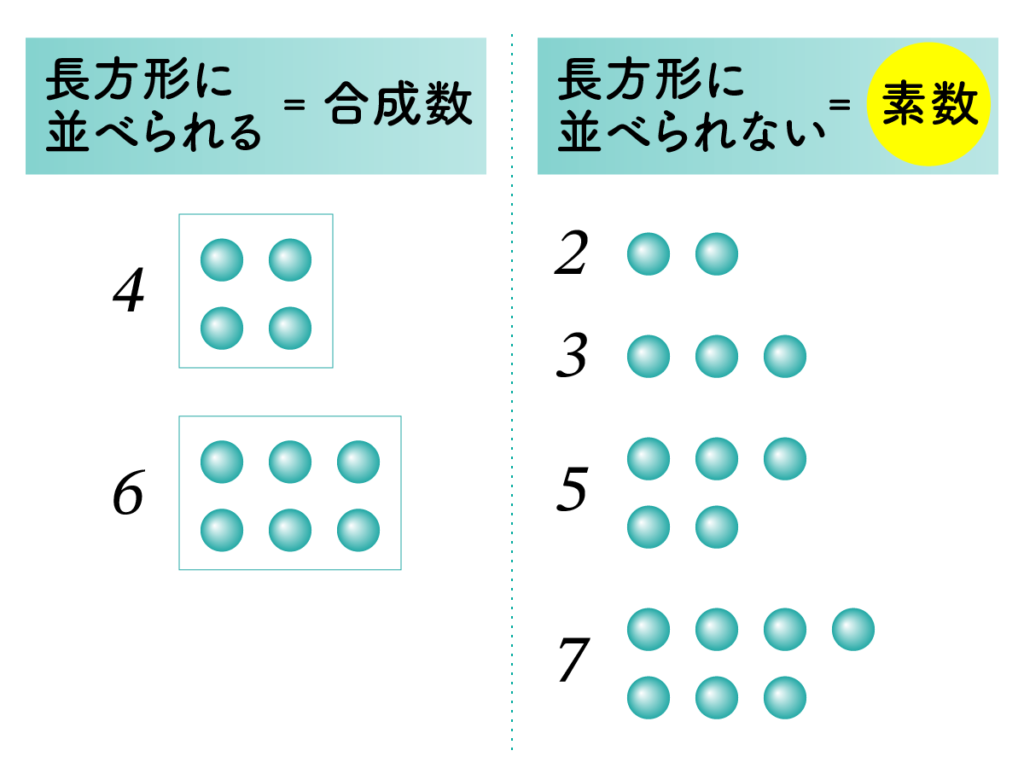
Classifying Numbers Based on Rectangular Arrangement
The ancient Greeks placed great importance on whether a number could be arranged in the shape of a rectangle.
Numbers like 4, 6, and 9, which can be arranged into two or more rows and columns, were called rectangular numbers (excluding single-row arrangements). In modern terms, these correspond to composite numbers.
In contrast, numbers that could not be arranged into a rectangle — that is, those that formed neither squares nor rectangles — were considered prime numbers by the Greeks.
Examples:
Numbers like 2, 3, 5, and 7 cannot be arranged into any rectangular shape using pebbles, and were thus recognized as prime numbers.
How the Ancient Greeks Classified Numbers by Shape
In ancient Greece, numbers were categorized based on the shapes they could form when arranged with small pebbles.
For example:
- Numbers that can be neatly arranged into two equal rows were called even numbers.
- Numbers that leave one pebble out when arranged into two rows were called odd numbers.
In this way, the visual or geometric appearance of numbers served as a basis for classification, and creating new terms (i.e., concepts) from these shapes marked the beginning of mathematical theory in ancient times.
What Is Prime Factorization?
Among natural numbers, any number that is not a prime number (i.e., a composite number) can be expressed as a product of two or more prime numbers. This process of breaking a number down into a product of prime numbers is called prime factorization.
The Relationship Between Composite Numbers and Rectangular Numbers
A composite number is a natural number greater than 1 that can be expressed as the product of two or more natural numbers.
For example, if a composite number a can be written as the product of b and c, then placing pebbles in b rows and c columns will form a rectangle.
This idea—thinking of composite numbers as quantities that can be arranged into rectangles—was characteristic of ancient Greek thinking. They referred to composite numbers as rectangular numbers.
If either b or c is also a composite number, it can be further broken down into smaller factors. Repeating this process eventually leads to a product of prime numbers.
These primes, which are factors of the composite number, are called prime factors. The process of expressing a number as a product of its prime factors is known as prime factorization.
Why Were the Ancient Greeks Fascinated by Prime Numbers?
The ancient Greeks—and ancient peoples in general—believed that numbers held mystical meaning and power in themselves. For example, a composite number a = b × c was not just a product, but a combination of the “meanings” or “powers” of b and c.
In the same way:
- A square number a² was seen as the power of a “doubled,”
- A cube number a³ as carrying “triple” the power.
In this line of thinking, prime numbers, which cannot be broken down into a product of other numbers, were seen as something truly special.
They existed independently of other numbers, with a pure and unique essence—irreducible, original numbers that carried a profound sense of mystery.
A Beautiful Proof: The Infinitude of Prime Numbers
“The number of primes is infinite”—
This fact was demonstrated by the ancient Greek mathematician Euclid in his famous work Elements,
and has since been praised by generations of mathematicians as one of the most beautiful proofs in history.
証明の流れ
まず、「素数は有限個しか存在しない」と仮定してみます。
すべての素数を並べたとき、それが
p₁, p₂, p₃, …, pₖ
の k個しか存在しないとしましょう。
このとき、次のような新たな数を考えます：
a = p₁ × p₂ × p₃ × … × pₖ + 1
この a は、すでにあるすべての素数 pi で割ると「1余る」ため、どの素数でも割り切れません。
したがって：
- a が素数なら、それは 新しい素数です（もとのリストに含まれていない）→ 矛盾！
- a が合成数なら、その約数には必ず素数が含まれますが、それもやはりリストにない → 矛盾！
このように、「素数は有限個しかない」と仮定すると矛盾が生じます。
ゆえに、素数は無限に存在することが論理的に導かれるのです。
The Sieve of Eratosthenes
The “Sieve of Eratosthenes” is a method for efficiently identifying all the prime numbers within a certain range. It is a simple yet powerful algorithm that remains widely used today—from elementary school students to professional mathematicians. The name of this method comes from the ancient Greek scholar, Eratosthenes.
Eratosthenes was a prominent intellectual figure of the Hellenistic era, a great ancient Greek scientist who made contributions across many fields including mathematics, astronomy, and geography.
He is especially well-known for being the first person to measure the circumference of the Earth.
Summary
Prime numbers are natural numbers that have no divisors other than 1 and themselves, forming a conceptual pair with composite numbers.
In ancient Greece, numbers were imbued with form and meaning, and prime numbers in particular were considered to hold mystical significance.
Euclid famously proved the infinitude of primes through elegant logic—an insight that has echoed through history to the present day.
The “Sieve of Eratosthenes” is a classical algorithm that efficiently identifies many primes through a simple process.
Primes are more than mere numbers—they are special entities at the intersection of theory, history, and philosophy.
And the pursuit of their secrets continues even today.