The Most Beautiful Ratio — The Golden Ratio
Often called “the most beautiful ratio,” the golden ratio is a mysterious number that appears not only in ancient Greek mathematics but also in modern design and throughout the natural world.
This article offers a clear and engaging introduction to the golden ratio—starting with its definition and how to calculate it, exploring its connection to the Fibonacci sequence, its appearance in structures like pentagrams and pyramids, and even its patterns in nature.
Let’s explore the “mathematics of beauty” hidden all around us.
What Is the Golden Ratio?
The golden ratio is considered one of the most aesthetically pleasing proportions to the human eye. It has been widely used in works of art, architecture, and commercial design. Chances are, you’ve heard the term “golden ratio” at least once.
But what exactly is this “golden ratio”? What does it represent in mathematical terms?
Definition and Calculation of the Golden Ratio
As shown in Figure 1, let’s divide a line segment AB at a point C. Let AC be the shorter part, denoted as a, and CB be the longer part, denoted as b.
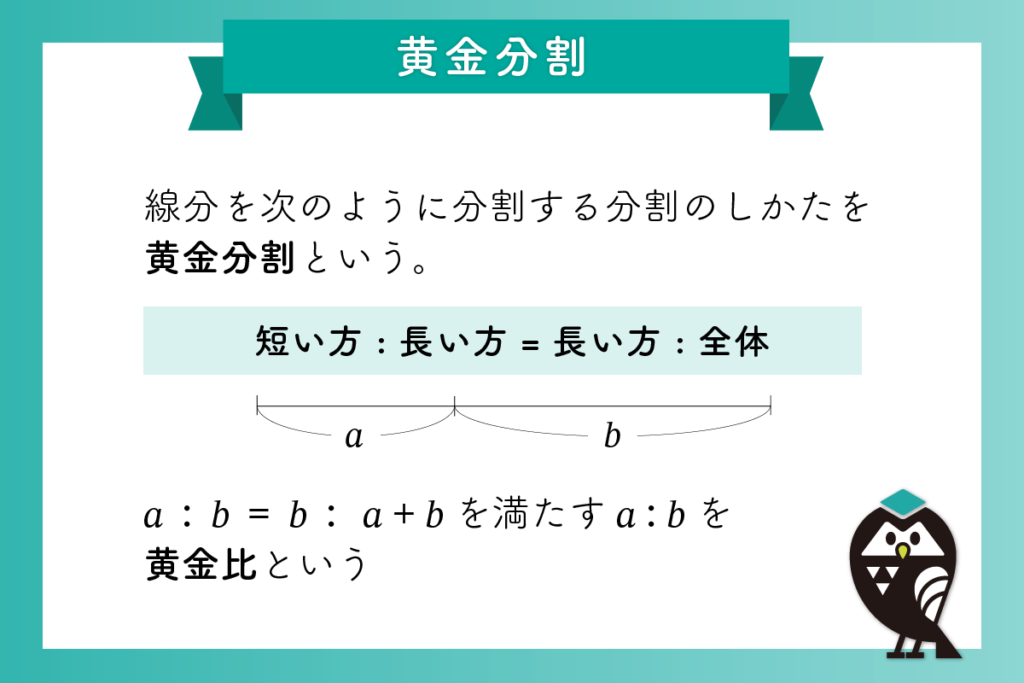
When the segment is divided in such a way that the following proportion is satisfied, the division is called a golden section:
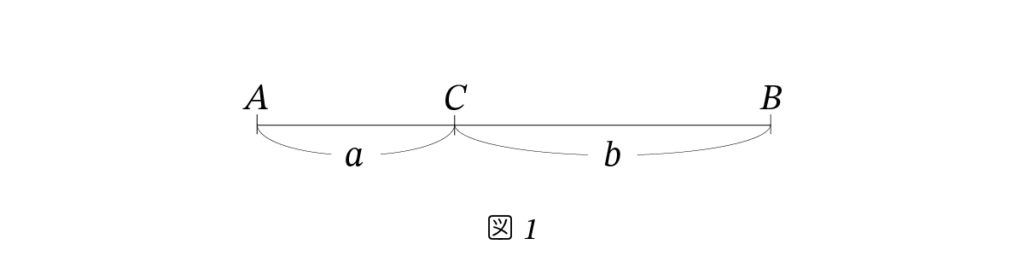
The shorter part : the longer part = the longer part : the whole
This relationship can be written as:
a : b = b : (a + b) (1)
A ratio that satisfies this condition—b/a or a/b—is called the golden ratio, and its value (approximately 1.618…) is often referred to as the golden number or golden mean.
This ratio is commonly denoted by the Greek letter φ (phi) and is famously found in natural structures, classical architecture, and the geometry of the pentagram.
Calculating the Golden Ratio
By applying the concept of cross-multiplication to the previously mentioned proportion (1), we arrive at the following equation:
b² = a × (a + b) (2)
Dividing both sides of equation (2) by a² and letting x = b / a, we obtain the following quadratic equation:
x² = 1 + x (3)
Solving this equation for the positive root gives:
φ = (1 + √5) / 2 ≈ 1.6180339887… (4)
This value, φ (phi), is known as the golden number, and the ratio 1 : φ is referred to as the golden ratio.
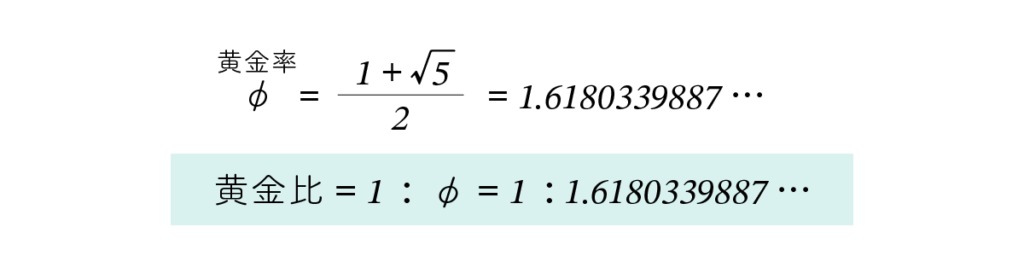
The Relationship Between the Golden Ratio and the Fibonacci Sequence
The golden ratio, φ (phi), is known as a beautiful proportion that appears even in nature.Interestingly, this mysterious ratio has a deep connection with the Fibonacci sequence.
What Is the Fibonacci Sequence?
The Fibonacci sequence is a series of numbers that goes as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Let’s calculate the ratio of each pair of consecutive numbers (later number ÷ previous number) in the sequence:
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 ≒ 1.666…
8/5 = 1.6
13/8 ≒ 1.625
21/13 ≒ 1.615…
34/21 ≒ 1.619…
As we can see, the ratio of consecutive Fibonacci numbers gradually approaches φ (1.6180339887…).
In fact, the ratio between adjacent terms in the Fibonacci sequence is known to converge to the golden ratio.
This property is said to be connected to many natural phenomena, such as the arrangement of leaves on plants, the spirals of seashells, and the shapes of galaxies.
What Was the Concept of “Ratio” in Greek Mathematics?
One of the defining features of ancient Greek mathematics was its emphasis on the concept of ratio.
Among these, the golden ratio—known in ancient times as the division in extreme and mean ratio—was of particular interest and significance.
Did Greek Geometry Avoid Using Numbers?
In Greek mathematics—particularly in geometry—constructions were carried out using only a straightedge and compass. Theoretical developments were based not on numerical calculations, but on geometric constructions and relationships.
This was not because numbers were forbidden, but rather because numerical values were not assumed to exist as a starting point for mathematical reasoning.
Greek geometry began with clearly defined definitions and axioms—concepts allowed within the system—and built its arguments through strict logical progression.
This approach became the foundation for mathematical reasoning in Western tradition and has been carried on ever since.
A Ratio Is a Relationship, Not a Number
For the ancient Greeks, a ratio a : b did not represent a numerical value like b ÷ a, as we understand it today. Instead, it expressed a relationship between two quantities, a and b.
Moreover, irrational numbers such as φ (phi) = 1.618… were not recognized as “numbers” in the Greek sense.
The concept of irrational numbers being treated as actual numerical values came much later, during the modern era.
So How Was the Golden Ratio Treated in Ancient Times?
In ancient times, when numerical values like the golden ratio (1.618…) could not be used directly, the golden ratio was understood as a geometric relationship rather than a number.
For example, the lengths of certain line segments within a pentagram (five-pointed star) naturally embody the golden ratio.
In Greek geometry, the beauty and structure of the golden ratio were grasped through proportional relationships found within geometric figures.
Let’s now take a closer look at the pentagram, a shape that frequently appears in Greek geometry.
The Pentagram and the Golden Ratio
The Hidden Beauty of Proportion in a Geometric Figure
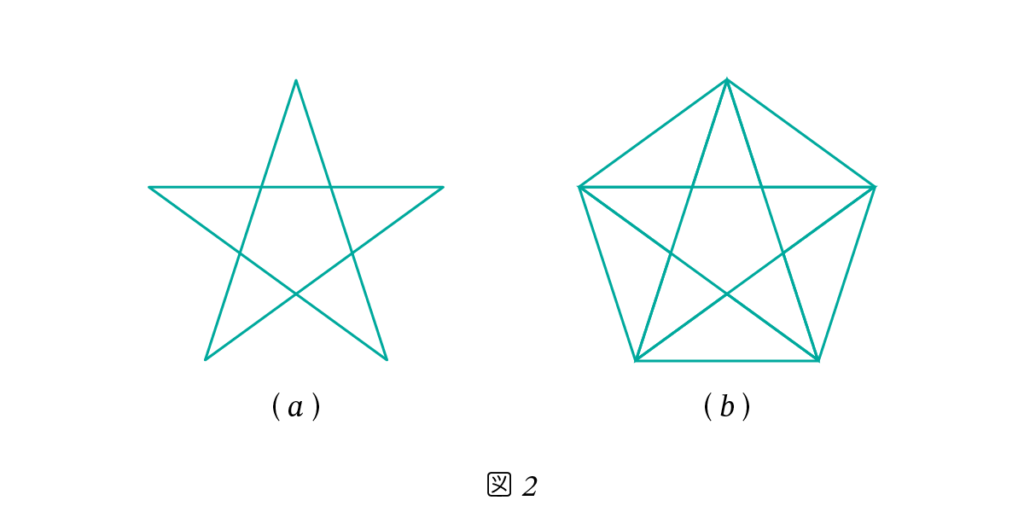
The star-shaped figure shown in Figure 2-(a) is called a pentagram.
In ancient Greece, the pentagram held special significance for the Pythagorean school and was revered as a sacred symbol of their teachings.
Within the pentagram, the golden ratio appears repeatedly.
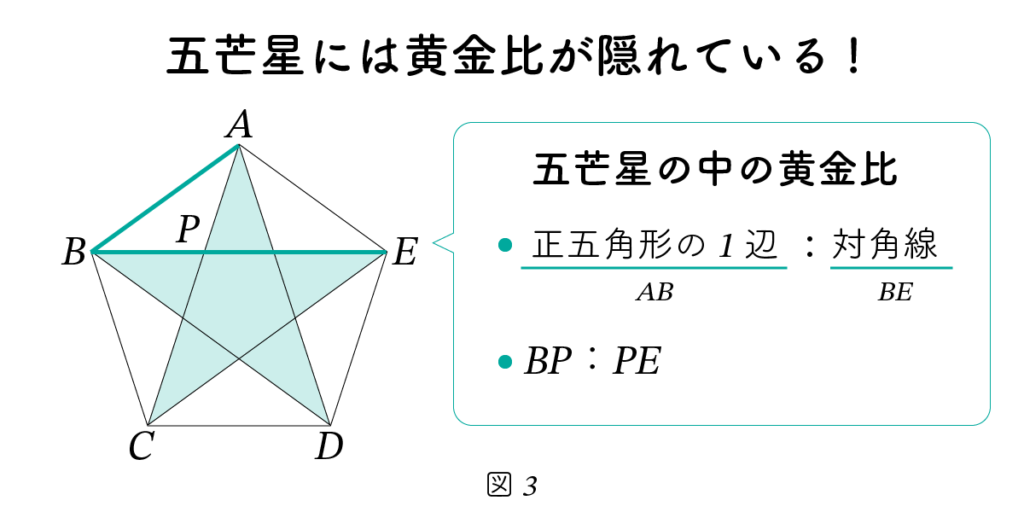
For example, when the tips of the star are connected by lines, a regular pentagon emerges in the center, as shown in Figure 2-(b).
Within this regular pentagon, the golden ratio can be found hidden in various proportions and structural relationships.
One of the most well-known examples is the ratio AB : BE shown in Figure 3—
that is, the ratio of a side to a diagonal in a regular pentagon.
This proportion is a classic instance of the golden ratio appearing in geometric form.
The Golden Ratio in Nature
The golden ratio appears not only in geometric figures, but also throughout the natural world.
You can observe this proportion in the arrangement of leaves on a stem, the spirals of seashells, and the patterns of flower petals.
The presence of the golden ratio in nature has long been seen as supporting the Pythagorean idea that “nature is governed by numerical ratios.”
The Golden Rectangle — A Beautiful, Recurring Structure
Some geometric figures have the property of containing smaller versions of themselves within their own shape.
This kind of structure is known as a recursive structure, and a prime example of it is the golden rectangle.
What Is a Golden Rectangle?
A golden rectangle is a rectangle whose side lengths are in the golden ratio (a : b).
If you remove a square with side length a from the golden rectangle, the remaining portion will also be a golden rectangle.
This process can be repeated infinitely, creating a recursive structure made up of an endless series of squares.
Figure 4 shows an example of such a golden rectangle formed through this method.
Golden Rectangle Structures Found in Nature
This recursive structure can actually be observed in nature—for example, in the spirals of seashells.
The presence of mathematical forms like the golden ratio within the beauty of the natural world offers us both wonder and inspiration.
Is the Golden Ratio Hidden in the Pyramids?
The Great Pyramid of Egypt is counted among the Seven Wonders of the Ancient World and has fascinated people for centuries.
One of the most frequently discussed mysteries surrounding it is the idea that the golden ratio is hidden within its design.
Does the Ratio of Base Area to Face Area Reflect the Golden Ratio?
According to this theory, the ratio between the base area (S₁) and the face area (S₂) of the Great Pyramid matches the golden ratio φ (phi) = 1.6180339887…
Expressed as a formula:
S1 / S2 = φ = 1.6180339887 …
…is said to hold true. And when we actually perform the calculation, we find that the ratio does indeed come very close to the golden ratio.
But is this just a coincidence?
Or did the ancient Egyptians intentionally incorporate this ratio into the design of the pyramid?
In the web series “The Hidden Secrets of the Pyramid,” we explore the mystery of the golden ratio from various angles—through the lens of ancient Egyptian history, mythology, and mathematical knowledge.
If you’re interested, be sure to check it out ▼
Summary
The golden ratio is more than just a number—it is a special proportion that lies at the intersection of mathematics, nature, and beauty.
Derived from the relationship
short side : long side = long side : whole,
it is expressed by the formula
φ = (1 + √5) ÷ 2 ≈ 1.618.
The ratio of consecutive terms in the Fibonacci sequence converges toward this value.
The golden ratio appears in geometric figures like the pentagram and the golden rectangle, in seashells and plant arrangements, and is even said to be found in the design of the Egyptian pyramids.
It is a proportion that has fascinated ancient philosophers and continues to inspire modern artists and scientists alike.
The golden ratio may offer a clue to answering one of the deepest questions of all:
Why do we perceive something as beautiful?

