Do you know what types of regular polyhedra exist? In this article, we provide a clear and accessible explanation of the “Platonic solids,” which play an important role in both mathematics and the natural world.
Plato and Geometry: “God Always Geometrizes” — Where Philosophy Meets Mathematics
The ancient Greek philosopher Plato was so influential that later thinkers famously claimed, “All of philosophy is a footnote to Plato.”
He placed great importance on mathematical education and left behind many profound quotes.
For example, his belief that “learning should be pursued for the sake of knowledge itself, not for profit or practical use” still resonates today.
Plato also embraced a form of mysticism, believing that universal truths were hidden within numbers and geometric forms.
One of the most iconic expressions of this belief is the famous phrase:
“God always geometrizes.”
This saying illustrates how deeply Plato regarded geometry as something sacred.
Why Are There Only Five Platonic Solids in the World?
Let us introduce the Platonic solids, also known as the cosmic solids.
In mathematics, these solids are simply called regular polyhedra.
A regular polyhedron is a three-dimensional shape that satisfies the following two conditions:
- All faces are identical regular polygons.
- The same number of faces meet at every vertex.
The second condition is important because it excludes shapes like two tetrahedra glued together, which might otherwise seem regular.
Although it might seem that you could create as many regular polyhedra as you like by increasing the number of faces, in reality, only five such shapes exist that meet these strict conditions.
These five shapes, shown below, are what we call the Platonic solids — unique and profound figures in both mathematics and philosophy.
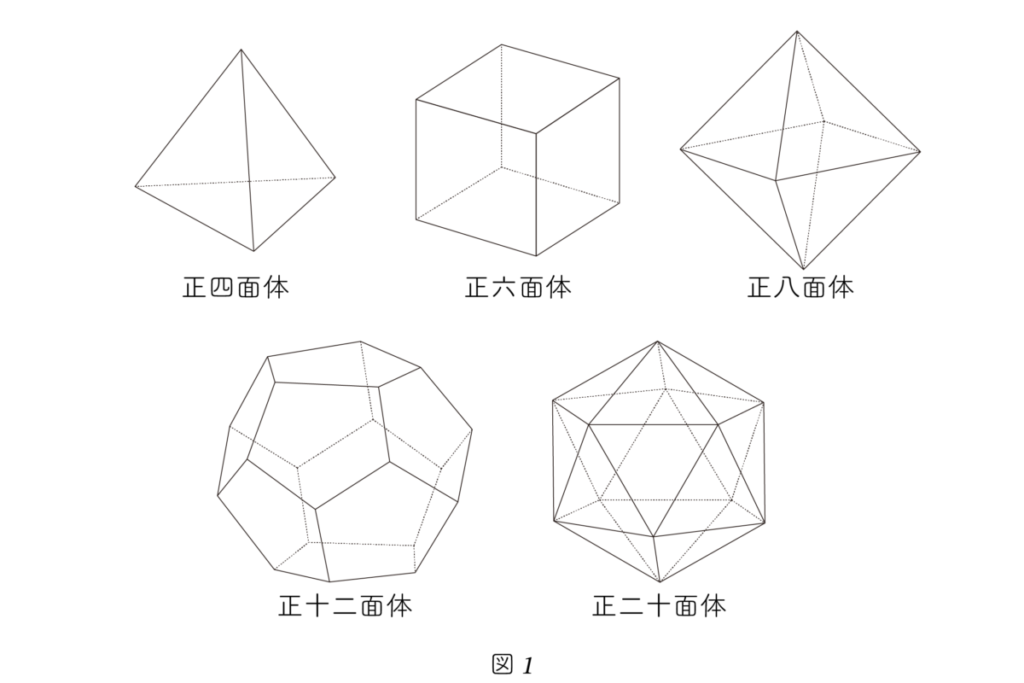
Why Are There Only Five Regular Polyhedra?
The reason why there are only five regular polyhedra is actually not that complicated.
The key lies in how many regular polygons can meet at a single vertex.
Let’s begin with equilateral triangles.
- If three equilateral triangles meet at one point, they form a tetrahedron.
- If four triangles meet, they form a pyramid with a square base, and joining two of these gives an octahedron.
- If five triangles meet, they form part of an icosahedron.
In other words, there are three types of regular polyhedra that can be built using equilateral triangles.
The interior angle of an equilateral triangle is 60°.
When six such triangles meet at a point, the angle sum is 60 × 6 = 360°, which lies flat and cannot form a solid shape.
Let’s examine other regular polygons:
- A square has an interior angle of 90°. Three squares meeting at a point give 270°, and four give 360°. → A cube (hexahedron) can be built with three, but beyond that, the shape becomes flat.
- A regular pentagon has an interior angle of 108°. Three pentagons make 324°, which is still less than 360°. → A dodecahedron is possible.
- A regular hexagon has an interior angle of 120°. Three hexagons give exactly 360°, so again, no solid shape can form.
As the number of sides increases, the interior angles also increase, and just three such polygons will already exceed 360°.
Therefore, no regular polyhedron can be formed using regular polygons with six or more sides.
This is why there are exactly five regular polyhedra, as shown in Figure 1.
Plato believed that regular polyhedra could be further broken down into two specific types of right triangles.
These are:
- The right triangle formed by dividing an equilateral triangle in half, and
- The isosceles right triangle.
Plato referred to these two triangles as stoicheia — the elemental triangles.
Interestingly, the triangular rulers we use today in stationery sets are also based on these two shapes.
The Greek word “stoicheia” (στοιχεῖα) means “element,” “foundation,” or “basic unit.”
This term was later used as the title of the famous mathematical work Elements by the mathematician Euclid.
Plato stated the following:
“God gave these two basic triangles (stoicheia) as the primary elements (archai) of the four natural elements.”
Here, the stoicheia refers to:
- The isosceles right triangle
- The right triangle formed by halving an equilateral triangle
According to Plato’s theory, all regular polyhedra are constructed from these fundamental triangles.
For example:
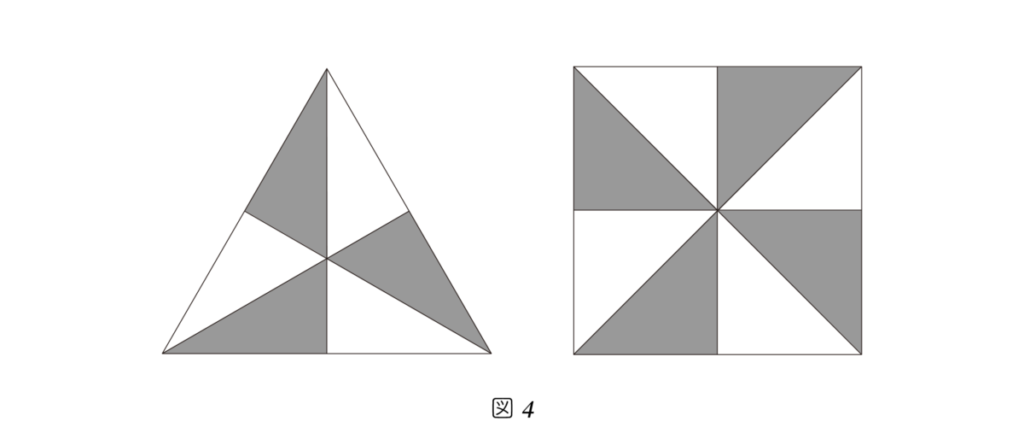
- An equilateral triangle is made up of six elemental triangles (see Figure 4).
- A square consists of eight elemental triangles.
Based on this, we can calculate the total number of elemental triangles that make up each regular polyhedron as follows.
| Regular Polyhedron | Number of Faces | Elemental Triangles per Face | Total |
|---|---|---|---|
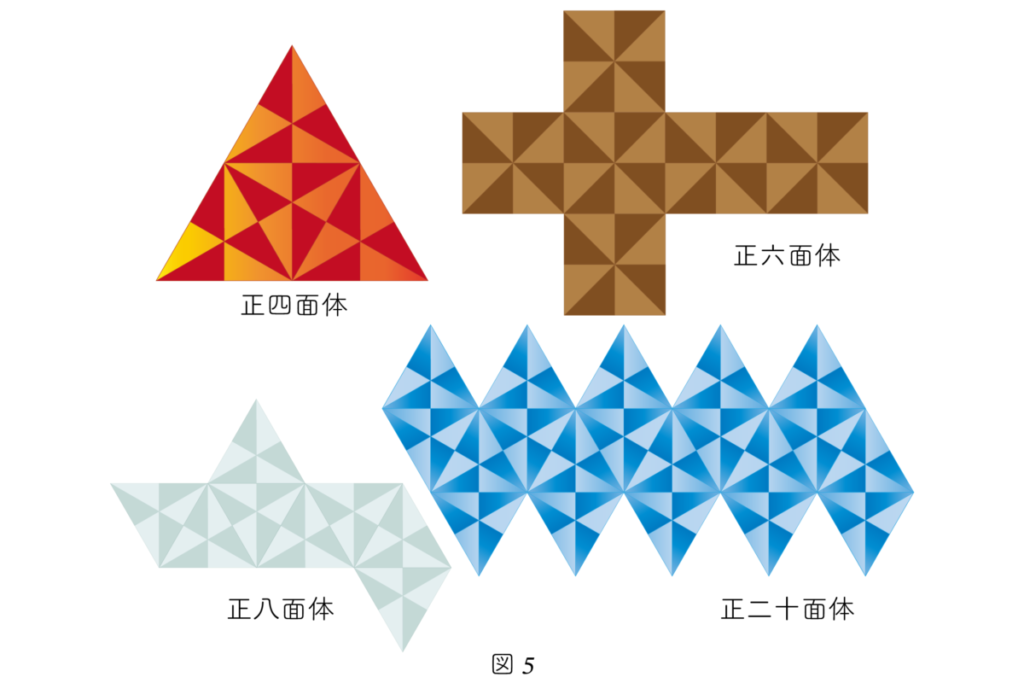
| Tetrahedron | 4 faces | 6 triangles | 24 |
| Octahedron | 8 faces | 6 triangles | 48 |
| Icosahedron | 20 faces | 6 triangles | 120 |
Thus, Plato believed that the regular polyhedra were meticulously constructed from the “elemental triangles” bestowed by the gods.
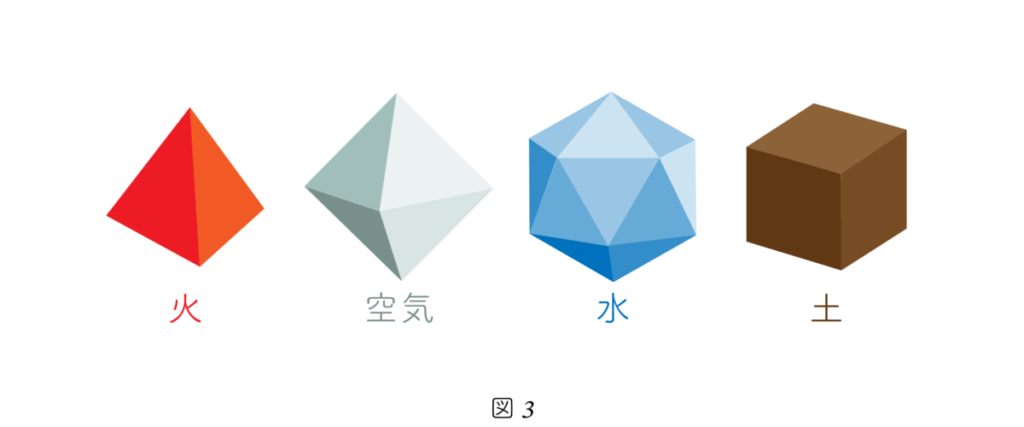
The Meaning Behind the Assignment of Regular Polyhedra to the Four Elements: Plato’s Cosmic Vision
When Plato assigned the five regular polyhedra to the four classical elements,
he based each correspondence on the shape and properties of the solids:
- The tetrahedron has sharp angles and a pointed form, thus it represents fire.
- The cube (hexahedron) has square faces and a stable structure that can tessellate a plane, making it suitable for earth.
- The icosahedron is the roundest and most sphere-like of the five, symbolizing water.
Additionally, both fire (tetrahedron) and water (icosahedron) are composed of triangular faces,
and the octahedron, which lies between them in terms of shape, represents air.
In Plato’s thought:
- Water turns into air through evaporation
- Fire is lighter than air (i.e., it has the smallest form)
In this way, each regular polyhedron was matched with a natural element,
and Plato developed a cosmology where the structure of the universe could be explained through geometry.
The “Fifth Element” That Fills the Cosmos — The Dodecahedron and the Mystery of Aether
So what does the remaining shape—the dodecahedron—represent?
The dodecahedron is a beautiful solid composed entirely of regular pentagonal faces.
Plato associated this shape with “that which envelops the whole universe,” in other words, aether, the fifth element.
He was strongly influenced by the Pythagorean school, inheriting from them ideas such as numerical mysticism—the belief that numbers hold divine meaning—and the doctrine of reincarnation of the soul.
The regular pentagon itself contains the pentagram, a sacred symbol deeply valued by the Pythagoreans.
When each vertex of a regular pentagon is connected to its non-adjacent vertices with diagonals, another pentagon emerges in the center.
By continuing this process in a single stroke along the diagonals, a five-pointed star, or pentagram, appears.
This star is called a pentagram, and it served as the symbol of the Pythagorean brotherhood.
Moreover, if you draw a perpendicular from each vertex of the pentagon to its opposite side,
the interior of the pentagon can be divided into 30 right triangles (see Figure 6).
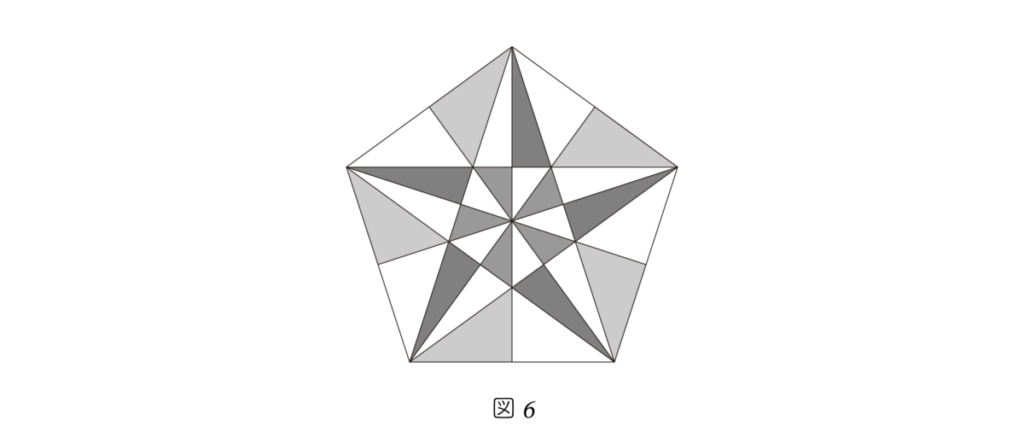
The breakdown is as follows:
- 10 right triangles appear within the small central pentagon
- 10 right triangles form the “arms” of the pentagram
- 10 right triangles are located in the outer regions of the pentagram
Together, this creates a total of 30 right triangles within a single regular pentagon.
If these 30 right triangles are distributed across the 12 faces of a dodecahedron,
then the entire shape consists of:
30 × 12 = 360 right triangles
Plato regarded the dodecahedron as the “vessel of the cosmos,” embracing all things.
The symbolic meaning of the numbers contained within this structure also reflects the deep influence of Pythagorean philosophy:
- 30 represents the number of days in a month
- 12 corresponds to the number of months in a year
- 6 and 10 were considered sacred numbers by the Pythagoreans
Thus, the dodecahedron as a symbol of the universe embodies not only geometric beauty,
but also numerical symbolism and philosophical meaning.
Later on, the dodecahedron came to be associated with the mysterious “fifth element” that filled the entire universe—aether.
This concept of aether was actually widely believed by scientists until as recently as the 19th century.
The reason was that if light or gravity were to be considered waves, then there had to be some medium through which those waves could travel.
Just as ocean waves require water, and sound waves require air,
it was believed that something must carry waves through space—and that “something” was thought to be aether.
The Geometric Beauty That Enchanted Da Vinci: Platonic Solids and The Divine Proportion
The Platonic solids continued to be referenced by many throughout history.
During the Renaissance—a period marked by renewed interest in Greek and Roman culture—these shapes gained particular attention.
One of the most famous artists of this era, Leonardo da Vinci, was also an exceptional illustrator.
His friend, Luca Pacioli, a Franciscan friar, was not only known for promoting double-entry bookkeeping, but also believed that mathematics was a part of theology. He authored a book titled The Divine Proportion.
In this book, da Vinci illustrated the Platonic solids.
His drawings were so precise that it is said he may have constructed physical models to render them accurately.
There were even claims that someone once possessed one of these models, though it was likely not one made by da Vinci himself.
The Platonic solids have continued to be admired and referenced by many through the ages.
Among all periods, it was during the Renaissance—a time when ancient Greek and Roman culture was being rediscovered and reappraised—that the beauty and symbolism of Platonic solids attracted particular attention.
A prominent figure of this era was Leonardo da Vinci.
He was not only a masterful painter but also an exceptional illustrator.
One of da Vinci’s close friends was Luca Pacioli, a Franciscan friar.
Pacioli is known for popularizing double-entry bookkeeping, but he was also a thinker who regarded mathematics as part of theology.
In his influential work De Divina Proportione (The Divine Proportion), Pacioli explored mathematical ratios and their connection to divine harmony.
The illustrations in this book were provided by Leonardo da Vinci himself.
He drew several polyhedra, including the Platonic solids, and his drawings were highly praised for their precision and elegance.
So exact were his illustrations that some believed he must have constructed physical models before drawing them.
In fact, there were even claims by individuals who said they had seen models built by da Vinci,
though these were likely later reproductions and not originals made by Leonardo himself.
Kepler’s Cosmic Dream — The Secrets of the Planets Explained by Platonic Solids
Later, Europe entered the era of the Scientific Revolution, a time when great scientists like Newton and Kepler came to the forefront.
One of them, Johannes Kepler, also held a mystical view of the universe.
He believed, “This universe must have been created by God using geometry.”
At that time, the known planets were six: Mercury, Venus, Earth, Mars, Jupiter, and Saturn.
Kepler began to wonder:
“Why are there exactly six planets? Could this be related to the fact that there are only five Platonic solids?”
Astronomers of the era were well-versed in Euclidean geometry, inherited from ancient Greece.
That body of knowledge included theory concerning spheres inscribed and circumscribed within regular polyhedra.
Kepler’s Model Based on Platonic Solids
Building on this theory, Kepler proposed the following model:
- The innermost sphere represented Mercury’s orbit
- Surrounding that, a regular octahedron
- Then a sphere representing Venus’s orbit
- Around that, a regular icosahedron
- Then came Earth → regular dodecahedron → Mars → regular tetrahedron → Jupiter → regular hexahedron → Saturn
In other words, he envisioned the planetary orbits as nested spheres, each inscribed or circumscribed around a Platonic solid, stacked one after another.
Surprisingly, the model’s calculated values closely matched the astronomical data available at the time.
However, in later years, Kepler himself discovered a crucial fact:
Planetary orbits are not perfect circles, but ellipses—
a truth that directly contradicted the foundation of his geometric model.
Yet Kepler remained undeterred. He continued to embrace this “Universe = Platonic Solids” theory with pride throughout his life.
In this way, Platonic solids continued to captivate scientists from antiquity through the Renaissance.
Conclusion: The Shape of the Cosmos in Geometry – Reflections on the Platonic Solids
The ancient Greek philosopher Plato believed that the geometric beauty and order of the regular polyhedra held the truths of the cosmos within them.
He focused on the five perfectly symmetrical solids—the Platonic solids—each of which was assigned to one of the four classical elements: fire, air, water, and earth. The most mysterious of them all, the dodecahedron, was said to symbolize the aether, the substance that filled the universe.
To Plato, these shapes were not just mathematical figures. They embodied a profound philosophical system, rich in numerical mysticism and symbolic correspondences with nature—a worldview that deeply influenced the Pythagoreans, later philosophers, and scientists.
During the Renaissance, Leonardo da Vinci captured their elegance in his meticulously illustrated drawings, while Kepler attempted to explain the structure of the solar system using Platonic solids.
Thus, the Platonic solids have continued to serve as powerful symbols, linking God and nature, philosophy and mathematics, the cosmos and human thought—inspiring imagination and inquiry from antiquity to the modern day.

