— A Mysterious Sequence Found in Nature —
The Fibonacci sequence is a fascinating series of numbers that appears even in nature.
From the number of flower petals to the spirals of seashells and the reproduction patterns of rabbits—
these seemingly unrelated phenomena all share an underlying mathematical pattern.
In this article, we’ll clearly explain what the Fibonacci sequence is, its mathematical rules, its connections to the natural world, and how it relates to the golden ratio, a concept well known in the history of mathematics.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Have you noticed a pattern in this sequence of numbers?
This is the famous Fibonacci sequence, which follows a simple rule: each number is the sum of the two preceding ones.
The Fibonacci sequence is well known not only in mathematics but also for its appearance in nature and art. It often shows up in middle and high school math classes, as well as in entrance exams.
Let’s take a closer look at this sequence, filled with both the beauty and mystery of numbers.
What Is the Rule Behind the Fibonacci Sequence?
The Fibonacci sequence is a series of numbers arranged as follows:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
This sequence follows a simple rule:
each number is the sum of the two preceding numbers.
For example:
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
…
By continuing this rule, the sequence grows naturally.
It’s a mysterious and beautiful sequence that also appears in nature and art around us.

The Origin of the Name “Fibonacci Sequence”
— Who Was Leonardo of Pisa?
The name Fibonacci sequence comes from the medieval Italian mathematician Fibonacci, also known as Leonardo of Pisa.
As a young man, Fibonacci traveled to the eastern Mediterranean region due to his father’s work as a merchant. There, he studied Arabic mathematics, which was at the forefront of mathematical knowledge at the time.
Around the year 1200, he returned to Pisa and published a book compiling what he had learned.
In that book appeared the sequence that would later become known as the Fibonacci sequence. The original problem is said to have originated from a Sanskrit poem in ancient India.
However, the sequence did not gain widespread attention until much later.
It wasn’t until the 19th century that the French mathematician Édouard Lucas gave the sequence its modern name, Fibonacci sequence, and brought it into the realm of serious mathematical study.
The Rabbit Problem: How Many Pairs After One Year?
In his book, Fibonacci introduced the famous sequence through the following story:
One day, a farmer receives a single pair of baby rabbits (one male and one female).
These rabbits follow these rules:
- A baby rabbit becomes an adult after one month.
- From the second month onward, each adult pair produces one new pair of rabbits every month.
- Each newly born pair also begins reproducing after one month.
Given these conditions, if the farmer starts raising rabbits with just one pair,
how many pairs of rabbits will there be after one year?
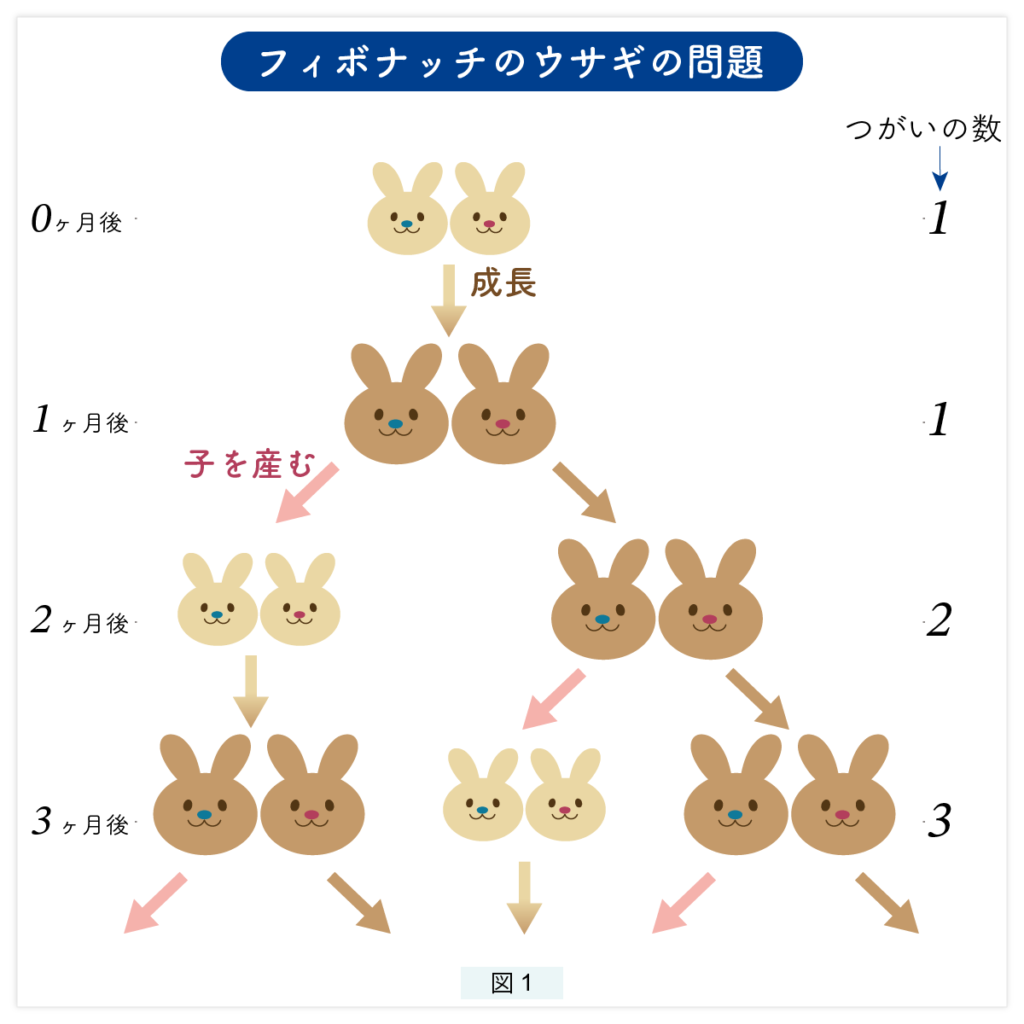
As we track the rabbit population month by month, the numbers naturally follow the sequence:
1, 1, 2, 3, 5, 8… — the Fibonacci sequence (see Figure 1).
In this way, the Fibonacci sequence is more than just a mathematical curiosity.
It also serves as a model for real-world phenomena, such as patterns of growth and reproduction in nature.
What Is the Fibonacci Tree?
he tree structure shown in Figure 2 is known as the Fibonacci tree.
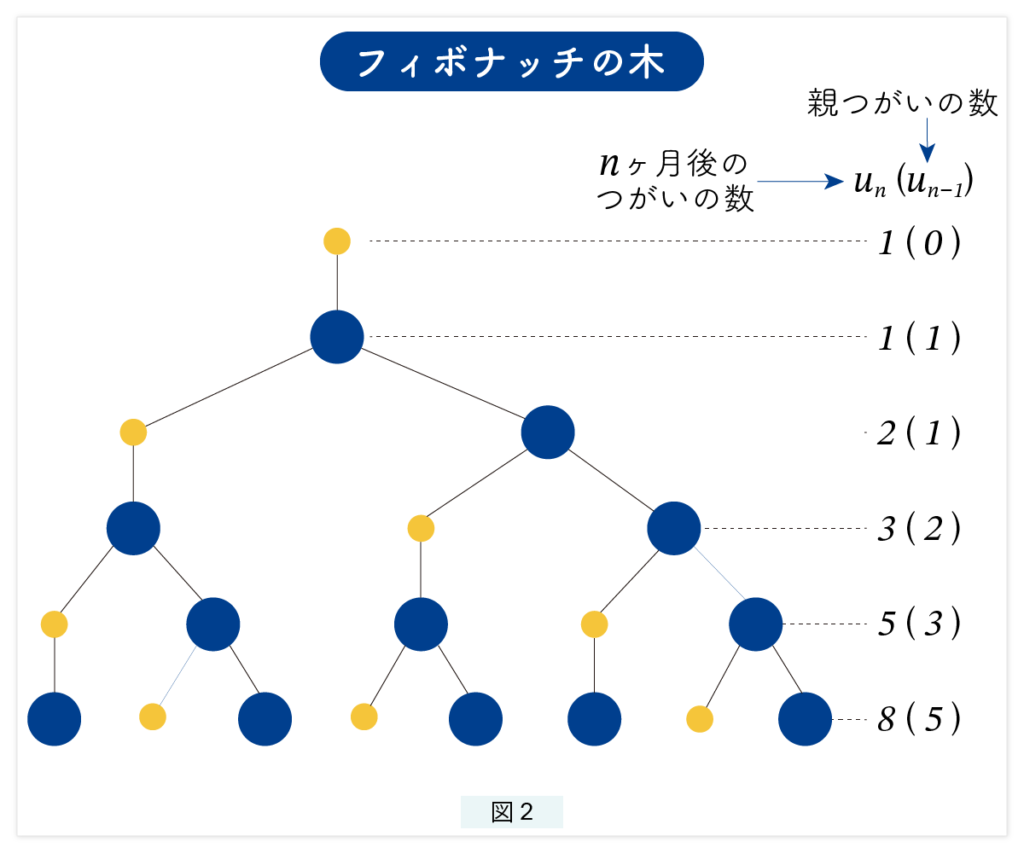
In this diagram:
- The yellow circles represent baby rabbits (one pair)
- The blue circles represent adult rabbits (one pair)
In diagrams like this, the topmost point is called the root.
Interestingly, in mathematics, tree diagrams are typically drawn upside down, with branches expanding from top to bottom. In other words, each node sends its branches downward.
This Fibonacci tree has several noteworthy features:
- Each node (circle) has either one or two branches coming out of it.
- The lowest nodes with no branches are called leaves.
- The root is labeled as Level 0, and as you move downward, the levels are numbered incrementally: Level 1, Level 2, and so on.
The numbers written on the right side of Figure 2 indicate the number of nodes (circles) at each level.
The numbers shown in parentheses represent the number of blue circles (adult rabbit pairs).
Let’s denote the number of nodes at level n as uₙ.
Then, the sequence u₀, u₁, u₂, … follows the Fibonacci sequence we discussed earlier.
Even more interestingly, the number of blue circles (adult rabbits) in parentheses also forms a Fibonacci sequence.
The Recurrence Relation of the Fibonacci Sequence
Let’s take another look at the Fibonacci tree in Figure 2.
At level n, uₙ represents the total number of rabbit pairs after n months,
and uₙ₋₁ represents the number of adult rabbit pairs.
Therefore, the number of newborn rabbit pairs in month n is uₙ − uₙ₋₁.
Since only adult rabbits (uₙ₋₁) give birth, the total number of rabbit pairs in the next month (n + 1) is:
adding the newborns from the adults:
uₙ₊₁ = uₙ + uₙ₋₁
This leads to the following recurrence relation:
In other words, the Fibonacci sequence follows the rule that “each term is the sum of the two preceding terms.”
Definition and Extension of the Fibonacci Sequence
The original Fibonacci sequence, as defined by Fibonacci himself, is:
1, 2, 3, 5, 8, …
Originally, Fibonacci defined the sequence in the form:
1, 2, 3, 5, 8, …
However, the now widely known version with an initial 1 added in front is:
1, 1, 2, 3, 5, 8, …
In more recent times, another version has become common, beginning with 0:
0, 1, 1, 2, 3, 5, …
In general, the Fibonacci sequence can be expressed using the following recurrence relation:
u₁ = 1, u₂ = 1, uₙ₊₁ = uₙ + uₙ₋₁ (for n = 2, 3, 4, …)
The Fibonacci Sequence in Nature
The Fibonacci sequence appears not only in mathematical problems, but also throughout the natural world.
One reason for this is thought to be the concept of self-similarity—a process in which growing structures repeat forms that resemble earlier ones.
Through this self-replicating pattern, nature is believed to use information and energy efficiently, giving rise to the orderly and beautiful structures we observe around us.
The Golden Ratio and the Fibonacci Sequence
The Fibonacci sequence has another fascinating property:
The ratio between two consecutive terms — that is, uₙ₊₁ ÷ uₙ — gradually approaches a special number.
That number is the golden ratio (φ).
For example, consider the following ratios:
2 ÷ 1 = 2.0
3 ÷ 2 = 1.5
5 ÷ 3 ≈ 1.666…
8 ÷ 5 = 1.6
13 ÷ 8 ≈ 1.625
…
As n increases, the ratio approaches the golden ratio φ ≈ 1.618…
The golden ratio is often considered the most aesthetically pleasing proportion to the human eye.
It appears in architecture and art—from the Great Pyramid and the Parthenon, to Renaissance paintings and even modern logo design.
The relationship between the Fibonacci sequence and the golden ratio has long fascinated mathematicians throughout history.
For a deeper look at the golden ratio, we invite you to read a separate article dedicated to that topic.
Conclusion
The Fibonacci sequence is not merely a mathematical curiosity—it is a profound pattern that appears repeatedly in nature, art, and design.
Underlying this recurrence are natural principles such as self-similarity and optimized growth.
The property in which the ratio of consecutive terms approaches the golden ratio only adds to the sequence’s beauty and mystery.
Perhaps the wonders of numbers like these are quietly hidden in our everyday lives.
It may be enjoyable to look for the rhythms of the Fibonacci sequence or the golden ratio in the natural forms and designs that surround us.

