Egyptian Fraction Notation and the Eye of Horus
When discussing ancient science, it is important to avoid projecting modern concepts onto the past and instead use only the technologies and ideas available at the time. In mathematics, the most fundamental concept is the idea of “number.” However, the concept of numbers in ancient times was quite different from what it is today. In Europe, even into the early modern period, “numbers” referred almost exclusively to natural numbers. Fractions and decimals — and even the concept of zero — were unknown.
Today, most people grow up familiar with numbers from an early age and may assume that negative numbers, decimals, and fractions have always existed naturally. But because the concept of numbers is so basic to us now, it can be difficult to imagine a time when these ideas were unfamiliar. Still, let us try to put ourselves in the mindset of the ancients and consider how they understood fractions.
Fractions are a way to measure quantities smaller than the smallest standard unit. If a quantity cannot be measured by the smallest unit, people would use terms like “half” (1/2), and for smaller parts, “half of a half” (1/4). Almost every language in the world has a word for “half” to represent 1/2. In Japan, for example, half of one ryō (a unit of currency) was called “nibu-kin” (二分金), and 1/4 was called “shibu-kin” (四分金).
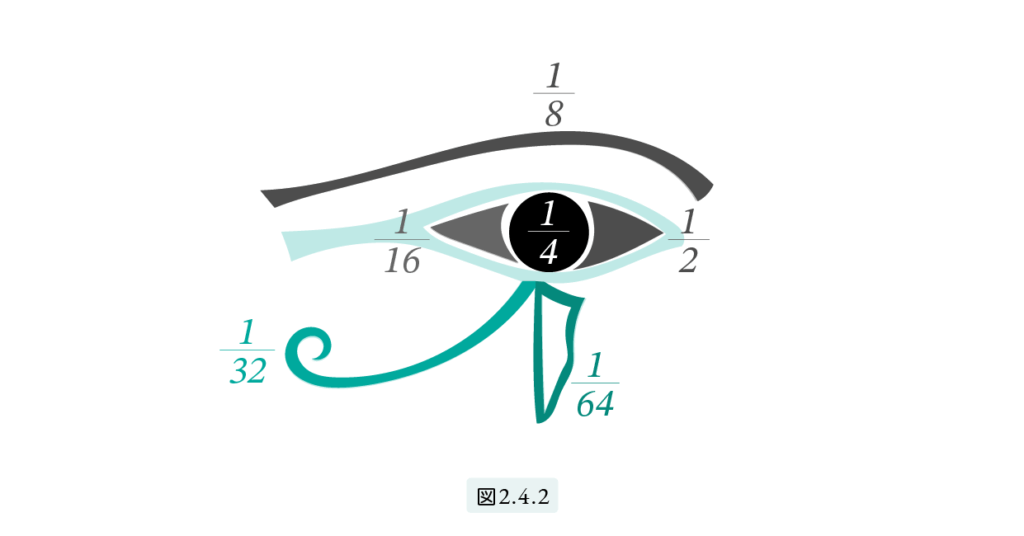
As mentioned in Section 2-4: The Myth of Osiris, the ancient Egyptians had six symbols representing the fractions:
\[\frac{1}{2},\ \frac{1}{4},\ \frac{1}{8},\ \frac{1}{16},\ \frac{1}{32},\ \frac{1}{64}\]
(See also “Eye of Horus” in Figure 2.4.2.)
×
Binary Fractions and Binary Decimals
Modern computers use the binary system. Let’s now take a moment to explore binary fractions. From here on, we are no longer dealing with ancient mathematics but rather modern mathematical concepts. Let us extend the “Eye of Horus” sequence (1) infinitely as follows:
From this sequence (3), we define a binary fraction as any finite combination of these elements, where no term is repeated more than once. For example:
is a binary fraction. Binary fractions can be converted into binary decimals in the following manner.
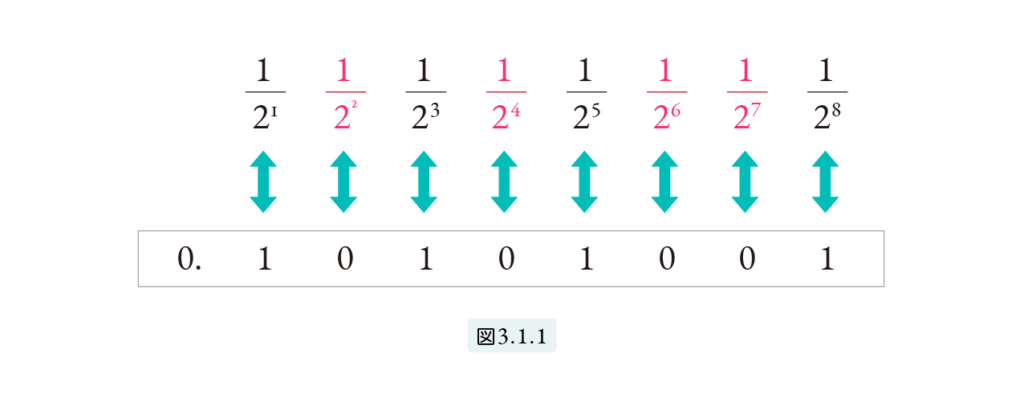
In Figure 3.1.1, the red-colored terms represent the fractions that are not included. If the fraction \(\frac{1}{2^n}\) appears, we assign a 1 to the nth digit; if it does not appear, we assign a 0. In this way, the binary fraction in equation (4) can be converted into the binary decimal:
The reverse conversion works the same way: if the nth digit of a binary decimal is 1, then include \(\frac{1}{2^n}\); if it is 0, do not include it.
Egyptian Fractions
In solving practical problems, using finite binary (or decimal) fractions is sufficient. Today’s computers also only handle finite binary numbers. However, mathematical constants like π = 3.14… or the golden ratio φ = 1.618… cannot be expressed using finite decimals. In order to formulate mathematics as a beautiful and unified system, it was necessary to go beyond finite representations and enter the world of the infinite.
The ancient Egyptians, however, were not satisfied with binary fractions. This is likely because most fractions such as \(\frac{1}{3}\), \(\frac{1}{5}\), and so on, cannot be represented using binary fractions. Instead, they expanded their system to include what are now called “Egyptian fractions.”
A unit fraction is a fraction with 1 as its numerator and a natural number as its denominator. An Egyptian fraction is a sequence of a natural number followed by one or more unit fractions. When there are two or more components, semicolons ( ; ) are used as separators. The rule is that at most one natural number is allowed, and no unit fraction may appear more than once. For example:
are valid Egyptian fractions, while
is not, because the same unit fraction \(\frac{1}{4}\) appears more than once. Including a single natural number in Egyptian fractions is a modern convention, allowing for consistent expressions like “arithmetic operations on Egyptian fractions.”
In ancient times, unit fractions were the foundation of fractional notation across many cultures. In modern Japanese, the fraction \(\frac{m}{n}\) is read as “n-bun no m,” which literally means “m parts of a one-divided-by-n.” The phrase “n-bun” refers to one of n equal parts—i.e., a unit fraction. Therefore, “n-bun no m” means “m copies of one n-th part.”
Egyptian Fractions
In solving practical problems, using finite binary (or decimal) numbers is sufficient. Today’s computers only handle finite binary numbers. However, constants like π = 3.14… and the golden ratio φ = 1.618… cannot be expressed with finite decimals. In order to formulate mathematics as a beautiful and consistent system, it was necessary to go beyond finite representations and explore the infinite.
The ancient Egyptians, however, were not satisfied with binary fractions alone. This is because most fractions, such as \(\frac{1}{3}\) and \(\frac{1}{5}\), cannot be represented exactly using binary fractions. Therefore, they expanded their system into what we now call Egyptian fractions.
A unit fraction is a fraction with a numerator of 1 and a natural number as the denominator. An Egyptian fraction is a sequence consisting of at most one natural number followed by one or more unit fractions. If there are two or more components, semicolons ( ; ) are used as separators. Additionally, the same unit fraction cannot appear more than once. For example:
are valid Egyptian fractions, while
is not, because the same unit fraction \(\frac{1}{4}\) appears twice.
Including a single natural number as part of Egyptian fractions is a modern approach. This allows for a unified discussion, such as “arithmetic operations on Egyptian fractions,” treating both natural numbers and fractional expressions in the same system.
In ancient times, unit fractions were the foundation of fractional expressions everywhere. Even today, in Japanese, the fraction \(\frac{m}{n}\) is called “n-bun no m,” which literally means “m parts of one n-th division.” The “n-bun” refers to one of n equal parts—that is, a unit fraction. Thus, “n-bun no m” means “m copies of a 1/n part.”
Concrete Example of Egyptian Fractions: Dividing 2 Pies Among 7 People
Egyptian fractions are less convenient and have more shortcomings compared to modern fractions. However, there were good reasons for their use. Let’s consider an example: dividing 2 pies among 7 people. The fraction \(\frac{2}{7}\) has a numerator of 2, so it is not an Egyptian fraction. We can convert it into an Egyptian fraction as follows:
If each of the two pies is divided into 4 parts, we obtain 8 pieces of \(\frac{1}{4}\) pies. Distributing 7 of them to 7 people, we have one \(\frac{1}{4}\) piece left. Dividing this remaining piece into 7 equal parts produces 7 pieces of \(\frac{1}{28}\) pies. Thus, each person’s share is \(\frac{1}{4}\) plus \(\frac{1}{28}\).
In general, fractions like \(\frac{2}{7}\) are difficult to grasp intuitively because they are not unit fractions. However, \(\frac{1}{4}\) is a unit fraction and easy to understand intuitively. Therefore, \(\frac{2}{7}\) is approximately \(\frac{1}{4}\) plus a small additional piece, \(\frac{1}{28}\).
In this series, we will not go into the detailed theory of Egyptian fractions. However, it is important to know that the Egyptians were capable of solving complex computational and practical problems almost at the same level as we handle fractions today.
Binary fractions were expressed using parts of the “Eye of Horus.” So, how did the Egyptians represent general Egyptian fractions? Before discussing that, let’s first take a look at how natural numbers were expressed. Although the Egyptian fraction system was a very advanced numerical system for ancient times, the progress in antiquity was extremely gradual. It likely took hundreds of years from the first appearance of numbers to the development of Egyptian fractions.
Egyptian Fractions: Representation Using the Eye of Horus
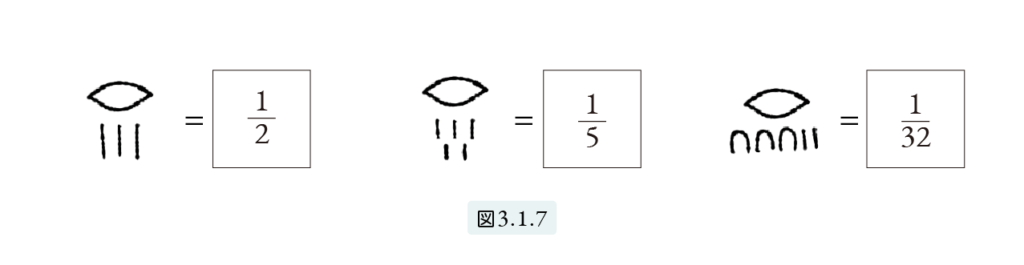
A unit fraction \(\frac{1}{n}\) was represented by writing the symbol of the “Eye of Horus” above the numeral indicating \(n\). For example, \(\frac{1}{3}\), \(\frac{1}{5}\), and \(\frac{1}{32}\) were depicted as shown in Figure 3.1.7.
One possible reason why Egyptian fractions remained as they were, without developing into the fractional notation we use today, may be due to this particular method of writing.
The Recognition of Natural Numbers as Abstract Concepts
Natural numbers representing quantities gradually came to be recognized as abstract entities, independent from the objects being counted. For example, in Figure 3.1.6, the numbers represented by the Egyptians correspond to the same number we imagine today as 2,123,013. What these notations express is not tied to specific objects (such as sheep or jars) but rather to an abstract concept called “natural numbers.”
Then, how were quantities other than counts—such as length, area, volume, and angle—perceived? Since it is difficult to know precisely how ancient people perceived them, we will focus only on the observable phenomena.
Units of Length in Ancient Egypt: Cubit, Palm, and Digit
Let’s review the units of length used in ancient Egypt.
As mentioned in 1-3. The Mystery of the Pyramids and Those Fascinated by It, length was expressed in the following units:
1 cubit = 7 palms, and
1 palm = 4 digits.
Here, the numbers 1, 4, and 7 are written using modern numerals, but in ancient Egypt, they would have been written in Egyptian numerals.
For example, a certain length could be expressed as:
2 cubits, 5 palms, and 3 digits. (4)
Originally, a cubit referred to the length of a forearm, a palm referred to the width of a hand, and a digit referred to the width of a finger.
Thus, (4) would mean “the length of two forearms, five palms, and three fingers.”
However, over time, these measurements evolved into standardized units.
In ancient Egypt, a unit word only made sense when combined with a numeral, and the concept of separating numbers and units did not exist.
The Concept of Quantities as Numbers with Units
Alongside “numbers,” there is the concept of “quantities.”
Even today, quantities are widely used in fields like physics, but as with numbers, their meaning can vary depending on the era or individual.
In this series, we define:
A quantity is a number with a unit.
For example, these are quantities:
3 days, 3 people, 3.14 grams, 22 7 meters.
The term “number” refers to the numbers you are familiar with today, including decimals and fractions.
When dealing with quantities, only those of the same type can be added together.
For example, weight (grams) and length (meters) cannot be added.
When considering quantities other than the number of objects in ancient times—such as length, area, volume, weight, or angles—it is helpful to interpret them through this concept of “quantities.”
This concept is very useful for performing calculations involving different units.
Now, let’s try a practice problem based on the addition of Egyptian units of length:
3 cubits 4 palms 1 digit
- 2 cubits 5 palms 3 digits = 5 cubits 9 palms 4 digits = 6 cubits 3 palms.
To convert cubits to palms, multiply by 7.
To convert palms to cubits, divide by 7.
Thus:
6 cubits 2 palms = 44 palms = 6;2/7 cubits.
The Application of Modern Mathematics to Angles and Pyramid Analysis
Next, let’s talk about angles.
The unit of angle measurement where a full circle is divided into 360 degrees was already used in Babylonia, but it is believed that this system had not yet been introduced to Egypt during the Old Kingdom period.
Therefore, whenever this series uses degrees to express angles, please understand that it is applying concepts from modern mathematics.
Later, when analyzing the inclination angles of pyramids, we will also use modern mathematical methods based on this degree system.
Units Smaller than One Degree: Minutes and Seconds
For units smaller than one degree, we use minutes and seconds.
- 1 minute = \[\frac{1}{60}\] of a degree
- 1 second = \[\frac{1}{60}\] of a minute
When converting degrees to minutes, multiply by 60.
When converting minutes to seconds, also multiply by 60.
Example:
\[3^\circ 4′ = 3 \times 60 + 4 = 184\] minutes
\[3^\circ 4′ 5” = 184\] minutes 5 seconds
\[= 184 \times 60 + 5 = 11045\] seconds
When converting seconds back to minutes, divide by 60.
When converting minutes back to degrees, also divide by 60.
Sometimes, decimals are used instead of fractions.
Unless otherwise noted, decimal points in this text represent base-10 (decimal) notation.
Example:
\[3^\circ 4′ 5” = 3^\circ \left(4 + \frac{5}{60}\right)’ = 3 + \left(4 + \frac{5}{60}\right) \times \frac{1}{60}^\circ = 3.06855\ldots^\circ\]
To convert from decimal degrees back to degrees, minutes, and seconds, use the process of “converting degrees to minutes and minutes to seconds” described above.
Example:
\[3.068055^\circ = 3^\circ 0.068055^\circ = 3^\circ 0.068055 \times 60′ = 3^\circ 4.0833′ = 3^\circ 4′ 0.0833′ = 3^\circ 4′ 0.0833 \times 60” = 3^\circ 4′ 4.998”\]
Since we truncated the repeating decimal portion (the “…” part) in the earlier calculation, the final answer does not match exactly, but it closely approximates the original value.
Summary
Today, we naturally treat quantities such as length and weight as numerical values, using a single standard unit name for each type—for example, meters for length and grams for weight. Therefore, we have no resistance to thinking of quantities with a simple structure like “quantity = number + unit,” as explained earlier.
However, in ancient Egypt, lengths were expressed as a sum of different units such as cubits, palms, and digits. Furthermore, the “carrying over” between units (from digits to palms, and palms to cubits) was not based on the decimal system.
Such practices may have prevented the Egyptians from perceiving quantities as just another form of number.

