In this article, we explore how people in ancient times perceived the “Mystery of the Pyramids.”
Ancient Civilizations and Plato’s Atlantis Legend
In ancient times, the world was believed to be inhabited by gods and mythical creatures. Beyond the stars, gods were thought to dwell, and at the edge of the Earth, one-eyed giants roamed. Today, with countless galaxies mapped across the cosmos and every corner of the Earth explored, there’s no longer room for gods to reside—nor places for giants to hide. Have the gods simply given way to extraterrestrial beings?
Since ancient times, humanity has been captivated by mysterious stories. How did people in antiquity pass down tales of the ancient Egyptian civilization?
The Great Pyramid of Khufu has fascinated countless visitors for centuries. In an era without modern skyscrapers, those who stood before this immense structure were surely overwhelmed, wondering how such a thing could have been built by humans. Many must have believed it to be the work of gods. Some imagined that within the pyramid lay treasures of immense value—magical weapons bestowed by deities, potions with mysterious powers, or sacred scrolls containing divine revelations. Indeed, stories of hidden maps, secret spells, and ancient prophecies are often associated with temples and ruins of old.
In Chapter 1-1, “What is the Mystery of the Pyramids?”, we briefly touched on one interpretation: the Ancient Advanced Civilization Theory, which claims that a highly developed civilization existed long before even ancient Greece. This idea finds its roots in the famous Atlantis legend, found in Plato’s dialogue Critias.
The name Critias comes from Plato’s great-grandfather, to whom Plato attributes the tale of a noble, early Athens. Critias reportedly heard this story from his relative Solon, a renowned Athenian lawmaker and philosopher. Solon, during his travels in Egypt, was told the story by local priests. Plato introduces the tale with the implication: “This isn’t a myth—this is what the Egyptian priests told Solon, so it’s credible.”
In those days, Egypt was a highly advanced civilization, while Greece was still developing. Many Greek thinkers traveled to Egypt to learn about politics, science, and culture. What the Egyptian priests told Solon was the following:
The Atlantis Legend
Egypt, they said, had a history stretching back 8,000 years. But even 9,000 years before that, a utopian civilization had flourished in ancient Athens. The city was ruled by philosopher-kings and noble warriors who governed with wisdom and justice. They lived simply, cared little for wealth, and valued philosophy above all.
At the time, the Greek world was threatened by the expanding Atlantis Empire, ruled by the descendants of Atlas, son of the sea god Poseidon. Atlantis was said to lie beyond the Pillars of Hercules (the modern Strait of Gibraltar) in the vast ocean—a land that would one day be known as the Atlantic, named after Atlas himself.
Athens formed a coalition of allies and fought against Atlantis. Though noble, Atlantis was ultimately corrupted by its growing power. As the saying goes, “evil never prospers”: Atlantis was punished by the gods and sank into the sea in a single night, swallowed by a great tsunami.
This is a very rough summary of Plato’s Atlantis legend. The tale reads like an ancient version of Star Wars—bold and imaginative. But many believe Plato’s true purpose was to provoke thought about the ideal state, and Atlantis served only as a backdrop to engage the reader.
Still, one can’t help but wonder if Plato simply enjoyed telling a good story.
Plato lived at the end of Greece’s Classical Period, a time when many Greek philosophers, including Plato himself, journeyed to Egypt in pursuit of wisdom. Some historians even refer to this intellectual pilgrimage as the “Egyptian Pilgrimage.”
As discussed in Chapter 1-1, Herodotus, known as the “Father of History,” also visited Egypt during this period and documented its customs and culture in vivid detail. In modern writings about the pyramids, one often encounters references to the “Herodotus Manuscript,” supposedly revealing pyramid secrets. But in truth, Herodotus never wrote about any pyramid mystery. Either his work was misunderstood, or later writings were simply fabrications.
The Hellenistic Era: Alexandria Becomes the Cultural Epicenter
The Late Classical Period and the Rise of Hellenism: From Athens to Alexandria
Toward the end of Greece’s Classical period, city-states across the region were embroiled in constant conflict. Historians often refer to this era as the time of civil wars. Eventually, a small kingdom in the north—Macedonia—rose to power and defeated the Greek city-state alliances, ushering in the Hellenistic Era.
With this shift, the cultural center of the ancient world moved from Athens in mainland Greece to Alexandria, the capital of Egypt’s Ptolemaic dynasty. Egypt, once ruled by native pharaohs, was now governed by foreign rulers—Greeks by culture, Macedonians by origin.
Alexandria became a true cosmopolis, a global city. It was home to native Egyptians and Greeks alike, as well as people from across the Mediterranean islands, West Asia, and even as far as India and the northern shores of the Black Sea. Its multicultural atmosphere was unmatched in the ancient world.
It was in Alexandria that the Mouseion, a royal research institute, was founded—along with its legendary Library of Alexandria, which would become the most famous repository of knowledge in antiquity.
While literature and the arts are often said to have declined during the Hellenistic period, science—especially astronomy and mathematics—thrived. Research in these fields required institutional support akin to modern universities, and Alexandria provided exactly that.
Great minds like Archimedes, and Euclid, the author of Elements, lived and worked during this time—pushing the boundaries of knowledge in ways that continue to influence us today.
The Rise of Rome and the Fate of Greek Mathematics
Eventually, Egypt fell to Rome, and the Orient came under Roman control. While Athens lost much of its political and economic power, it survived as a city of learning, particularly in philosophy. It became a popular destination for the sons of Roman aristocrats seeking an elite education.
Egypt, meanwhile, became a crucial breadbasket for the Roman Empire, and Alexandria—especially its scientific research center, the Mouseion—continued to operate with support from the imperial government.
Rome, the city, amassed vast wealth and embarked on a spree of monumental construction: grand arenas, aqueducts, temples, and more. Yet in terms of culture, it lagged behind the East. The cultural heart of the empire remained firmly in the eastern Mediterranean.
It was in this region that Christianity emerged and gradually grew in influence. Greek philosophy, which had long carried a spiritual tone, began to clash with Christian doctrine. Since mathematics was considered a branch of philosophy, the decline in the status of Greek philosophy also affected the perception of mathematics. Ongoing research relied on continued Roman patronage, and some of the more celebratory stories about the brilliance of Greek mathematics appear to have been crafted during this time to justify such support.
One rhetorical strategy was to elevate Greek civilization by contrasting it with a “primitive” Egypt. Many writers of the period—such as Strabo, Plutarch, Diodorus, and Pliny the Elder—wrote rather critically of Egypt. A particular target was Herodotus, who had praised Egyptian culture in his Histories. Critics accused him of being overly fond of “barbarians.”
Plutarch, in particular, wrote an entire essay titled On the Malice of Herodotus, listing the so-called offenses of the historian. As a result, Herodotus’ reputation has fluctuated wildly throughout history. When Egypt is viewed favorably, Herodotus is praised; when Egypt falls out of favor, Herodotus’ standing declines as well.
The Rise of Arabic (Islamic) Mathematics
After the division of the Roman Empire into East and West, the Western Roman Empire—centered on the Italian Peninsula—was effectively severed from the Orient. As a result, Western Europe entered what is often called the Dark Ages of the Middle Ages. The Eastern Roman Empire, however, based in Anatolia (modern-day Turkey), continued to exist for nearly a thousand years, surviving until the mid-15th century.
Meanwhile, Islam, founded by the Prophet Muhammad in the Arabian Peninsula, rapidly spread across the Orient, and Egypt became part of the Islamic world. It was in this context that Caliph al-Ma’mun emerged—a ruler known for his passionate support of science and the arts. He sought to absorb the vast body of knowledge that had been preserved in cities like Alexandria, which had long been a center of learning.
At the time, much of the scholarly knowledge in the Orient was written in Greek, and under al-Ma’mun’s patronage, these works were systematically translated into Arabic. The body of knowledge that developed during this period came to be known as Arabic mathematics or Islamic mathematics. In this way, Greek mathematics found a new home and legacy within the Islamic world.
Al-Ma’mun was also deeply interested in ancient texts handed down through the Orient. In Babylonia, astrology and astronomy had flourished, and many ancient documents recorded detailed star charts along with the events that occurred under certain celestial alignments—used as tools of divination. Al-Ma’mun and his scholars believed that among these texts might be clues to uncovering the underlying laws of the universe.
According to Arabic sources, in 820 CE, al-Ma’mun led an expedition to Giza, accompanied by a team of stonemasons and engineers. Today, there is a tunnel that cuts into the Great Pyramid, often referred to as a “robber’s passage.” It is believed that this tunnel was created under al-Ma’mun’s orders.
While it’s likely that the expedition hoped to discover gold and treasure, some accounts claim a different motive: legends spoke of a secret chamber within the pyramid containing items such as a “rust-proof weapon,” glass that would not break even when bent, and maps of the Earth and the heavens. Given al-Ma’mun’s deep interest in astronomy and mathematics, it is entirely possible that what truly captivated him was not treasure, but the pursuit of ancient knowledge and unsolved mysteries.
The Renaissance Revival of Ancient Civilizations and the Evolution of Knowledge
Western Europe gradually emerged from the cultural stagnation of the so-called Dark Ages and entered the Renaissance—a period defined by a revival of classical antiquity, particularly the civilizations of Greece and Rome. Yet, during this time, interest in ancient Egyptian civilization also experienced a notable resurgence.
In fact, rather than focusing solely on the rational philosophies of thinkers like Plato and Aristotle, many Renaissance minds were drawn to the mystical and arcane traditions of the Orient: astrology, magic, alchemy, and other esoteric systems. While modern readers may dismiss these as “unscientific” or “superstitions,” people in both ancient times and the Renaissance were not indifferent to rational inquiry or the pursuit of cause and effect.
Instead, as knowledge expanded, so did the understanding of natural phenomena. Over time, astrology evolved into astronomy, alchemy gave rise to chemistry, magic was transformed into medicine, and numerology contributed to the development of mathematics. What once seemed mysterious or supernatural gradually became part of the scientific worldview.
The Revival of Neoplatonism and the Mystery of the Pyramids
In the 15th century, the philosopher Marsilio Ficino played a central role in reviving Neoplatonism. Among his most notable achievements was his translation of the Hermetic Corpus, a set of mystical writings believed to originate from antiquity. The figure of Hermes Trismegistus, to whom these texts were attributed, was said to be a sage and magician in ancient Alexandria—one who could travel between the world of the living and the afterlife, and who possessed ancient wisdom and magical powers. By the 3rd century CE, he was revered as a reincarnation of the Egyptian god Thoth.
Ficino worked under the patronage of Cosimo de’ Medici, a powerful Florentine ruler and a devoted supporter of the arts. Interestingly, Cosimo instructed Ficino to translate the Hermetic texts before even translating Plato’s Republic—a decision that reflects the era’s deep fascination with mystical and esoteric knowledge, especially that which was thought to originate in ancient Egypt.
During this period, the name Pythagoras appeared frequently in writings. He was often credited—rightly or not—with bold ideas such as “the Earth is a sphere” or “the sun is made of fire.” Some even attributed to him the theory discussed in Chapter 1-1: The Mystery of the Pyramids—that the Great Pyramid was constructed to encode the circumference of the Earth. Many of these claims were likely legends or inventions of later generations, reflecting the Renaissance tendency to project their ideals onto figures of the ancient world.
Even the renowned polymath Leonardo da Vinci expressed great admiration for ancient Egyptian knowledge. He once wrote:

“The ancient Egyptians created accurate maps of the world using latitude and longitude, and they used meridians and angles to study the stars with extraordinary precision. We should study their astronomy.”
Though Leonardo did not receive a formal education, he taught himself mathematics and geometry, and after meeting the Franciscan friar and mathematician Luca Pacioli, he dove deeply into Greek geometry and Arabic mathematics. His famous explorations of the golden ratio are discussed in Chapters 3 and 4.
Across Europe, the Renaissance fascination with Egyptian astrology, magic, and mystery was widespread. The most esoteric aspects of these practices were often merged with Platonic philosophy, giving rise to the widespread appeal of Neoplatonism.
This was also the Age of Exploration, when rare objects and ideas flowed into Europe from all corners of the globe. Sciences like astronomy and geography advanced rapidly, yet many people still felt their knowledge was incomplete. The Italian scientist and mathematician Gerolamo Cardano, based in Milan, lamented:

“The Greeks transmitted only an incomplete version of the Egyptians’ methods of calculation.”
The desire to reclaim the lost wisdom of the ancients was partly driven by mystical curiosity, but also by a very practical ambition: to acquire useful, applicable knowledge.
Although no writings from the Renaissance explicitly refer to the “mystery of the pyramids” as we frame it today, traditions related to the size of the Earth—and the ancient maps that supposedly encoded it—were often linked to the pyramids in historical memory.
Those Captivated by the Mystery of the Pyramids
By the 17th century, Europe had moved beyond the Age of Exploration and entered what historians now call the Scientific Revolution—a period marked by rapid advancements in science, including mathematics. At the time, Egypt was part of the Islamic world, ruled by the Ottoman Empire, and to many Europeans, it remained a land shrouded in mystery, filled with exoticism and non-Christian mysticism.
History books often portray this period as an age when “the dark mists of the Middle Ages began to clear,” and people freed themselves from superstition and magical worldviews. It’s said that they began to think rationally, no longer attributing everything to an unknowable god, but instead seeking to understand the principles and laws that govern the universe.
However, such portrayals likely reflect the worldview of 19th-century historians, rather than how people at the time actually thought.
There’s no doubt that thinkers like Isaac Newton, Johannes Kepler, and Galileo Galilei gradually transformed people’s views. In the dominant worldview of the time, heaven—the dwelling place of God—was considered a realm governed by laws entirely different from those of the earthly world. But Newton’s discovery of the law of universal gravitation suggested something revolutionary: the same principles that apply to objects on Earth also govern the motion of celestial bodies.
Today, we interpret this to mean that the universe is not driven by mysterious divine forces, but by mathematical laws, such as those describing gravitational attraction. However, for Newton himself, this did not contradict the existence of God. On the contrary, he believed that the force of gravity itself was an expression of divine power.
Likewise, the famous quote often attributed to Galileo—that “mathematics is the language of God”—was not meant to secularize science, but rather to suggest that God had used mathematics as the language to design the universe. Galileo himself was a devout Christian and believed that no such beautiful formulas could exist unless they were the work of God.
Kepler, too, was a committed astrologer. His own mother narrowly escaped execution in a witch trial. The complete detachment of science from religion would not come until the 19th century.
At one point in his life, Newton became so absorbed in ancient religious texts, the works of Herodotus, and manuscripts on alchemy, that he temporarily neglected his groundbreaking work in mathematics, physics, and astronomy. After Newton’s death, the economist and scholar John Maynard Keynes, who examined his manuscripts, famously remarked, “Newton was not the first of the age of reason—he was the last of the magicians.”
According to the historian who organized his writings, the bulk of Newton’s handwritten legacy consisted of “terrible and worthless texts.” Newton’s curious connection to the pyramids will be explored in the following section.
John Greaves and the Survey of the Great Pyramid
Even in the 17th century, Egypt’s allure had not faded. In fact, it appears to have been a more popular destination for European travelers than Greece. However, it was during this same century that serious investigations of the pyramids finally began.
One of the earliest and most notable figures to undertake such a study was the English mathematician John Greaves. A true polymath, Greaves was not only well-versed in mathematics and astronomy, but also fluent in Latin, Arabic, Greek, and Persian. He also had a strong interest in archaeology.
Inspired by earlier thinkers like Leonardo da Vinci and Pythagoras, Greaves believed that unlocking the mystery of the Great Pyramid could lead to a better understanding of the true size of the Earth. Equipped with the most advanced surveying instruments available at the time, he traveled to Egypt and carried out a thorough and systematic measurement of the Great Pyramid, both inside and out.
By then, the pyramid already had an opening—now known as the “Robber’s Tunnel”—which allowed access to the interior. Greaves took detailed measurements of nearly every aspect of the structure, and his dedication to precision eventually earned him the nickname “the man who measured everything.”
After returning to England, he was appointed Professor of Astronomy at Oxford University. There, he compiled his findings and published them in a book titled Pyramidographia. The book proved enormously popular—not only among scholars but also among the general public—sparking a wave of fascination with the Great Pyramid across Europe.
However, the task of measurement was far from easy. Much of the base of the pyramid was buried in rubble and debris, making accurate measurements extremely difficult. As a result, some of Greaves’ data included significant margins of error.
Newton’s Research and the Ancient System of Body-Based Measurements
Isaac Newton became deeply intrigued by John Greaves’ work on the pyramids. He believed that by uncovering the ancient units of measurement, one could begin to solve the mysteries of ancient monuments. Motivated by this idea, Newton is said to have studied not only the measurements of Egyptian temples, but also those of other ancient sites around the world.
In ancient times, most systems of measurement were based on body parts, known as anthropometric units. In Egypt, for example, the cubit was defined as the distance from the elbow to the tip of the middle finger. A palm represented the width of the hand, typically measured across four fingers, and a digit was the width of a single finger (see Figure 1.3.1).
Until relatively recently, body-based measurements were used throughout much of the world. In Japan (as well as in China), the traditional unit of length known as the shaku was originally based on the span of an open hand, while the sun (like the digit) corresponded to the width of a finger.
Similarly, in ancient Mesopotamia, Greece, and Rome, units such as the cubit were widely used. However, the length of a cubit varied depending on the region and historical period. It was considered the duty of the king to define and maintain a standardized royal cubit, often using a physical reference rod.
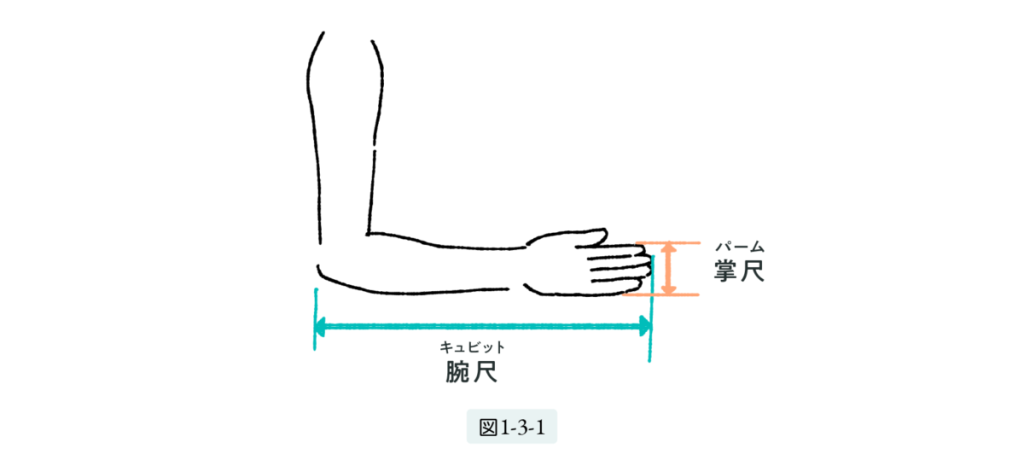
Newton became fascinated by Greaves’ writings on the pyramid. He believed that if one could decode the ancient units of measurement, it might be possible to uncover the secrets of ancient architecture. He even investigated measurement systems used in other ancient temples beyond Egypt.
These ancient systems were anthropometric—based on body parts. For example, in Egypt, the royal cubit was the distance from the fingertips to the elbow, the palm was the width of four fingers, and the digit was the width of a single finger. These units were common not only in Egypt but also in ancient Mesopotamia, Greece, and Rome. The exact length of a cubit varied across time and region, and it was traditionally the king’s role to define the official standard.
Newton theorized that the Great Pyramid was built using these ancient units, and that the dimensions of its inner chambers, such as the King’s Chamber, would yield whole numbers when measured in the correct units. Using Greaves’ recorded measurements, Newton calculated the ratio of the chamber’s length to its width—since ratios are independent of unit systems.
From this, he concluded that the builders must have used two different cubit standards: the standard cubit and the royal cubit. It was a brilliant hypothesis, but unfortunately, Greaves’ data was inaccurate, leading Newton to incorrect results. Based on his calculations, Newton estimated the standard cubit to be about 53 centimeters, and the royal cubit to be around 63 centimeters.
In contrast, modern estimates place the royal cubit of the Old Kingdom at approximately 52.3 to 52.5 centimeters. Newton’s value of 63 cm (about 25 inches) was significantly off, and this miscalculation influenced later interpretations in misleading ways.
Nonetheless, Newton converted Greaves’ pyramid measurements into cubits and concluded that the pyramid had been constructed with deliberate precision. His work was not mystical or pseudoscientific—it was published as a serious academic paper.
Interestingly, Newton’s law of universal gravitation is not directly related to the size of the Earth. Because gravity from large bodies like the Earth can be modeled as if it originates from a single point at the center (a concept known as central force), precise knowledge of Earth’s circumference wasn’t essential for his gravitational theory.
Still, there were rumors at the time that Newton was trying to verify his law of gravity using precise measurements of Earth’s circumference, and that the Great Pyramid’s dimensions might contain this information. While some dismiss this idea, it may not be entirely unfounded.
During the Great Plague of 1665, Newton retreated to his childhood home in the countryside to avoid infection. This period is often referred to as his “Annus Mirabilis” (Year of Wonders), during which he developed the foundations of his three major scientific discoveries. While working on gravitational force calculations, he noticed a discrepancy between his predicted and actual results, leading him to temporarily abandon the project.
The issue stemmed from his use of inaccurate values for Earth’s circumference. Later, in 1679, Newton resumed the calculations using the newly published measurements of Jean Picard, a French astronomer. With Picard’s more accurate data, Newton’s results aligned much more closely with his predictions.
This suggests that Newton had long sought a more precise value for the Earth’s circumference, and it’s quite possible he hoped that the Great Pyramid might hold such information. There’s even a story that Newton believed if one continued calculating the decimal expansion of π, a divine revelation might eventually appear.

